Demystifying the cubic-bezier function ft. JavaScript
 Rishab Raj
Rishab Raj
Introduction
If you are a professional web developer or just getting started then you might have come across the bezier-curve function in our beloved CSS. But have you ever wondered how it works underneath or how we can write that function in JavaScript? Hello👋 developer I am Rishab and I am back with yet another boring blog post and this time about the bezier-curve. So let's get started.
What is the bezier curve?
Bezier curve in computer science is used to draw shapes or to control the flow of animation, which we use to specify the timing function in CSS. It is a curve that can be defined with 2, 3, 4, or more control points, but you might be thinking about how this curve can be used to control the flow of animation?
Components of Curve
For web animations, we use the curve with 4 points and It's easy as depicted in the figure below we have a curve that is drawn in a 2D coordinate system with an initial point, the final point, and two anchor points controlling the curve.
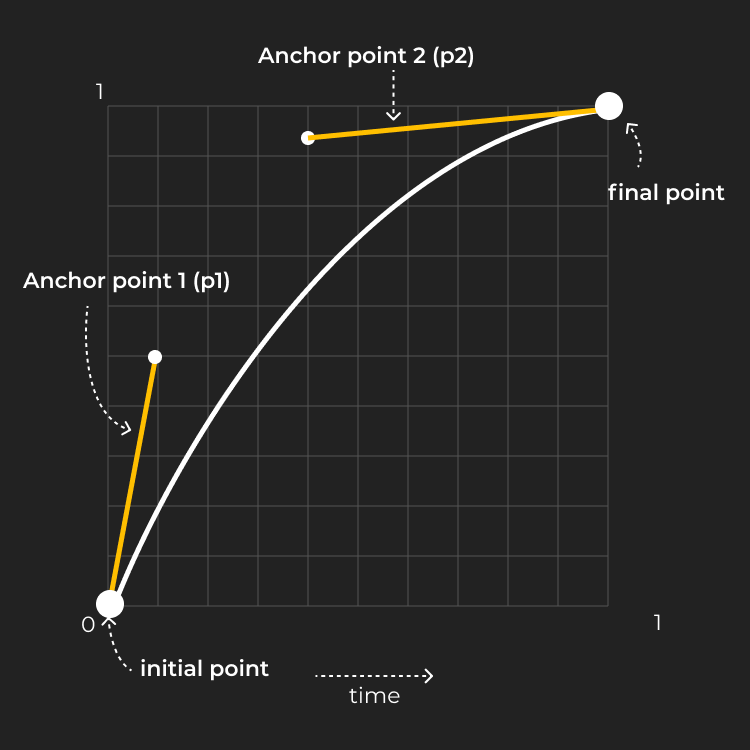
So here as the graph is in normalized form initial point represents the initial value of the animation, the final point represents the final value of our animation but on a scale of 0 to 1. its cubic-bezier function in CSS could be written like cubic-bezier(1, 0, 0,1) where the first two numbers represent the coordinate of the first anchor point and the second 2 coordinates represent the coordinate of the second anchor. The curve represents the value of the animation as it occurs. So we can use this curve to get the value of our animation at a particular instance in normalized form and later change it to the required value.
The JavaScript function
So finally the javascript function you are waiting for
function bezier(t , initial , p1, p2, final){
return (1 - t) * (1 - t) * (1 - t) * initial
+
3 * (1 - t) * (1 - t) * t * p1
+
3 * (1 - t) * t * t * p2
+
t * t * t * final;
}
so this is the functional representation of the formula (1−t)^3*P1 + 3*(1−t)^2*t*P2 +3*(1−t)*t^2*P3 + t^3*P4which takes the time, initial, final, and two anchor points of the curve and gives us the output in the form of the value at that particular instance of time.
Example time🕐
So now let's test our function here we are going to represent a bezier curve which looks like this
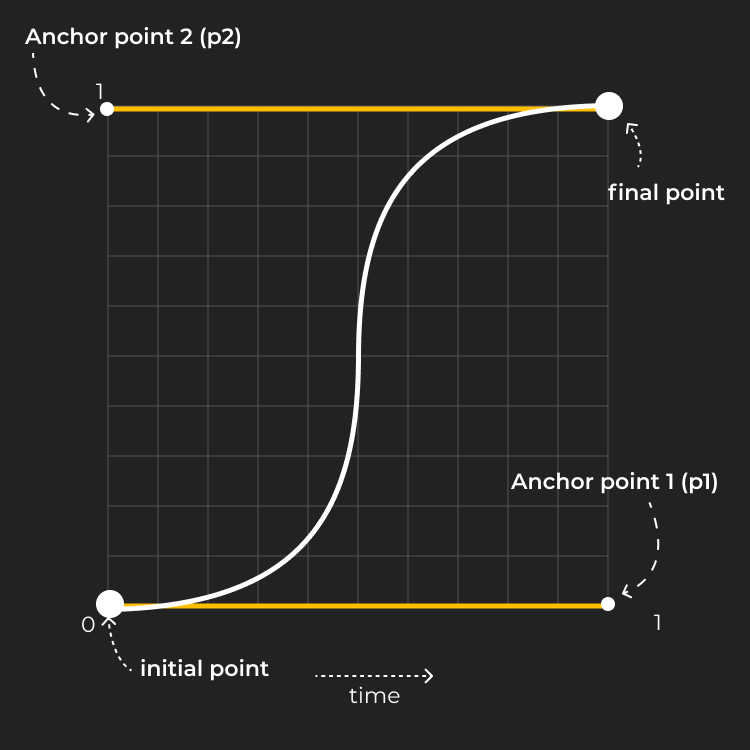
in JavaScript using a function
const obj = document.querySelector(".obj");
let frame;
let totalDuration = 5;
let totalFrame = totalDuration * 60;
let increment = 1 / totalFrame;
let currentTime = 0;
// our beloved bezier function
function bezier(t, initial, p1, p2, final) {
return (
(1 - t) * (1 - t) * (1 - t) * initial +
3 * (1 - t) * (1 - t) * t * p1 +
3 * (1 - t) * t * t * p2 +
t * t * t * final
);
}
function anim() {
if (currentTime * totalDuration >= totalDuration) {
cancelAnimationFrame(frame);
} else {
let currentValue = bezier(
currentTime, // currentTime of the animation
0, // initial Value
// first anchor's x axis coordinate point as shown in the css bezier curve function above, multiplied with <br> final value of get the original value out of normalized form
1 * 500,
// second anchor's x axis coordinate point as shown in the css bezier curve function above, multiplied <br> with final value of get the original value out of normalized form
0 * 500,
500 // final value
);
currentTime += increment;
obj.style.transform = `translateX(${currentValue}px)`;
frame = requestAnimationFrame(anim);
}
}
here as documented in the code we are calling the anim function repeatedly using requestAnimationFrame and in each frame, we are getting the value of our animation using the bezier function by providing it the initial value, final value, instance of the time on which we want the value of the animation and the two anchor points x-axis coordinate multiplied with the final value of the animation to get the value out of normalized form
and that's it, we have created our own cubic-bezier function in JavaScript.
Here is the full example in codepen which you can use to play around
Thank you for reading the post and if you like it make sure to give it a thumbs up. If you are looking for a freelance web developer then visit my profile
Subscribe to my newsletter
Read articles from Rishab Raj directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Rishab Raj
Rishab Raj
I am a developer who loves to share his learning with others