Reverse geocode cities from geographic coordinates

Reverse geocode is used to convert latitude-longitude coordinates to a list of locations, which can then be used in search results.

In many consumer applications, the search experience is one of the most important aspects of consumer satisfaction. Search usually comes in these forms:

• Pre-defined search tags(e.g. cuisine, location)
• Free-text fields
• Map

Also, there are a wide variety of filters to refine the results.

Introduction

In this post, I will be sharing the approach I used to implement the feature to reverse geocode in map search and match it against a pre-defined list of locations. This is one of the more interesting features that I did as part of my work.

For this example, let's use New Zealand as the place of interest, with its cities as the search locations.

There was nothing out of the ordinary when I was working on this feature. All I need are the list of pre-defined locations, input coordinates, and a way to check whether a point is inside a polygon.

Within a short period of time, this feature was developed, tested, and pushed to production.

After a few days, I decided to play around with the feature on the mobile application, trying out various zoom levels to make sure that the app is able to receive the expected locations.

Unfortunately, no locations were returned when the map is zoomed out far enough to show the entire New Zealand area. But, when the map is zoomed in a little, the reverse geocode feature returns the expected locations.

I was confused, and don't know why this happened. But I guess it must be because of the boundary of the map.

So, I looked up the longitude and latitude markings on the world map and indeed, New Zealand is right next to the longitude boundary, where the longitude becomes negative as it crosses over to the Americas.

To confirm, I logged out the coordinates of the northeast and southwest bounding box, which showed that the longitude of the northeast point is negative and the longitude of the southwest point is positive. This confirmed my hypothesis.

New Zealand and the longitude boundary on its right, where it becomes negative

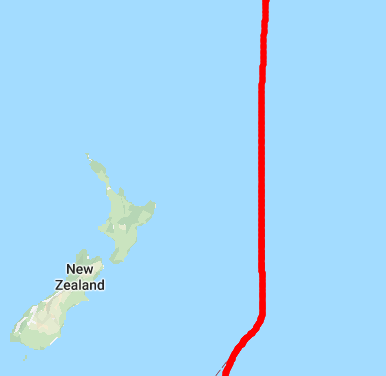
Therefore, there are three edge cases to take care of:

1. When longitude crosses over
2. When latitude crosses over
3. When longitude and latitude crosses over

Preparation

Here are the data that we need to prepare beforehand:

• A list of pre-defined locations that we want to support(Can be from a database, internal service, etc)
• Polygon points(list of latitude-longitude pairs) for every location

Fig 1. For Auckland, I mark out the polygon sides and take note of the latitude-longitude pairs.

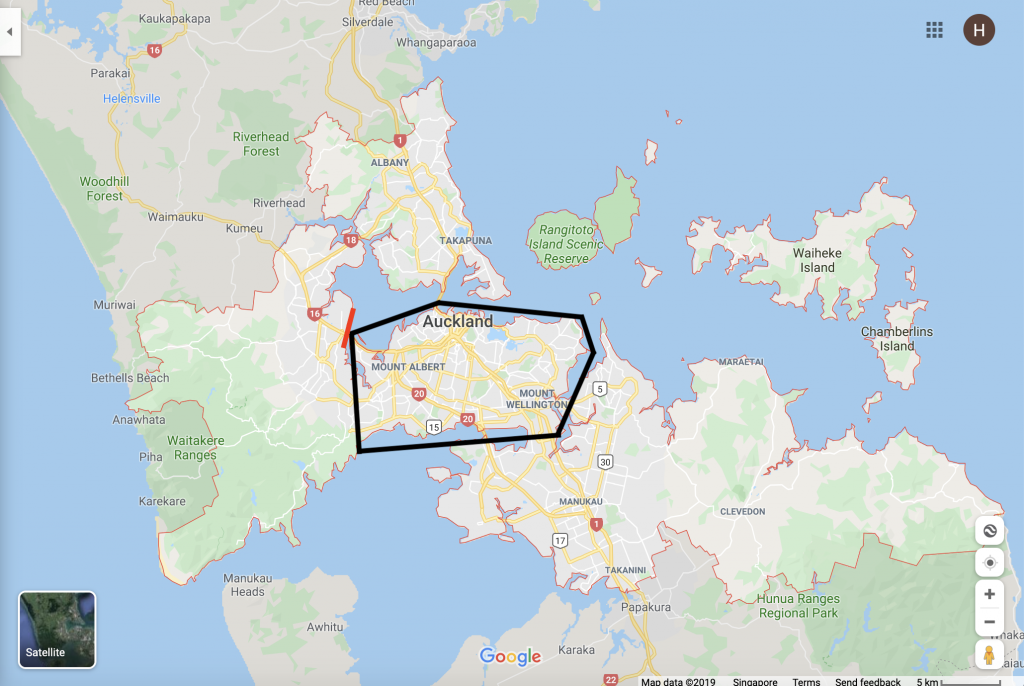
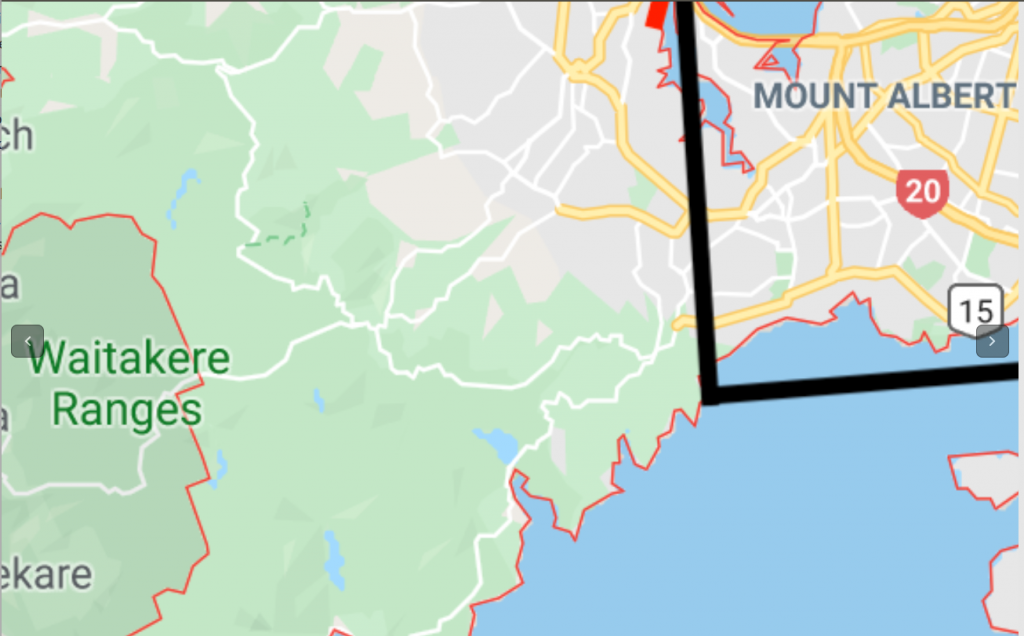
Fig 2. Zoomed in version of Fig 1

We will also use GeoNames, a geographical database that provides useful information about a location such as asciiName, latitude, longitude. This data will be used for a k nearest neighbour search as a backup in case there are no results matching any of the polygon points above.

Solution overview

Here are the steps for the querying the locations, stopping at the first step with matching results:

1. Look for cities within the bounding box(southeast and northwest lat-long pairs). Used for the case when the map is zoomed out. (See Fig 1)
2. Look for bounding box within cities. Used for the case when the map is zoomed in. (See Fig 2)
3. (Backup) Look for the nearest locations from the bounding box using GeoNames data

The main logic

Pre-process GeoNames data

First, we need to write code to download GeoNames data and process them into a k-dimensional tree using the kdt package.

With the kdt package, creating a k-d tree is as simple as this:

kdt.createKdTree(data, distanceFunction, ['latitude', 'longitude']);

The first parameter is the GeoNames data, the second parameter is the function used to calculate the distance between two points on a sphere, and the last parameter is an array of the latitude and longitude field names

1. Look for cities in the bounding box

The first step in the query process is to search for locations inside the given bounding box. Since the rectangle bounding box will be the polygon in which every city will be tested against, a simple range check is needed.

Referring to Fig 1 above, all the relevant cities will be captured if the entire map is taken as the bounding box.

The pseudocode looks something like this:

For each city in polygon list
    For each point in the city
        Check whether bounding box contains point
        If yes, match city to the pre-defined location list and break out of the loop
Return matched locations

Function to check whether the bounding box contains a point

Next, the function to check whether the bounding box contains a point is the key to handle the 3 edge cases of the longitude-latitude crossing over as mentioned above.

Referring to the longitude-latitude map, we can see that longitude(x-axis) can take values from -180 to 180, and latitude(y-axis) from -90 to 90.

These are the conditions that must be fulfilled for the usual case of longitude increasing over the x-axis, and latitude increasing over the y-axis:

• Latitude: southwest latitude <= point latitude <= northeast latitude
• Longitude: southwest longitude <= point longitude <= northeast longitude

Similarly, these are the conditions for the case of longitude-latitude cross over, which need a little imagination to be able to visualise the process:

• Latitude: -90 <= point latitude <= northeast latitude OR southwest latitude <= point latitude <= 90
• Longitude: -180 <= point longitude <= northeast longitude OR southwest longitude <= point longitude <= 180

Here's the javascript code:

const { boundingBox, point } = request;
const { latitude, longitude } = point;
const { northEast, southWest } = boundingBox;

let isWrapAroundLat = false;
let isWrapAroundLon = false;
let isLonWithinNegativeWrappedRegion = false;
let isLatWithinNegativeWrappedRegion = false;

const isLatWithinUsualRegion = latitude >= southWest.latitude && latitude <= northEast.latitude;
const isLonWithinUsualRegion =
    longitude >= southWest.longitude && longitude <= northEast.longitude;

if (northEast.longitude < southWest.longitude) {
  isWrapAroundLon = true;
  isLonWithinNegativeWrappedRegion =
    (longitude >= southWest.longitude && longitude <= 180) ||
    (longitude >= -180 && longitude <= northEast.longitude);
}
if (northEast.latitude < southWest.latitude) {
  isWrapAroundLat = true;
  isLatWithinNegativeWrappedRegion =
    (latitude >= southWest.latitude && latitude <= 90) ||
    (latitude >= -90 && latitude <= northEast.latitude);
}
if (isWrapAroundLat && isWrapAroundLon) {
  return isLonWithinNegativeWrappedRegion && isLatWithinNegativeWrappedRegion;
}
if (isWrapAroundLat) {
  return isLatWithinNegativeWrappedRegion && isLonWithinUsualRegion;
}
if (isWrapAroundLon) {
  return isLonWithinNegativeWrappedRegion && isLatWithinUsualRegion;
}
return isLatWithinUsualRegion && isLonWithinUsualRegion;

With this, the main work required to fix the issue of no matching results when the latitude-longitude of the bounding box crosses over is completed.

2. Look for bounding box in cities

Here, we are looking for bounding box inside the cities.

Referring to Fig 2, Auckland should still show up in the result list even though only a small part of it is visible.

Here steps for this part:

Interpolate perimeters of the bounding box
For each point in bounding box perimeter
    For each city in the polygon list
        Check whether the point is inside the city
        If yes, match city to the pre-defined location list and break out of the loop
Return matched locations

Fig 3. Blue dots are the bounding box inputs, red dots are the other 2 points of the box inferred from the bounding box input. Black dots are the interpolated perimeter points.

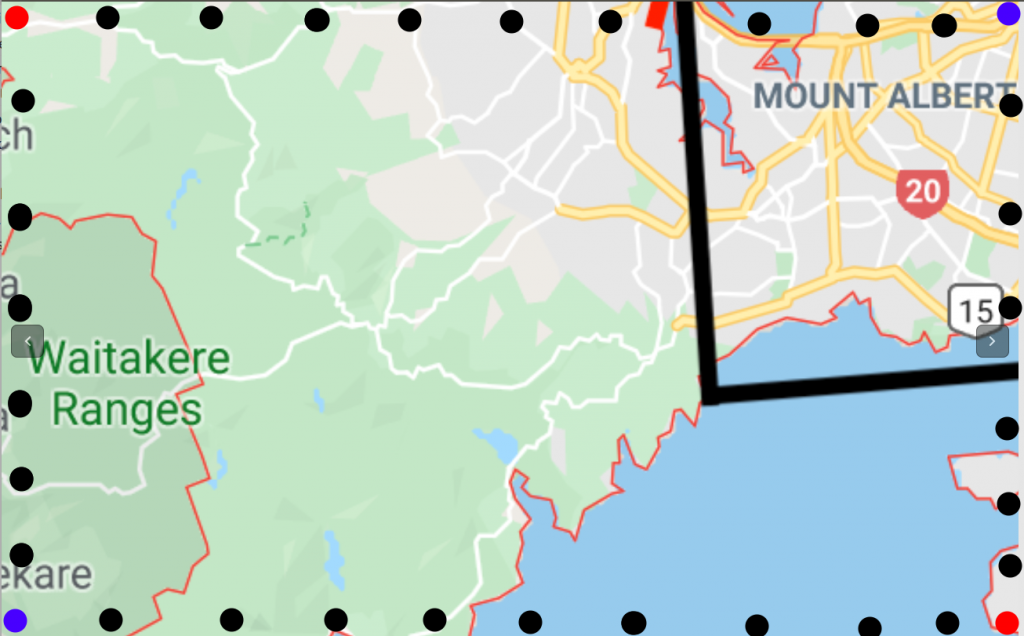
Function to check whether a city contains a point

This is done through the robust-point-in-polygon package.

3. Look for nearest locations from the bounding box using GeoNames data

This third step is used as a fallback in the unlikely event that the previous two steps did not return any result.

Following the pre-processing step of the GeoNames data where the k-d tree was created, it is time to get the nearest neighbours of each corner of the bounding box:

kdTree.nearest(point, 10);

The code above retrieves the 10 nearest locations from one of the bounding box corners. After that, like before, match it to the pre-defined list of locations and return the matching results.

Conclusion

With a working data set of 10 polygons with an average of 12 points per polygon, there is no adverse impact on performance.

If the map is zoomed in, most/all of the results will be retrieved from step 1(find cities in bounding box).

If the map is zoomed out, most/all of the results will be retrieved from step 2(find bounding in cities).

If the above fails, GeoNames will hopefully come to our rescue.