All About Numbers In Javascript

Introduction

In the previous part, we have learned about the different types of data types in javascript. Part-1

we will deep dive into the Number data type in this part

In Other Programming (statically typed) languages like Java or C have different data types for numbers. there is a special space for every type of number to store in memory in Java or C. If we need to store an integer whose range lies between[-128: 128].which both take up only 1 byte If you need to store a larger integer, you can use ‘int’ or ‘long’ data types which take up 4 and 8 bytes respectively. There is also separate data types that you can use to store numbers with fractional parts — ‘float’ which takes up 4 bytes and ‘double’ with 8 bytes. These are usually referred to as floating-point format and we’ll see later where this name comes from.

But we don’t have such a variety of number types in JavaScript. According to the ECMAScript standard, there is only one type of number and it is the ‘double-precision 64-bit binary format IEEE 754 value’. This type is used to store both integers and fractions and is the equivalent of the double data type in Java and C. Some new developers do not realize that and believe that if they use 1 it is stored in 64 bits as:

while in fact it’s stored as:

Let’s, for example, take this loop written in Java:

for (int i=1; 1/i > 0; i++) {
    System.out.println("Count is: " + i);
}

How long will it run? it will stop after the first iteration. On the second iteration the counter i will be increased to 2, 1/2 will produce 0.5 which will be truncated to 0 since the counter i is an integer, and the condition 1/2 > 0 will evaluate to false. Now what do you think will happen if we write the same loop in JavaScript:

for (var i=1; 1/i > 0; i++) {
    console.log("Count is: " + i);
}

As it turns out this loop will never stop because the result of 1/i is not evaluated as an integer, but as a floating point and that leads to very interesting behavior. Want to learn more? Read on. the way JavaScript works usually mentions another unexpected behavior that is easy to explain once you understand the language. Adding 0.1 to 0.2 produces 0.30000000000000004.It’s interesting that this behavior is often attributed to JavaScript, while it’s pertaining to any language that uses the floating-point format for numbers. This means that if you use ‘float’ or ‘double’ data types in Java or C you’ll see the same result.

It is because computers store integers and float differently. I have written a blog about how computers store data type(Int) internally.Link .

How floating-point Numbers are stored in memory?

The IEEE Standard for Floating-Point Arithmetic (IEEE 754) defines many things related to floating-point arithmetic, but we’re interested only in how numbers are stored, rounded, and added. encoded floating-point numbers are actually a sort of compression algorithm by which I mean we're compressing the infinite set of numbers from 0 to infinity and from 0 to minus. all the numbers that come between every single integer we're compressing all of those numbers into the very finite space of a certain number of binary bits.

Understanding how numbers are stored

the IEEE 754 for specification tries to capture as many of those numbers as possible in this system while keeping things sensible but no matter how many bits you have there are always going to be gaps because we simply don't have an infinite amount of space what do you have in the end with this system is a single number format that allows you to express very big things and very tiny things in the sub integer precision and that's something we kind of take for granted now.

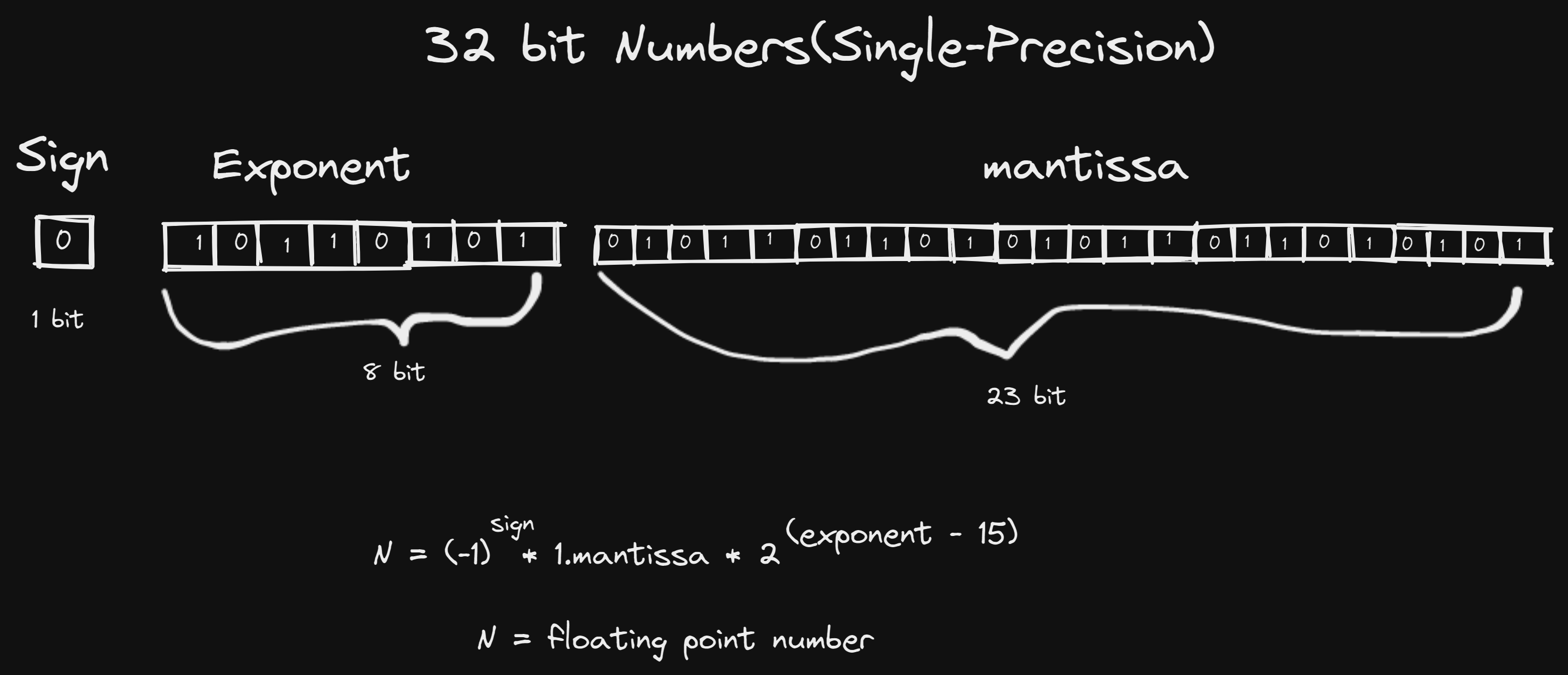
IEEE754 floating point allocates bits to store a number sign, its mantissa (significant digits), and exponent. Here is how it distributes those bits in the Half-precision format (16 bits for each number).

The below image is a representation of 16-bit numbers.

0 indicates a positive value, and 1 indicates a negative.

The below image is a representation of 32-bit numbers.

Let see Why 0.1 + 0.2 == 0.3 is false

Let’s see the bits pattern for 0.1 in floating-point form. The first thing we need to do is to convert 0.1 to binary. This can be done using the algorithm of multiplication by 2. If we convert 0.1 to binary we get an infinite fraction:

The next step is to represent this number in the normalized scientific notation:

learn here scientific notation:

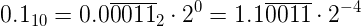
Since mantissa can only have 52 bits, we need to round our infinite number to 52 bits after the radix point.

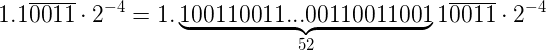
Using the rounding rules defined by IEEE-754 standard we need to round the number up to:

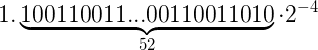
The last thing left is to calculate the exponent representation in offset binary:

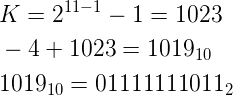
And when put into floating point format representation the number 0.1 has the following bits pattern:

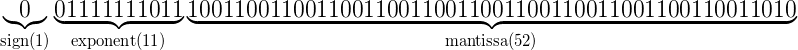
calculate the floating representation of 0.2 on your own. You should end up with the following representations in the scientific notation and binary:

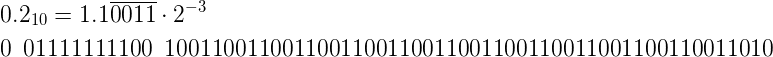
Calculating the result of 0.1 + 0.2:

If we assemble the numbers back from their representation as floating point into scientific form, here is what we have:

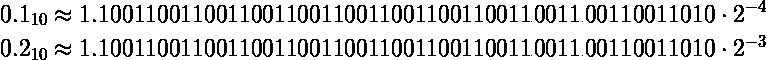
To add numbers, they need to have equal exponents.

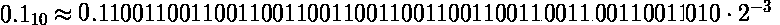
Now we can add the numbers:

Now, the result of the calculation is stored in a floating point format, so we need to normalize the result.

This gives the following resulting number in the normalized scientific form:

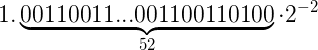
And when converted to the floating-point format for storing, it has the following bits pattern:

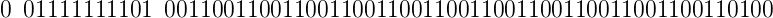
and if we covert this pattern into numbers It will show 0.30000000000000004......, the result of 0.1+0.2 is not 0.30000000000000004 as seen in a browser’s console, but is actually 0.3000000000000000444089209850062616169452667236328125.

So till I covered the basics of how things store internally.

Let's move to Our First Data Type:

Numbers:

In modern JavaScript, there are two types of numbers.

1. Regular numbers in JavaScript are stored in 64-bit format IEEE-754, also known as “double-precision floating-point numbers”. These are numbers that we’re using most of the time, and we have also learned How javascript behaves with Integer and Float numbers.

2. BigInt numbers represent integers of arbitrary length. They are sometimes needed because a regular number can’t safely exceed 253 or be less than -253.

we need to write 1 billion

let billion = 1000000000;

We also can use underscore _ as the separator:

let billion = 1_000_000_000;

Here the underscore plays the role of the “syntactic sugar”, it makes the number more readable. The JavaScript engine simply ignores between digits, so it’s exactly the same one billion as above.

Hexdecimal:

Hexadecimal numbers are widely used in JavaScript to represent colors, encode characters, and for many other things. So naturally, there exists a shorter way to write them: 0x and then the number.

alert( 0xff ); // 255
alert( 0xFF ); // 255 (the same, case doesn't matter)

Different Types of Methods;

1. toString(base):

The method num.toString(base) returns a string representation of num in the numeral system with the given base.

let num = 255;

alert( num.toString(16) );  // ff
alert( num.toString(2) );   // 11111111

2.Rounding:

One of the most used operations when working with numbers is rounding.

There are several built-in functions for rounding:

A)Math.floor():

Rounds down: 3.1 becomes 3, and -1.1 becomes -2.

console.log(Math.floor(3.1)) // 3
console.log(Math.floor(-1.1)) // -2

B)Math.ceil():

Rounds up: 3.1 becomes 4, and -1.1 becomes -1.

console.log(Math.ceil(3.1)) // 4
console.log(Math.ceil(-1.1)) // -1

C)Math.round():

Rounds to the nearest integer: 3.1 becomes 3, 3.6 becomes 4, and the middle case: 3.5 rounds up to 4 too.

console.log(Math.round(3.1)) // 3
console.log(Math.round(3.6)) // 4
console.log(Math.round(3.5)) // 4

D)Math.random():

Returns a random number from 0 to 1 (not including 1).

alert( Math.random() ); // 0.1234567894322
alert( Math.random() ); // 0.5435252343232
alert( Math.random() ); // ... (any random numbers)

E)Math.max(a, b, c...) and Math.min(a, b, c...)

Returns the greatest and smallest from the arbitrary number of arguments.

alert( Math.max(3, 5, -10, 0, 1) ); // 5
alert( Math.min(1, 2) ); // 1

There are lots of methods you can learn in Javascript Documentation

3)parseInt and parseFloat:

Numeric conversion using a plus + or Number() is strict. If a value is not exactly a number, it fails:

alert( +"100px" ); // NaN

in real life we often have values in units, like "100px" or "12pt" in CSS. Also in many countries the currency symbol goes after the amount, so we have "19€" and would like to extract a numeric value out of that.

That’s what parseInt and parseFloat are for.

They “read” a number from a string until they can’t. In case of an error, the gathered number is returned. The function parseInt returns an integer, whilst parseFloat will return a floating-point number:

alert( parseInt('100px') ); // 100
alert( parseFloat('12.5em') ); // 12.5

alert( parseInt('12.3') ); // 12, only the integer part is returned
alert( parseFloat('12.3.4') ); // 12.3, the second point stops the reading

There are situations when parseInt/parseFloat will return NaN

alert( parseInt('a123') ); // NaN, the first symbol stops the process

A bigint is created by appending n to the end of an integer literal or by calling the function BigInt that creates bigints from strings, numbers etc.

const bigint = 1234567890123456789012345678901234567890n;

const sameBigint = BigInt("1234567890123456789012345678901234567890");

const bigintFromNumber = BigInt(10); // same as 10n

Please note though, as numbers and bigint belong to different types, they can be equal ==, but not strictly equal ===:

alert( 1 == 1n ); // true

alert( 1 === 1n ); // false

When inside if or other boolean operations, bigints behave like numbers. For instance, in if, bigint 0n is falsy, other values are truthy:

So Far We have learned a lot. Do ask questions for clarifications and make corrections & suggestions, I expect them. That is all from my end, please share your views in the comment section, and thanks for reading it. Check out my other article Here.Also, Subscribe to my newsletter. Happy Learning