Using the XOR Bitwise Operator

Bitwise Operators

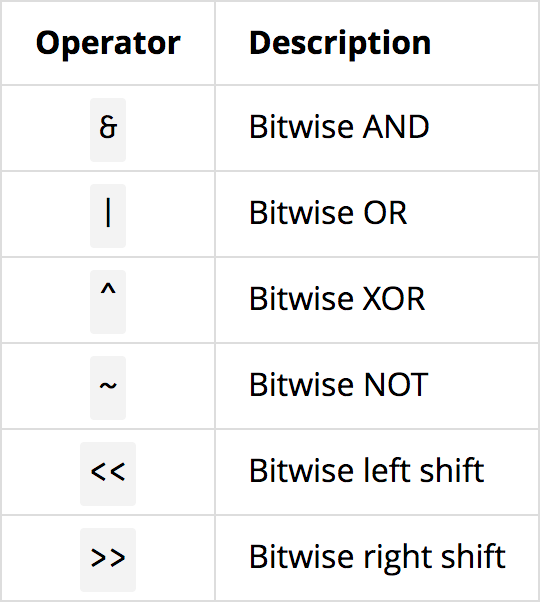
Bitwise operators operate on individual bits in a byte or other binary data. There are six basic bitwise operators:

The Exclusive Or

In this post, I'll discuss some uses for the Exclusive Or (XOR) operator, represented as ^ in most programming languages. Example code will be written in JavaScript, but using the XOR operator will looks very similar in most programming languages.

Like other bitwise operators, the ^ operator performs a logical operation when comparing two bits, or two binary digits of a byte. If the two bits are the same, the output is false/0, and if the two bits are different, the output is true/1. When comparing 1 and 0, we get:

console.log(1 ^ 1);
// => 0

console.log(0 ^ 0);
// => 0

console.log(0 ^ 1);
// => 1

console.log(1 ^ 0);
// => 1

...But when we compare other values, we get interesting outputs:

console.log(5 ^ 3);
// => 6

console.log(4 ^ 3);
// => 7

console.log(5 ^ -3);
// => -8

How It Works

Why are we seeing such different behavior for values that are not 0 and 1? Remember that bitwise operator only compare two bits at a time, one from each of the compared values. The bits compared are digits of the binary representation of the compared numbers, much like a long addition table. Both 0 and 1, in binary, are one-digit numbers, so only one digit from each is compared.

But when we XOR binary values with more digits, like 5 and 3, this is what's going on under the hood:

   101  => (5)
 ^ 011  => (3)
   ---
   110  => (6)

And when we use the XOR to compare identical values, we always get 0:

   101  => (5)
 ^ 101  => (5)
   ---
   000  => (0)

When To Use It

There are many uses for the ^ operator, with notable ones including:

1. Like other bitwise operators, the ^ operator aids with bit-level arithmetic operations that are often much faster than operators using traditional arithmetic operators such as *, /, +, and -.

2. Detecting overflow in the result of an arithmetic operation on a signed binary value. If the leftmost value is 1, it is not the same as the infinite number of 0 digits to the left, and there is an overflow

3. Swapping numeric values with the XOR swap algorithm.

4. XOR linked lists leverage ^ properties to represent doubly linked list structures while saving space in comparison to traditional doubly linked lists.

Single Number

There is another use case that comes up from time to time. Imagine you have a long list of integers, and you know that all but one of those integers is represented twice (or really, an even number of times) within that list. Your task is to find that one "single" number. This is exactly what you are asked to do in the LeetCode problem titled Single Number.

Before learning about the ^ operator, the only solution I could find had quadratic time complexity, or O(n^2). That solution looked something like:

const singleNum = nums => {
    for (let i=0; i<nums.length; i++) {
        let flag = true;
        for (let j=i+1; i<nums.length; j++) {
                if(nums[i] == nums[j]) flag = false;
        }
        if(flag == true) return nums[i];
     }
     return 0;
}

Here I iterate through the input, and for each element in the array I iterate again to check for a duplicate value. This solution works, but it is very inefficient. By leveraging the XOR operator, I was able to greatly improve the time complexity by reducing it to O(n), while saving some lines of code as well:

const singleNum = nums => {
    return nums.reduce((a, b) => a ^ b);
}

We know this solution works, because we demonstrated above that the XOR operator will "cancel out" repeated values:

console.log(2 ^ 4 ^ 2 ^ 3 ^ 4);
// => 3
// because 2 and 4 are cancelled out by their duplicate

console.log(2 ^ 4 ^ 2 ^ 3 ^ 4 ^ 3);
// => 0
// all values were duplicated, so nothing is left over

Conclusion

In this post, we learned:

1. Bitwise operators work on individual binary digits of compared values.

2. There are many uses for the ^, including swapping, detecting arithmetic overflow, and creating memory-efficient doubly linked lists.

3. Because the ^ operator outputs a 0 when compared digits match, and 1 when they don't match, one can leverage XOR to "cancel out" values which are duplicated an even number of times.

One of my favorite aspects of studying data structures and algorithms is discovering novel concepts and applications, which in turn open up new worlds of possibility in designing software. I hope this lesson on the XOR operator inspires you to find new ways to think about the challenges you encounter in your work and studies!