Sudoku Solver (Java Core Approach)

Since in lower primary solving the sudoku has been a major episode for almost all of us especially with the peaks that come with one being announced the winner of the weekly sudoku magazine challenge. This always pushed me to try solve even the complicted puzzled which ofcourse never seemed to be solvable. Coming up with solutions to such mind blowing puzzles is not easy and it requires lots of thinking accompanined by trials and error. As a junior Java developer i will be writing such articles majorly around trying to solve day today problems using Java Core Concepts. Lets begin today's challenge, so usually the sudoku challenge usually entails filling a 9 by 9 matrix with numbers from 1 to 9 and making sure the number only appears once in a given row and column also in a 3 by 3 sub matrix of the main 9 by 9 matrix the numbers are also supposed to appear once. Usually the programming unsaid rules are clear that programming isnt just about writing lines of code but reading a problem and being able to come up with a solution then writing down the logic. Today am going to write the logic of how we can solve the sudoku puzzle, keep in mind that the problem can be solved using so many approaches this is just but one.

NumberNotInRow

This is our first method and the method is going to take 3 parameters: the Row, the Number and the Sudoku matrix. The method will transferse each row of the matrix and search wether th number passed as a parametr exists if it exist the method will return a true if it doesnt then the method will return a false.

private static boolean numberNotInRow(int[][] block, int number, int Row){
        for (int i = 0; i < sudoku_size  ; i++) {
            if(block[Row][i]==number){
                return true;
            }
        }
        return false;
    }

The second method in the project will be called;

NumberNotInColumn

This private class boolean class takes in the sudoku block Array as an argument, the Column and the number. The method will transferse each column of the array and check wether the number passed as parameter already exists if the number exists then the method returns a true to signalize that the number is present if the number isnt in the column then the method returns a false meaning that the specified number can be correctly placed at the entry in the column

private static boolean numberNotInColumn(int[][] block, int number, int Column){
        for (int i = 0; i < sudoku_size  ; i++) {
            if(block[i][Column]==number){
                return true;
            }
        }
        return false;
    }

Since we have worked on determing the entries in rows and columns we now want to create a script that checks whether a number exists within the 3 by 3 small block inside of the big sudoku block. Remember the rule is the number should not be in the Row or Column and also should only appear once in the small 3 by 3 block.

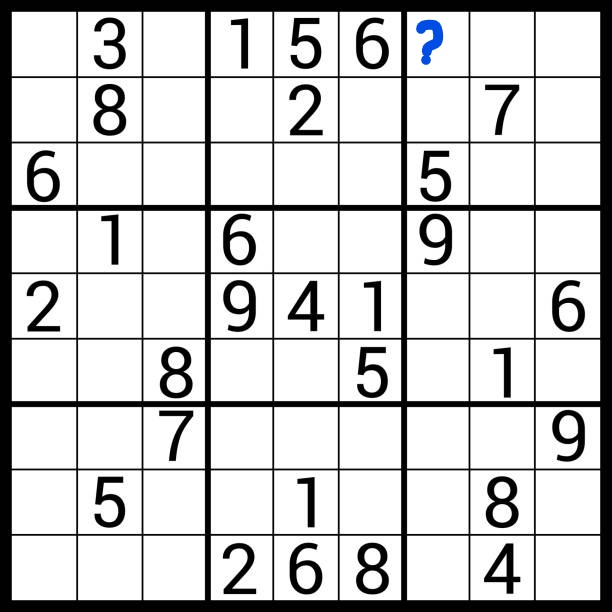
Suppose we want the script to read the entries of the last box in the last box at the top we have to find a way that the loop will start checking entries starting from the question mark horizontally to the end then move to the next row and read horizontally to the end repeat the same untill all the entries in the box are checked. The method will take in the sudoku block, the current Row, the current Column, and the number that is to be placed as a parameter. We first make two local variables to keep track of the position of the row and column in the small 3 by 3 box. Lets give an example for easier understanding. Suppose we want to our loop to begin at the placement of the question mark and loop through the box to check whether the number placement. So lets use an example of the number 7 in the same box, its on Row 1 and Column 7 (Index counting). That means the starting point of the loop will be found by :

• localSmallBoxRow = row-row%3 (1 mod 3 is 1) ie the reminder the division of 1 by 3 localSmallBoxRow = 1-1=0 Similarly;

• localSmallBoxColumn = Column-column%3(7 mod 3 is 1) ie the reminder the division of 7 by 3 localSmallBoxColumn = 7-1 = 6

• So we have successfully found the starting point at Row 0 and Column 6 (index counting starts at 0) where the question mark is placed. We write a for loop to begin from the localSmallBoxRow and stop after 3 entries and move to the next entry by adding one to the localSmallBoxRow entry additionally we add a nested for loop inorder to transfers the columns in the same way the outer loop does. If at a specific entry of the small box the number passed in as a parameter is same as the number presented in the entry then the system returns a true to show that the number exists Otherwise the method returns false to indicate that the number doesnt exist on the placement

private static boolean numberNotInSmallBox(int[][] block, int number, int Row, int Column){
        int localSmallBoxRow = Row - Row % 3;
        int localSmallBoxColumn = Column - Column % 3;
        for (int i = localSmallBoxRow; i < localSmallBoxRow+3; i++) {
            for (int j = localSmallBoxColumn; j < localSmallBoxColumn+3; j++) {
                if (block[i][j]==number){
                    return true;
                }
            }
        }
        return false;
    }

Lets now create one helper class that will help in placement of the number if all the 3 methods we have listed above return false. The method will take in The sudoku block, Row, Column, Number to be checked. and returns only when the 3 methods return false (to show the number is eligible for placement) The helper class is shown below:

private static boolean validNumberPlacement(int[][] block, int Row, int Column, int number){
        return !numberNotInRow(block, number, Row) &&
                !numberNotInColumn(block, number, Column)&&
                !numberNotInSmallBox(block,number,Row,Column);
    }

The next method class will be able to solve the sudoku board. It will have a first for-loop to loop around the Row starting from 0 to the size of the sudoku(9) and adding one after each loop inside the Row loop we nest another for-loop to loop each column starting from 0 to the size of the columns in the sudoku. Now since our sudoku representation was in terms of intergers the blank spaces are represented by 0. So we write an if command to only try and find a suitable number for a specific entry only if the entry is currently 0 (zero) if the the entry is not zero then the script should skip the number. If the if command results to true we write a for-loop that starts from 1 to 9 increamenting by 1 after each loop. Each number produced in the loop will be passed into an if command with our validNumberPlacement method as the argument which inturns takes the number as its argument, the Row, Column and the sudoku block Remember the validNumberPlacement method was a helper method in consolidating all other check methods we listed above that need to be false for the number to be valid. If all the methods are passed it means the number is valid to be placed at a specific block row column entry. Now the solver method has to run recussively so as to replace elements that arent correctly placed and trace back to the previously set numbers.

private static boolean solvingBoard (int[][] block){

        for (int row = 0; row < sudoku_size ; row++) {
            for (int column = 0; column < sudoku_size ; column++) {
                if (block[row][column]==0){
                    for (int NumberToBeTried = 1; NumberToBeTried <= sudoku_size ; NumberToBeTried++) {
                       if (validNumberPlacement(block,row,column,NumberToBeTried)){
                           block[row][column] = NumberToBeTried;
                           if (solvingBoard(block)){
                               return true;
                           }else {
                               block[row][column] = 0;
                           }
                       }
                    }
                    return false;
                }
            }
        }
        return true;
    }

Lastly we write the main method class from which we will call the solver class and also pass the unsolved sudoku. Once solved we write a for loop to output the solved sudoku

    private static final int sudoku_size = 9;

    public static void main(String[] args) {

        int[][] sudoku = {
                {7,0,2,0,5,0,6,0,0},
                {0,0,0,0,0,3,0,0,0},
                {1,0,0,0,0,9,5,0,0},
                {8,0,0,0,0,0,0,9,0},
                {0,4,3,0,0,0,7,5,0},
                {0,9,0,0,0,0,0,0,8},
                {0,0,9,7,0,0,0,0,5},
                {0,0,0,2,0,0,0,0,0},
                {0,0,7,0,4,0,2,0,3}
        };

        if(solvingBoard(sudoku)){
            System.out.println("Sudoku solved successfully");
        } else {
            System.out.println("Board is unsolvable");
        }

        SolvedSudoku(sudoku);
    }

    private static void SolvedSudoku(int[][] sudoku) {
        for (int row = 0; row < sudoku_size ; row++) {
            if(row % 3 ==0 && row !=0){
                System.out.println("-----------");
            }
            for (int column = 0; column < sudoku_size ; column++) {
                if (column % 3 ==0 && column !=0){
                    System.out.print("|");
                }
                System.out.print(sudoku[row][column]);
            }
            System.out.println();
        }
    }

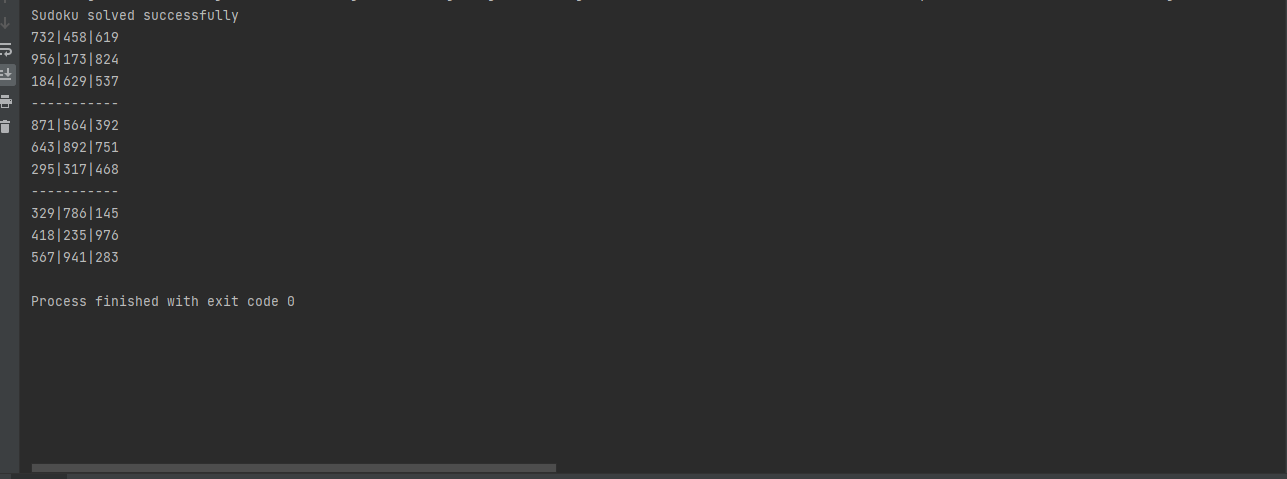
Now one can also edit and let the user enter the values of the unsolved sudoku manually then let the script solve it . Below is the output of the script