What is Mean in Math – Types, Formula with Solved Examples

In Mathematics, we run over insights to gauge focal propensity and scattering. The standard proportions of focal propensities are mean, median, and mode. The scattering comprises of difference and standard deviation. In this part, we will talk about focal propensity and realize what it implies in math. Mean, or math means is the normal of the given arrangement of information or perceptions. Mean is estimated when a transitional worth is required. This worth lies between the outrageous upsides of the introduced assortment of information. We can work out it by separating the number of perceptions by the all-out number of perceptions. What is mean in math? This is a typical inquiry posed by numerous researchers. Mean is the most famous technique for estimating focal inclination. It is utilized primarily for persistent information however can likewise work for discrete information.

Mean = (amount of perceptions)/(complete number of perceptions).

The other two strategies are median and mode. The Median is the center number in an arranged, rising, or sliding set. Then again, the mode is the most successive score in our informational index.

Mean Formula The mean Formula is as easy to comprehend as the mean definition. The mean (or normal) of a few perceptions is the amount of the upsides of the multitude of perceptions separated by the complete number of perceptions.

The image x indicates it, read as 'x̄'

Mean Formula = Sum of Given Data/Total number of information

Computation of mean On the off chance that we have n number of values in information i.e., x 1,x2,x3,… ..,,xn. The mean is given as

x̄ = (x 1+x2+x3+… ..+xn)/n

Likewise, x̄ = ∑ x/n

Number juggling mean The number juggling means is the least complex and most broadly utilized strategy to work out the mean. Coming up next are a portion of the pivotal uses of math mean: In logarithmic treatment. To compute the typical score in sports. In financial matters In human studies Ever. To gauge the world's typical temperature to quantify a dangerous atmospheric deviation. To quantify the yearly precipitation of a specific region. Various kinds of mean The mean or normal most generally utilized is the math mean. In any case, there are a few different kinds of the mean. The utilization relies on the information accessible and the kind of results required.

Following are the sorts of mean: Weighted mean: The weighted math mean is like the number juggling mean. The main contrast is that every information point contributes similarly to the last normal. A few information focuses offer more than others. Weighted mean = Σw.x/Σw

where, Σ = summation, w = the loads, x = the worth.

Instructions to utilize the formula:

Track down the result of the numbers in your information, right off the bat, set, and load. Add every one of the items in Step 1. Put this number away. Presently include the loads as a whole. Partition is the Summation of items by the Summation of loads. a. Geometric mean: Indicates the focal propensity of a bunch of information by utilizing the result of their qualities as opposed to their total.

Mathematical mean = √x 1.x2… .xn where, n = the absolute number of perceptions.

B. Harmonic mean: The mean is determined by the proportional of values rather than the actual qualities. If x 1,x2,x3,… .., xn are the singular things up to n terms, then, Symphonious Mean, HM = n/[(1/x 1)+(1/x2)+(1/x3)+… +(1/xn)]

Symphonious Mean Uses The fundamental purposes of symphonious means are as per the following: It assists with viewing as multiplicative or divisor connections between parts It is many times utilized in averaging things like rates. Benefits and Demerits of Harmonic Mean Coming up next are the benefits of the symphonious mean:

• Inflexibly bound. • Every one of the things is associated with the estimation, for example, nothing is overlooked. • It can propel the logarithmic technique. • It delivers more exact and solid outcomes when contrasted with different means. • It gives the most elevated load to the littlest thing of a series. • It can likewise be estimated when a series holds any bad worth. • It creates a slanted circulation of a typical one. • It makes a bend straighter than that of the A.M and G.M. •
The bad marks of the consonant series are as per the following: The consonant mean is significantly impacted by the upsides of the outrageous things The computation is absurd on the off chance that any of the things is zero The consonant mean computation is tiring, as it includes the examination utilizing the reciprocals of the number. The connection between Arithmetic, Geometric and Harmonic Means The three methods to be specific math mean, mathematical mean, and consonant mean are together known as Pythagorean mean. Following are the recipes: Math Mean = (a1+a2+a3+… .+an)/n Consonant Mean = n/[(1/a1)+(1/a2)+(1/a3)+… +(1/an)] Mathematical Mean = n√a1.a2.a3… an

Allow G to be the mathematical mean, H consonant mean, and A number juggling mean, then the connection between them is given by:

G=√AH

Or on the other hand

G² = A.H

For what reason is Geometric Mean Better than an Arithmetic Mean? The mathematical mean and number-crunching mean are the two strategies to decide the normal. The mathematical mean is in every case, not exactly the number-crunching implies for any two positive inconsistent numbers. Here and there, the 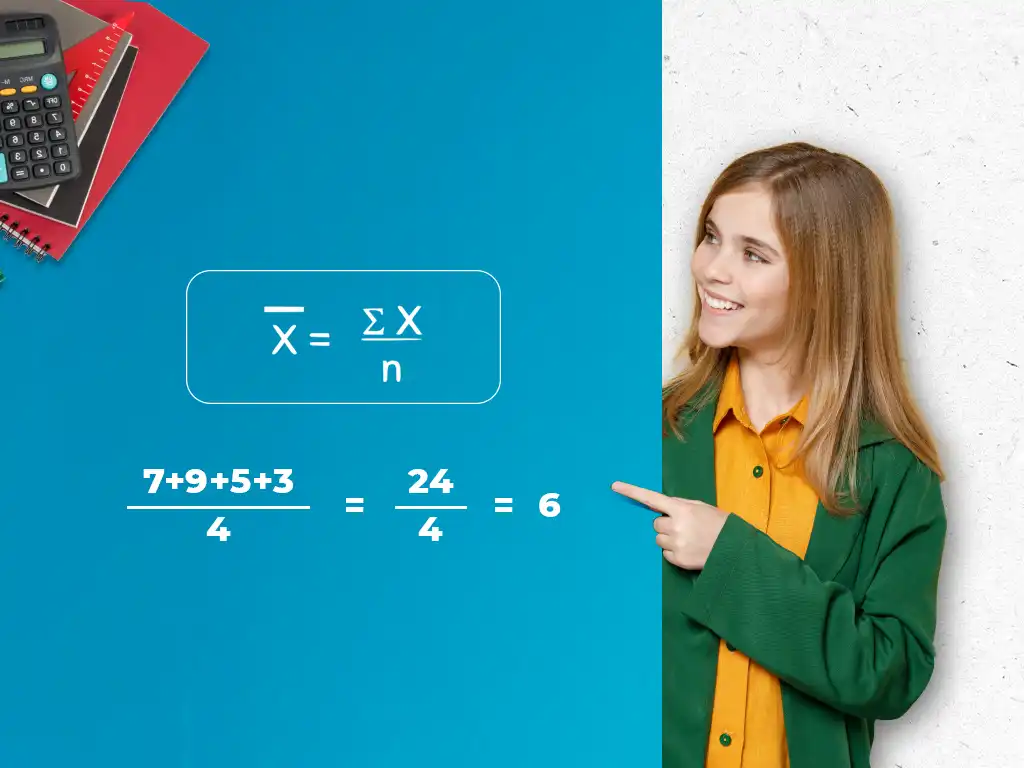umber-crunching mean works better, such as addressing normal temperatures, and so on. To learn more about mean, median, and mode please click here- https://www.turito.com/blog/foundation/what-is-mean-in-math