One may be tempted to believe that Big O is just a notation for the worst case analysis. After all, Big O is an "upper bound" notation. Isn't the upper bound equivalent to the worst case?

For the sake of simplicity, let's assume our algorithms rely on a single variable n. Let's differentiate between two things:

• The upper bound

• The worst case analysis

Big O, an upper bound for functions

When we say a function \(f(n)\) is \(O(g(n))\), we are saying that \(f(n)\) is bounded from above by some constant multiplied by \(g(n)\), for \(n\) sufficiently large. So, the notation essentially states that: the function is bounded from above by some simpler function, by which we can roughly approximate the growth of our original function.

Different Types of analysis can have different growth rates

On the other hand, the type of analysis as being (worst case, best case, or average case), can yield different rates of growth for the algorithm's complexity. So,

• the best case complexity can be \(f_1(n)\)

• the worst case can be \(f_2(n)\),

• and the average case can be \(f_3(n)\).

So, depending on the analysis, we can have different functions, each of which has its own upper bound (Big O), lower bound (Big Omega), or tight bound (Big Theta)!

Example: The Selection sort algorithm

Let's see an example with a simple sorting algorithm: the selection sort of an array.

The best case

The best case for our algorithm is when the array is already sorted. The algorithm will then have a linear number of checks until it reaches the end of it. This means that an upper bound to the performance in the best case can be \(O(n)\)

The worst case

As for the worst case, the array is sorted in reverse order. This will lead to a quadratic number of checks. This means that an upper bound to the performance in the worst case can be \(O(n^2)\)

In a nutshell

• Big O is not synonymous with the worst-case analysis

• Big Omega is not synonymous with the best case analysis

• Big Theta is not synonymous with average case analysis

• Rather, each type of analysis can have its own upper bound (Big O), lower bound (Big Omega), and tight bound (Big Theta).

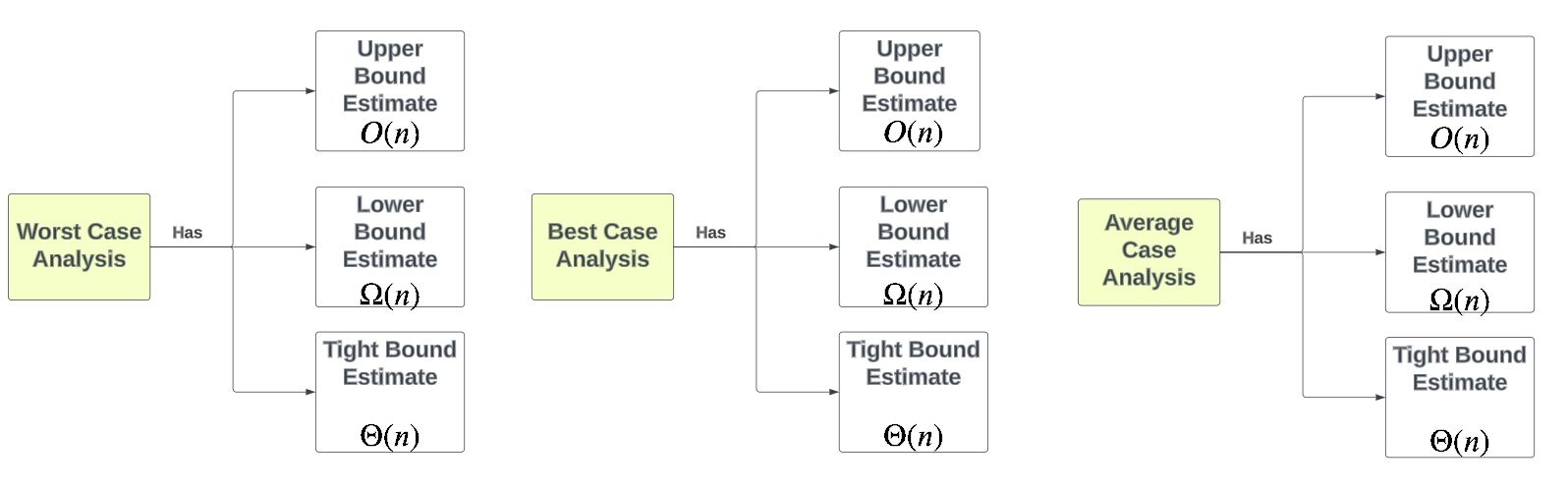
• Sometimes, different types of analysis can have the same bounds. This can be observed in the merge sort for example. Whether the original array is sorted or not, it will take the same number of comparison steps.

Why the prevalence of this confusion?

• Syntactically, the notion of an "upper bound" can be confused with the notion of a "worst case", because they are quite similar if you take them out of context.

• Furthermore, we are usually interested in the upper bounds of algorithmic complexity at the worst case of analysis. So, more often than not, we tend to mention them together, and that can lead some to think they are one and the same.