AlphaTensor : Reinforcment Learning's approach to Multiplication

Just a few days back Deepmind pub it's new paper AlphaTensor, the first artificial intelligence (AI) system for discovering novel, efficient, and provably correct algorithms for fundamental tasks such as matrix multiplication.

In this article we are gonna cover the following topics -

1. Maths Behind SVD
2. TensorGame
3. Challenges posed by TensorGame
   • Synthetic demonstrations
   • Change of basis
   • Data augmentation
   • Neural network architecture
4. Conclusion

Singular Value Decomposition (SVD)

SVD is one of the most important algorithms in linear algebra. You can think of it as a tool that helps in data reduction of Big Data eg. high-resolution images or videos. In the last generation of computational science, we used may be things like the Fourier transform, Bessel's function, and spherical harmonics to map the system of interest to new and simpler co-ordinate. But for example, if we have a complex system like turbulent flow over a Boeing wing, there is no off-the-shelf transformation to cater to this problem but a technique like SVD can be tailored to any general problem This algorithm is literally used all over the place like compression of large data, Google's page rank algorithm, Facebooks's face recognition algorithms and recommendation systems at Netflix, and Amazon to find correlation patterns

Now that I have got you hyped enough let's dive in

Let's assume we have image with a million pixels and it is vectorized to a column vector m x 1 and we use n such images putting them togather to get a m x n matrix where m>>>n (m is in order of millions and n is no.of image in order of thousands) Then that matrix can be represented as

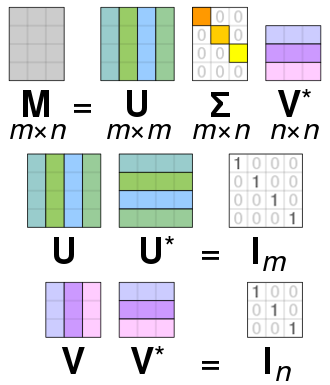
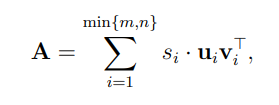
where U , V are orthogonal matrices which is represented in the above image U is of same dimension as of M but with some distortionand that's why you can guess it is called the eigenvector and the sigma matrix is a diagonal matrix till n x n matrix and other than that it's all zero where all enteries are in hierichal order describing the importance of first row of U and first column of V in representing our data M

But we can approximate our data M by just using first k columns in our matrices U , V , W

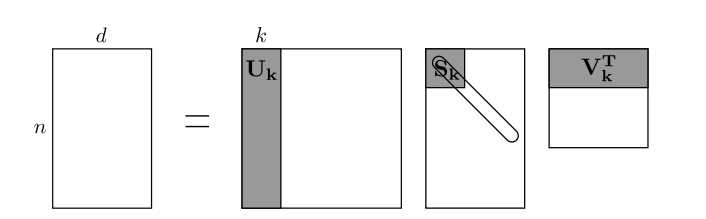
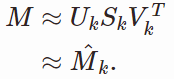
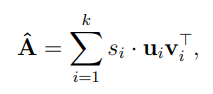
To get a even deeper understanding of SVD I would highly recommend this youtube playlist by Steve Brunton

AlphaTensor

When we talk about efficient algorithms the efficiency doesn’t come from thin air it comes by optimizing our algorithm to the kind of hardware we have . The GPUs or TPUs we use take a lot time in multiplication than addition so if we could reduce the number of multiplication operation by some kind of manipulation and replace it with addition . You all must remember this from your high school mathematics

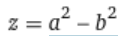
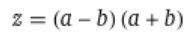
As you can see with a simple manipulation we reduce the number of multiplications from 2 to 1 thus optimizing our calculation and when we do some similar things in a 2 x 2 matrix multiplication we can optimize matrix multiplication

As you can clearly see there can be many combination that we can form with trial and error to get our required result and this is where reinforcement learning come where our agents learns the suitable parameters in form of a game Now we are gonna look at the structure of this game

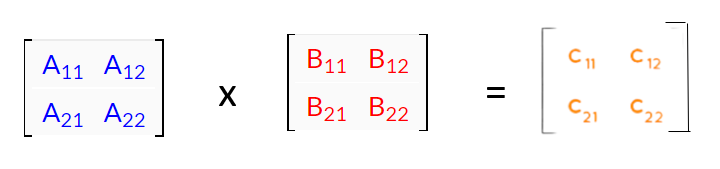
Let’s assume we have two 2 x 2 matrices to multiply (A & B) to get a resultant matrix C

Tensor T2 representing the multiplication of two 2 × 2 matrices. Tensor entries equal to 1 are depicted in purple, and 0 entries are semi-transparent. The tensor specifies which entries from the input matrices to read, and where to write the result. For example, as c1 = a1b1 + a2b3, tensor entries located at (a1, b1, c1) and (a2, b3, c1) are set to 1

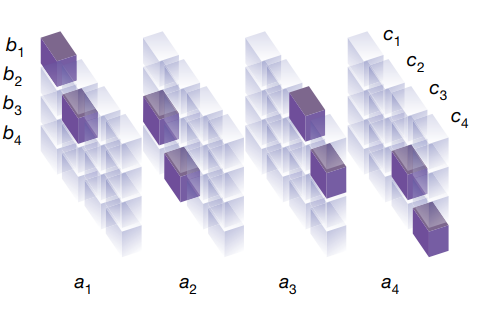
Then if we could do a matrix decomposition of T2 we can find the values of parameter let me unroll this Looking at the given state our agent makes a policy i.e choses a set of triplet (u(t) , v(t) , w(t) ) Let’s assume agent chooses the given combination of u , v , w taking a outer product would give us

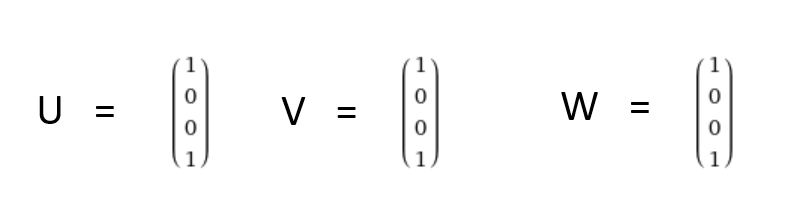
Taking outer product of these vectors would give us ,

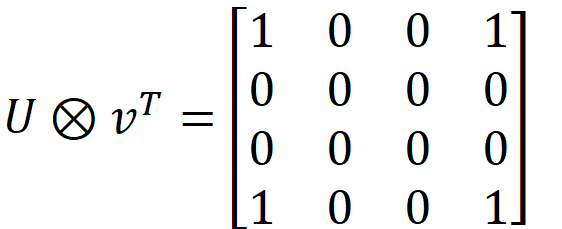
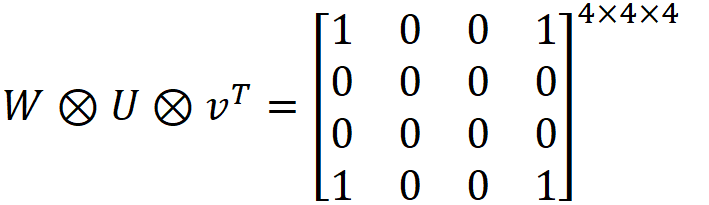
where above picture represents a 4x4x4 tensor with the same 4x4 matrix repeated 4 times in z direction is the rank 1 approximation of the data M

Now if we keep coming up with good values to the triplet u , v, w make 3d tensors with them then add them we shall get back our initial T2

TensorGame

The state of TensorGame after step t is described by a tensor St and initially S0 = T2 then agent finds a worthy triplet find out it’s outer product then subtract the result with the current state , again use that new state and new triplets to find next state and so on . And the game is finally won if after 7 approximation of u , v , w triplet we get the final state as zero which is what it should be if you remember the maths from previous section

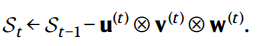
• For every step taken, we provide a reward of −1 to encourage finding the shortest path to the zero tensor.
• , we constraint {u(t), v(t), w(t)} to have entries in a user-specified discrete set of coefficients F (for example, F = {−2, −1, 0, 1, 2}).
• TensorGame is played by the agent AlphaZero1, which achieved superhuman performance in the classical board games of Go, chess and shogi, Similarly to AlphaZero, AlphaTensor uses a deep neural network to guide a Monte Carlo tree search (MCTS) planning procedure. The network takes as input a state (that is, a tensor St to decompose), and outputs a policy and a value.

challenges posed by TensorGame

The main challenge posted by TensorGame is that of a enormous action space . We can overall improve the performance over aplain AlphaZero agent by following methods

1. Synthetic demonstrations

Although decomposition of matrices is a difficult task but the task of making matrices from randomly choosen {u(t), v(t), w(t)} and adding them up to get a matrix is quite easy

Then we can train the network on this diverse set of examples

2. Change of basis

Tn (Fig. 1a) is the tensor representing the matrix multiplication bilinear operation in the canonical basis. The same bilinear operation can be expressed in other bases, resulting in other tensors. To know more about basis you can see this amazing video by 3Blue1Brown

These different tensors are equivalent they have the same rank, and decompositionsobtained in a custom basis We leverage this observation by sampling a random change of basis at the beginning of every game, applying it to Tn, and letting AlphaTensor play the game in that basis . This crucial step injects diversity into the games played by the agent.

3. Data augmentation

From every played game, we can extract additional tensor-factorizationpairs for training the network.Specifically, as factorizations are order invariant (owing to summation), we build an additional tensor-factorization training pair by swapping a random action with the last action from each finished game.

4. Neural network architecture

The network broadly consists of the following components Input, a torso, followed by a policy head that predicts a distribution over actions, and a value head that predicts a distribution of the returns from the current state

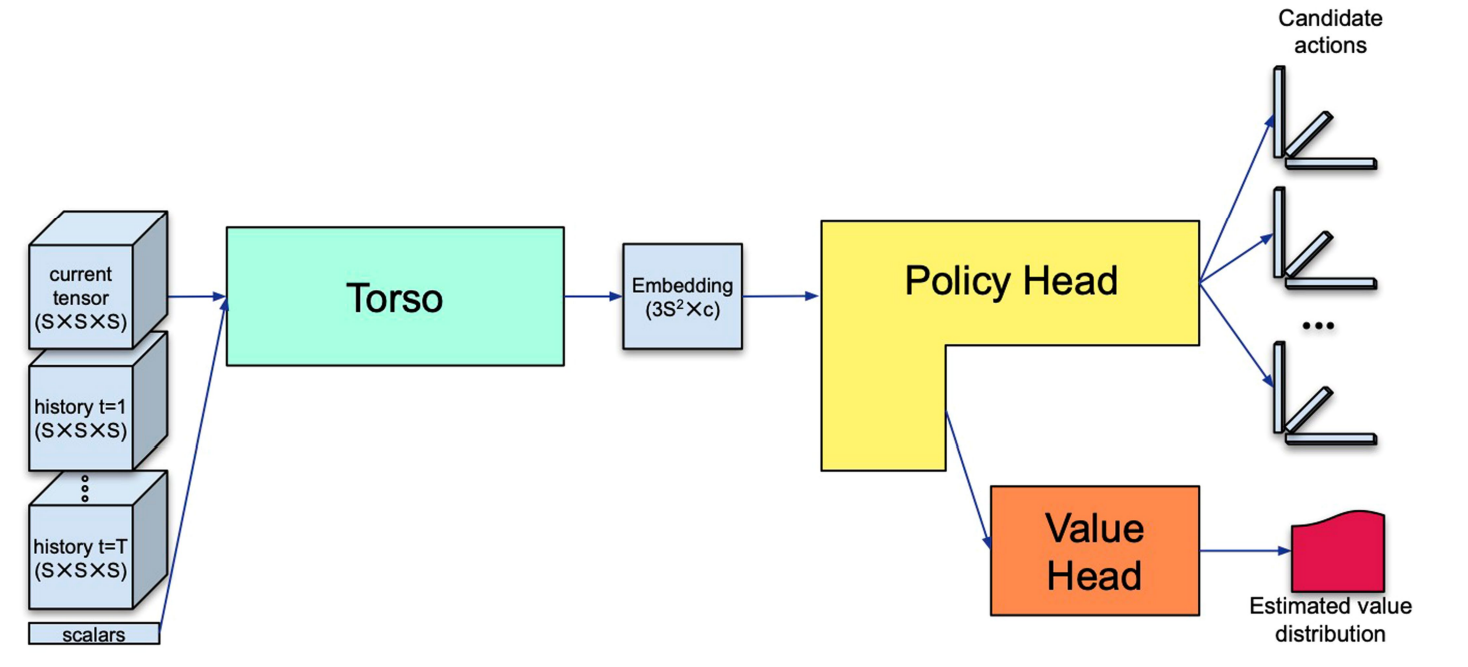
4.1 ) Input - The model is given all relevant information about the current state and the previous state . We plug in the the current state St as a tensor and last h actions (h being a hyperparameter usually set to 7) as a scalar

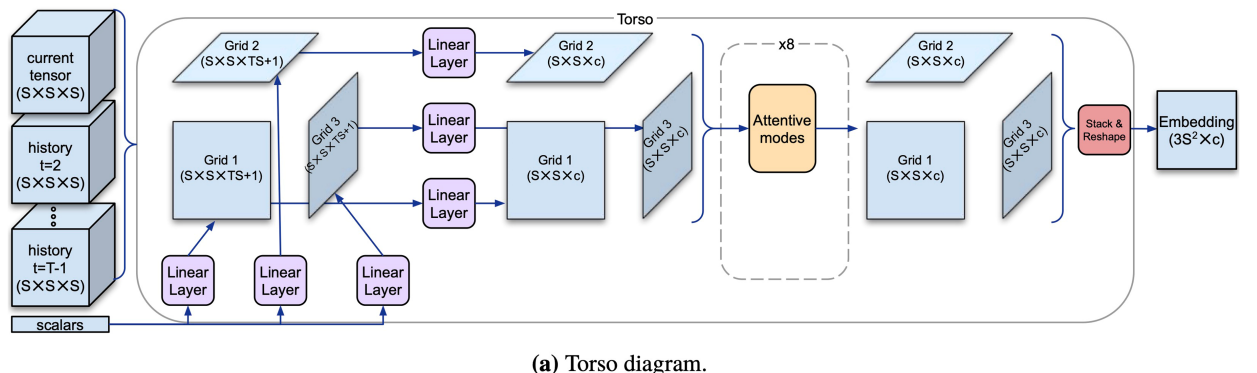
4.2 )Torso - It basically maps the tensors and scalars from the input to a representation that is useful to both policy and value heads It is a architecture based on modification of transformers and its main signature is that it operates over three S × S grids projected from the S × S × S input tensors.

4.3 )Policy Head - Using the embedding generated by the torso network , this architecture gives a possible move for the agent i.e. choosing a correct set of {u(t), v(t), w(t)} given the previous state . The network makes the use of various attention mechanisms form transformers architecture you can learn more about it from this amazing blog

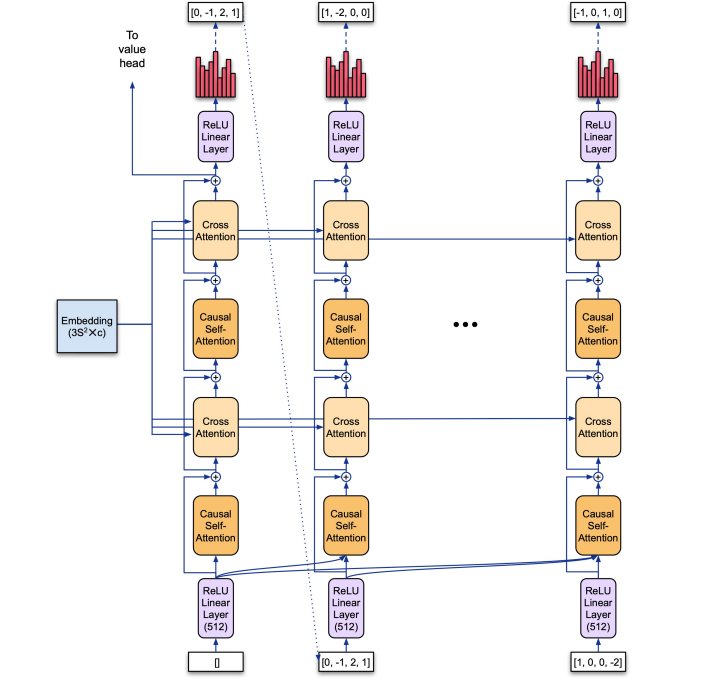
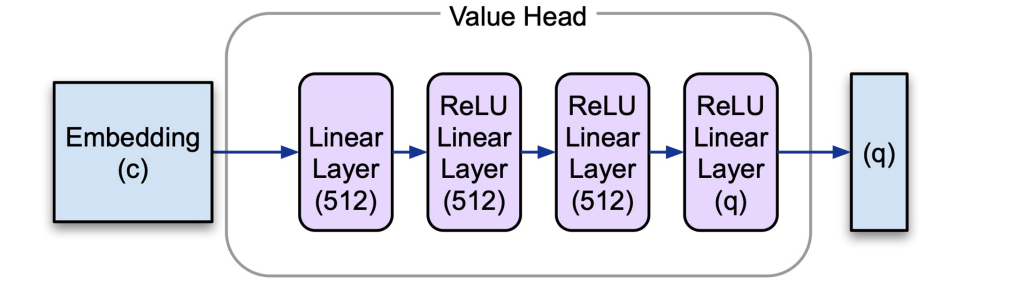
4.4 )Value Head - The value network assigns value/score to the state of the game by calculating an expected cumulative score for the current state s . Actions that result in good state gets higher score . The key objective of our agent is to maximize this score

Conclusion

AlphaTensor’s algorithm improves on Strassen’s two-level algorithm in a finite field for the first time since its discovery 50 years ago.

AlphaTensor also discovers a diverse set of algorithms with state-of-the-art complexity – up to thousands of matrix multiplication algorithms for each size, showing that the space of matrix multiplication algorithms is richer than previously thought . These algorithms multiply large matrices 10-20% faster than the commonly used algorithms.

Because matrix multiplication is a core component in many computational tasks, spanning computer graphics, digital communications, neural network training, and scientific computing, AlphaTensor-discovered algorithms could make computations in these fields significantly more efficient.

---