Minimax in Gomoku

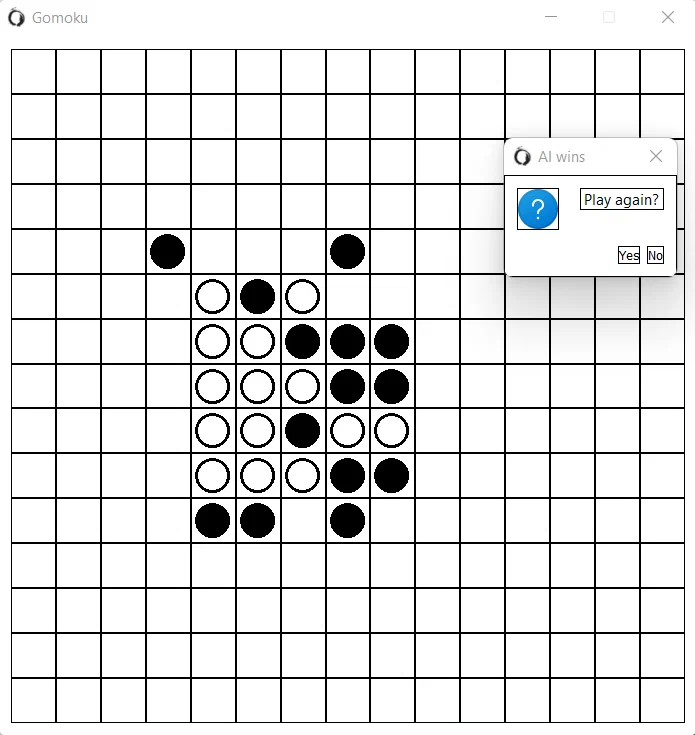
During my bachelor study at MSU we had a very interesting and diverse programming course. In fact it was not a single course, but a series of different courses, where each year we mastered some new algorithms and technologies and then handed our problem set solutions (written mostly in C++) for review and grading. Usually each student randomly recieved either one task or a set of tasks from a large list, bound to some specific topic, and for quite a long period of time (from a few weeks to several months) we were face-to-face with our programming problems. One had to study some textbooks and articles, read student forums, speak with tutors via internet just to find some way to solve the task. Everything could be found useful — sometimes insights for the solution came from forum posts, some information could be recieved from higher-grade students, however most of the time good ideas could be achieved only via communication with teachers. Looking back at that wonderful time I can definately state that this was an extremely useful experience, although sometimes it was quite tough and a lot of stress, especially when some tricky algorithm did not work after another hundred of modifications...

Third-grade programming course was devoted to optimization techniques, where we had to implement some raw solution for a given problem first, measure its efficiency, find bottlenecks and optimize. I was lucky to recieve a task of implementing an AI engine for Gomoku game. Gomoku should be familiar to you, it is a well known «five in a row» game, where on the 15x15 field two players place black and white stones, and the winning condition for any player is to put five stones in one row either horizontally or vertically or on the diagonal line. The task had some formal limits on performance (i.e. it was stated what winning-rate for AI engine is OK), which I do not remember precisely, but what I remember is the fact that my own AI engine was completely out of hand (yes, shame on me). Don't get me wrong, I really tried my best, but could not manage my time right so the solution back then was very simple and I simply did not spend enough time to work on the task as it should be done. It hurts the most that right before my deadlines on this task I found a wonderful article with brilliant ideas on how to make things right, but ran out of time. Still I managed to pass this course and finish my simple engine, but there was a feeling that I have to return to this problem once again in future. So here I am now, found some time to work on Gomoku AI engine once again, but I decided to do everything from the blank, without any references to already existing solutions. Of course my solution that I will be talking about in this article is oversimplified, but hopefully it may be interesting for someone. Here is a quick glimpse on my micro-game GUI:

One important thing that I should mention first of all is that here I will be describing a bad solution, but out there there are good ones. It turned out that in classical Gomoku rules first player (who is playing with black stones) always have a winning strategy (when I was working on this task back in my bachelor study I read that this is only a hypothesis). Thus Gomoku is not so interesting from scientific point of view for me since you can just play in a flawless manner. But I wanted to work with some algorithms though, and this is exactly what I will be describing here. Let us start from minimax method, and the baseline for my description will be this wonderful material from the web.

As a matter of fact, minimax is a method that thinks about game as of a tree with vertices representing states on the board. Every vertex is some specific state and new move from any player changes state to the new one. In Gomoku players make moves consequently, so in such a tree each level will be a move from the different player. One can simply draw such a tree on a paper starting from any possible state of the board. In this tree any vertex will have as many children as there are possible moves from the current state for the opponent. I would like to refer to the image from this article which contains a very good illustration of the tree of states for the simplified version of Gomoku — Tic-Tac-Toe game:

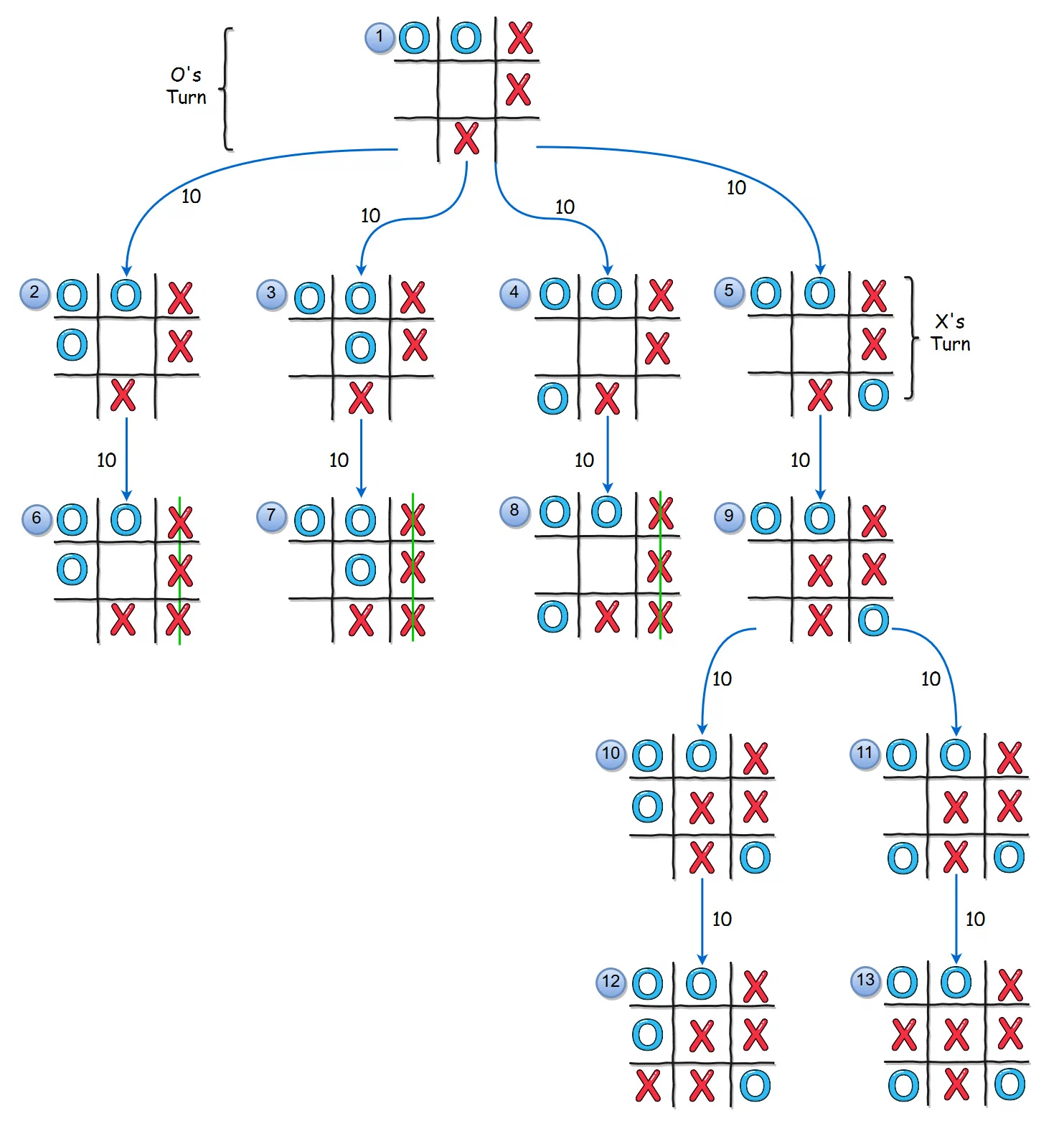
Looking at this picture we can ignore numbers on arrows for now — their meaning will be clear a bit later. The interesting part of this picture is a process of building some possible scenarios of players moves. Also notice that the tree building process stops right there if some of the players made a winning move.

If only we could have a perfect computer with infinite memory that could manage unlimited number of operations per seconds, it would not be difficult for us to write such an AI engine that will always pick a best move and eventually win in case a winning sequence of moves exists. Indeed, such a program would just build a tree until all the layers would be finished and pick a path in that tree that leads to inevitable win. The tricky part here is that such a tree by itself would not store information where is the winning sequence — we have to find it, i.e. we have to store some information for each vertex in the tree if there is a winning sequence below it and where to go starting from this node. Here is where minimax algorithm really starts its work. Let's look at a listing that (I hope) contains enough comments to get the first insight in minimax approach.

There are several things to point out in this code:

1. This is a recursive method, which means it may be very dangerous if we do not understand what will be the recursion limit (if only you are not a stack-overflow error fan). It is quite obvious that in case of Gomoku upper limit for child vertices from each node is 225. This number, surely, becomes less from move to move, however we have an exponential growth here with a tremendous base, and inside each recursion step some computations should be made... Looks like there won't be a good computer to build entire tree in a considerable time.

2. In the listing above some complexity is hidden by beautiful function names. For example there is a function called evaluate which somehow evaluates (oh, wow, really?) state of the board and returns a number that corresponds to some cost of a move. Without additional explanations it may be hard to grip what is evaluate's complexity.

3. Functions getChilrenConfiguration and isLeaf seem to be intuitively clear, however in real life this can be also a very complex computation that should be taken in consideration. One could wonder if the same holds for function type, but here things are not so dramatic, this is easy to compute, i.e. just store for each vertex in a tree what type is it.

4. As we can see some positive infinite value (MAX_VALUE) corresponds to win of player 1 with black stones, and negative infinite value (MIN_VALUE) means the same but for player 2 with white stones. In between these two infinities there are a lot of numbers, and they probably should be somehow used to represent if the board right now tending to some player's win (i.e. if cost is higher, player 1 seems to have more chance to win than player 2). Why we actually need this stuff will become more clear when we'll start coping with problems mentioned in first item of this list.

Ok, I hope that the main idea so far is more or less clear. How then should we work with real computer, since perfect one is far beyond our reach? Well, one of the options is to limit recursion depth of our algorithm. This will lead to loss of information about tree and our algorithm won't be able to predict too much ahead, but it is better than nothing. Here is the sketch of how it should look like.

In the listing above the only thing new is recursion depth — it allows us to finish in finite time with hard tasks. We lose precision of forecasting, but win speed. This is already good, but can we do better? In fact, yes, and this is exactly what alpha-beta pruning does:

The above listing is a bit more tricky, what we added are variables min and max that act as a threshold during our search for best move. If we see that some cost after evaluation exceeds the given threshold this is enough for us to stop computation of that branch of a tree and return the cost value. If this listing is not clear enough than I would recommend you to read the actual note that I already referred to, it is very informative. One should mention, however, that pruning is not always speeding code up, this is extremely dependent on the order of a child nodes (I recommend you to think of an actual example when pruning won't work at all by yourself, you can also find one following the previously mentioned link).

All right, now when we hopefully understand all the basics, let's look at how I made minimax inside my project. Full code can be found here, but we are mostly interested in these lines:

There is actually something that looks like minimax here, but some changes also appear. What are they for?

1. In my code I return not only evaluation of the board, but also recursion depth. I use this patch to choose between several wining sequences the one which is easier to achieve. I'm quite sure that this is a wrong thing to do and everything can be made in a more natural way, but this one was easier for me to do at once.

2. Inside minimax I transmit variable last_moves and flag only_closest which is set to True by default. Usage of flag is quite obvious — during search between children nodes I do not want to evaluate moves that are too far from the already made moves on the board. This is a heuristic approach but it seems to be logical. Variable last_moves is in fact a tuple which stores sequence of moves, that was analyzed during our descent in recursion steps. I simply use this sequence to speed up evaluation (and probably it is also not so brilliant as it could be).

Last question is, how should we evaluate board, what does this magic function actually calculate? Well, that is the most valuable part, good evaluation functions requires good skills (which I don't have, unfortunately). Still I tried to use some imagination (ha-ha) and made some code, which I would like to comment first.

My evaluation function simply «rolls back» the sequence of moves that it receives and the moves themselves are always temporary stored on the board during recursion descent, but then cleared back when going up. Moves are stored in a 2D array self.board and values can be only 0, 1 and -1 (move of player 1, move of player 2 and empty cell). For each new move in last_moves we search for lines of the same color on the board that go through that move, count their lengths, count their «costs» and whether these are «blocked» lines from any of the side. Then we add this new cost value multiplied by some additional weight which depends on flags of blocks from any of the side. In my code positive_directions are simply pairs of integers that represent 4 directions to neighbors out of 8 possible (in positive side of Cartesian plane). And here is the code itself:

As you can see, no rocket science here. I also added in this project an ipynb file and a simple GUI in PyQT5 — both can be used to play with this simple AI, player moves first with black stones. By default recursion depth is set to 3, which seems to be enough for the code to run quickly but still make the game interesting. If you set this to larger value it becomes less comfortable to play, unfortunately (at least on my PC). This is a large problem and of course the actual source of this problem is my inefficient implementation (i.e. I could do that in C++, not in Python). I first wanted to make things better, but then some other interesting topics appeared, so ¯_(ツ)_/¯ ...

Hopefully, some interest to this task will appear in my future work and I will make it better-faster-stronger, probably will make a quite better evaluation function. It may be interesting to play with reinforcement learning on Gomoku, some frameworks even exist, but this is a story for the next time probably.

I hope that this article was interesting for you and you could find something new in it. Don't forget to react and follow me if you want some more of such stuff.

And also do not be ashamed to write any naive and inefficient implementations if you learn some new topics, this actually helps a lot to get a better understanding (anyway your code will be better than mine)!

Thank you for reading and wish you all the best! (And wish you to always find all the winning strategies in life =))