Graph Traversal

Traversing

Let's imagine you have a puzzle🧩 with many pieces having arrows➡ on them that show you, where you can go next. To solve the puzzle, you have to visit every piece keeping in mind not to visit anyone twice. That's what ''Traversing'' the puzzle means.

Graph Traversing

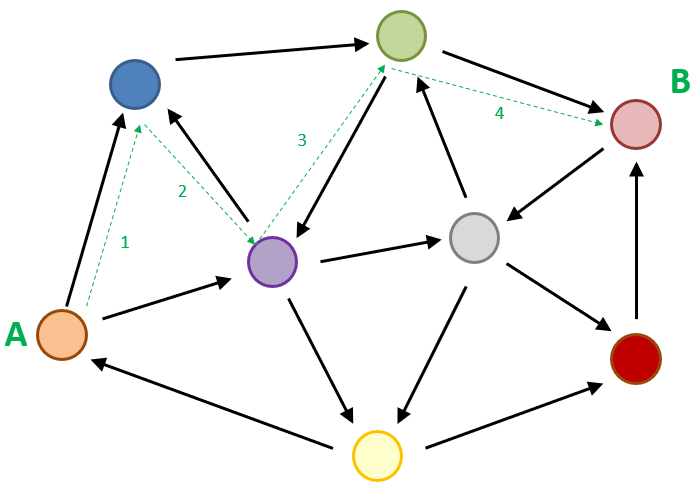
Now consider the big puzzle as a graph, with different pieces as nodes and arrows as the edges. The process of visiting all the nodes in a graph(each node only once) is known as Graph Traversal.

There are two main types of graph traversal in data structures: breadth-first search (BFS)➡ and depth-first search (DFS)⤵️

Breadth-First Search -

Let's start with an example,

Breadth First Search for now just for the sake of explanation consider this as Big Festive Season (BFS)✨, don't give me a look👀 let me explain this.

Consider you are somewhere standing in-between and you have to visit all your loved ones for Christmas🎄, so the basic logic is, you have to go first to the closest house which is in your neighborhood then go ahead on and on.

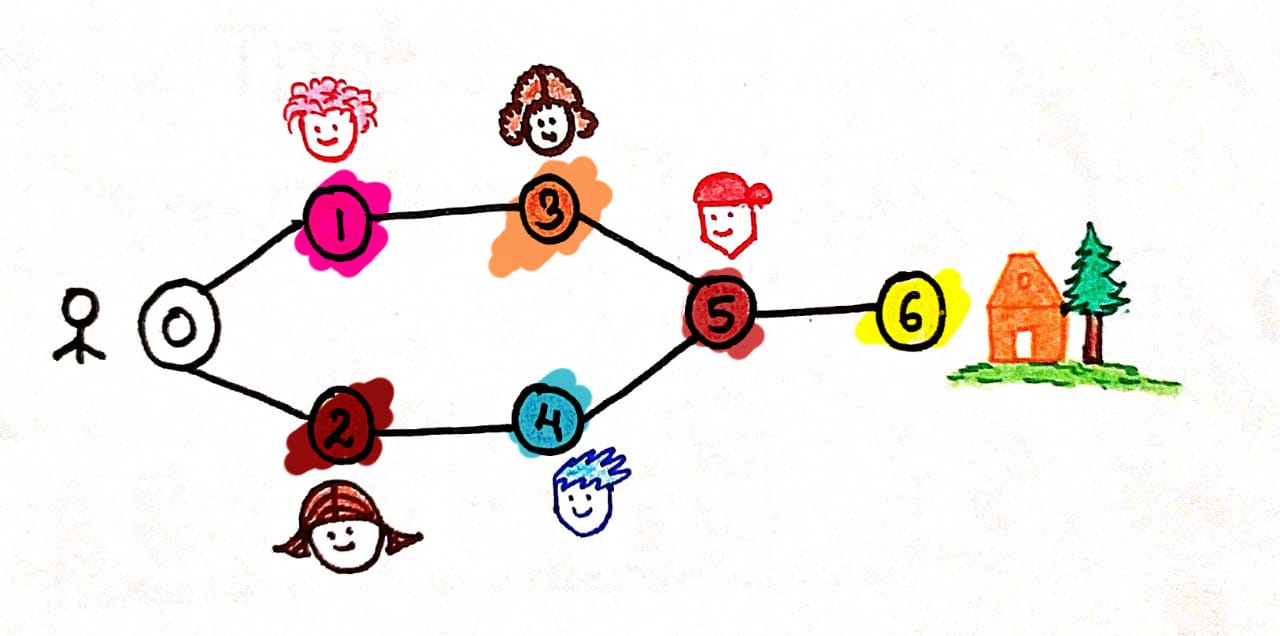
0- You, 1,2,3,4,5- Your loved ones💝 and 6 is Your Home🏡.

If you visit the 4th node first or the 5th node or start from somewhere in-between, Christmas eve will end and you might end up reaching your home soo late or maybe on the next day🥴.

But If you go with the bfs technique by visiting your neighbor first ie, node 1 and node 2 which is the nearest path say,(edge L0) from you, then go to the next street (Level1) node 3, node 4 which is the neighbor of the previous node and then follows the path and so on. So you can reach your home (6) on time by visiting all the houses (nodes).

Also, take note📒 listed with all the names where you have to visit and tick them right✔️ after visiting each one. So that you shall not re-visit any of them even by mistake.

[Breadth First Search => Big Festive Season => Christmas🎅 => Visit Neighbours first]

Checklist✅ = you would keep track of which intersections you have already visited so that you don't accidentally go in a loophole.

*You don't have to remember this, this is just for fun learning😜 So it just clicks on your mind🧠 what you have to do in bfs approach.

Algorithm:

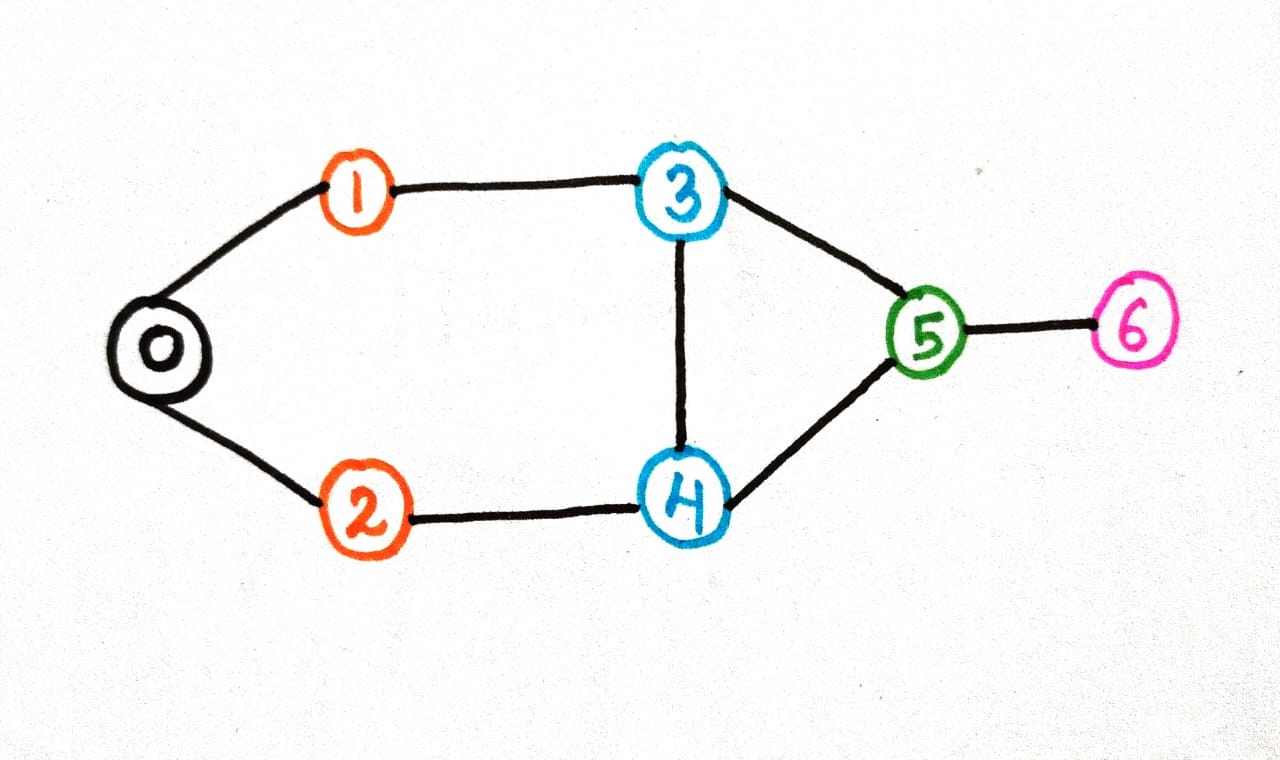
Consider the graph below:-

Step 1- Create a queue and add the root source node (here we'll take node0) to it which is the current node.

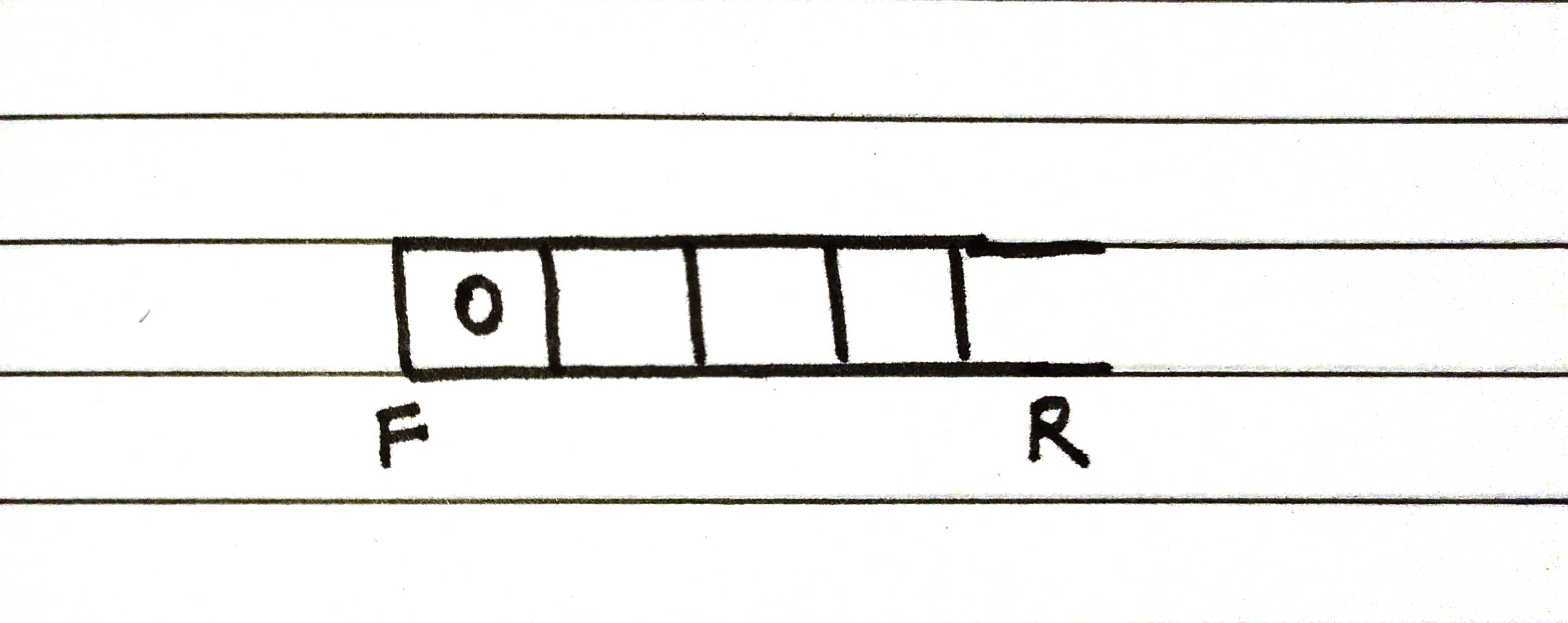
F -> front of the queue, R -> rear of the queue.

Step 2 - Create an array list to track the visited nodes.

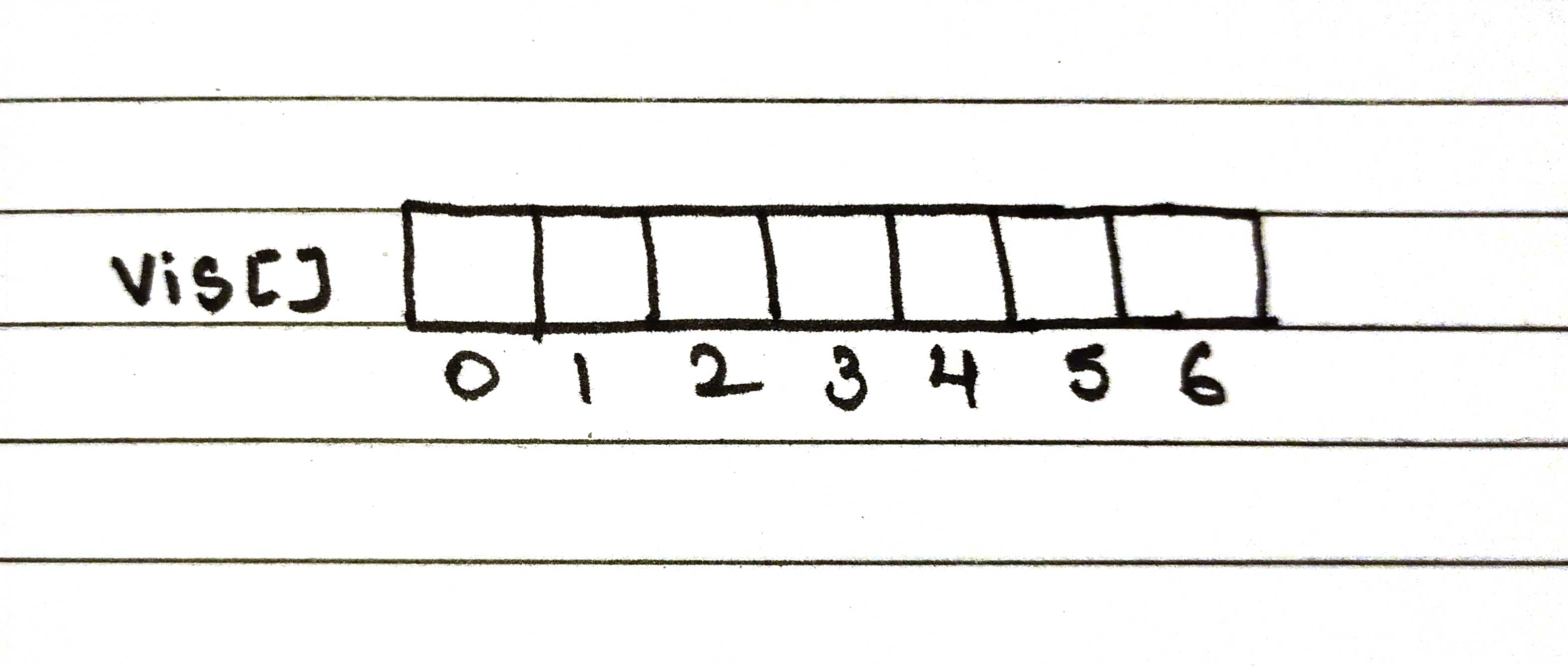
Step 3 - Run the loop till the queue become empty

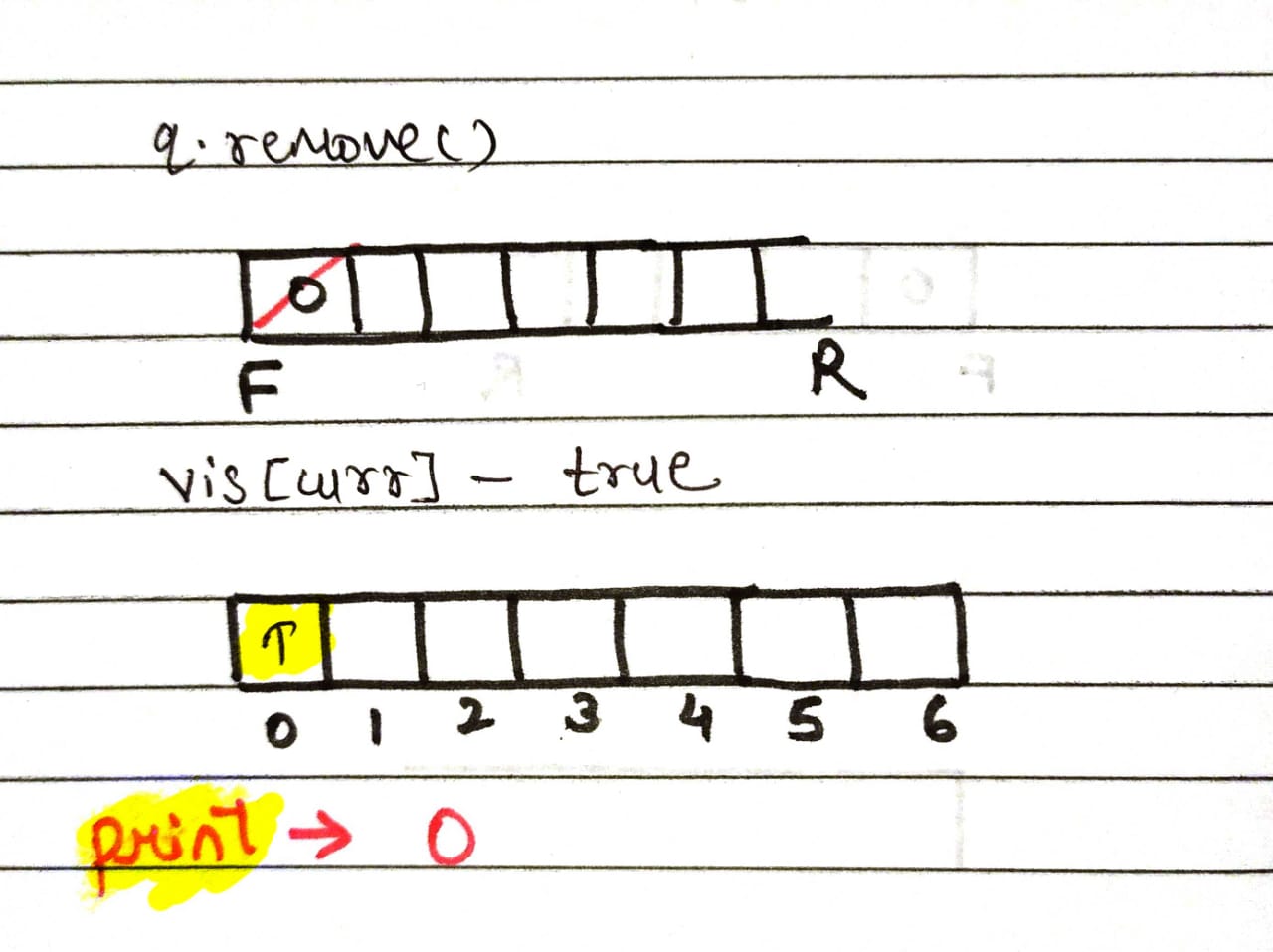
a. Remove the node from the queue and make it the current node

b. If the node is un-visited ie, false (by default) then, mark the current as visited ie,true and print it.

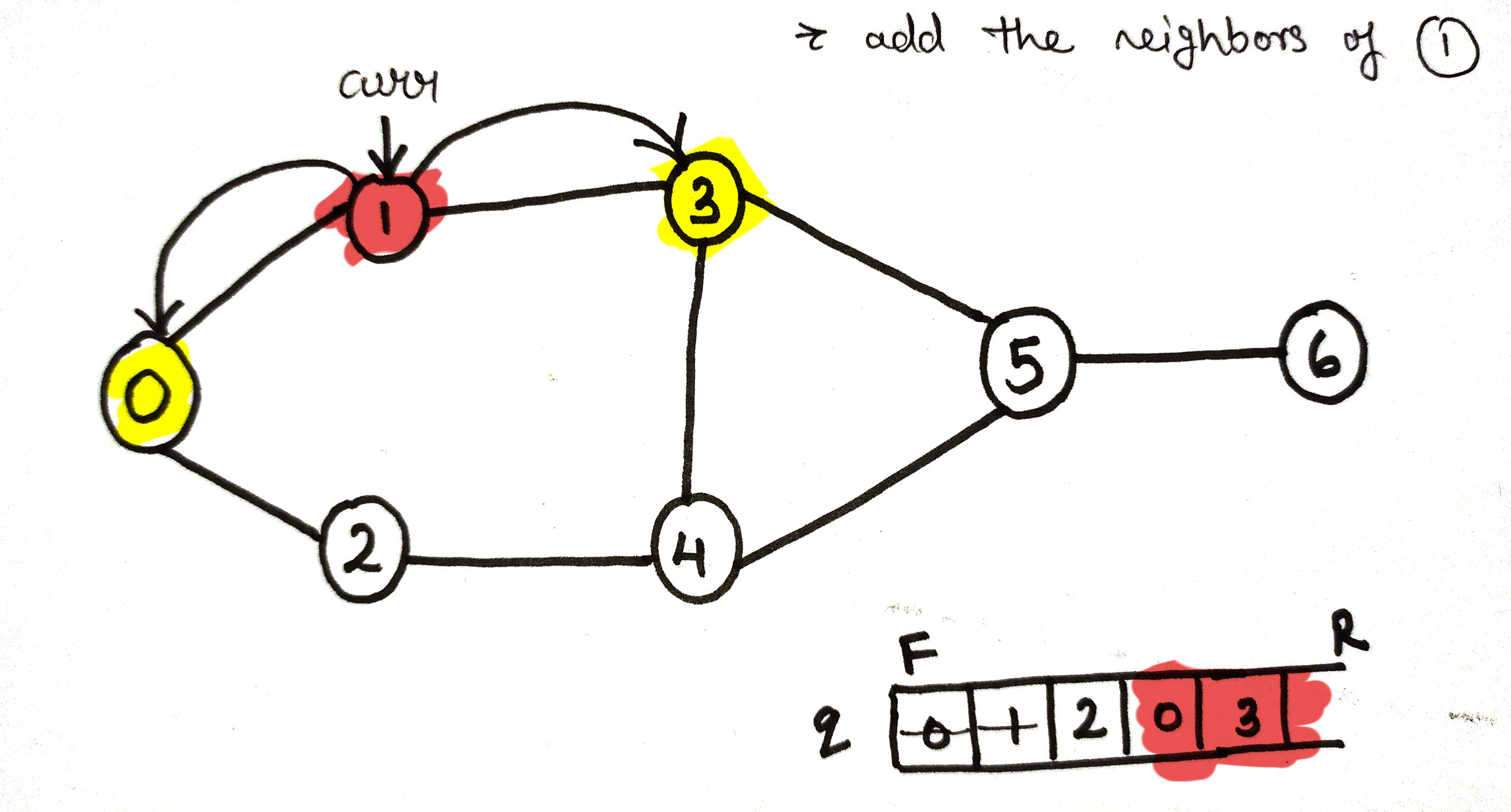
c. Now, add all the neighbors of the current node node 0 to the queue.

Dry Run:

adding all the neighbors of node 0 ie, node 1 and node 2 into the queue⬆.

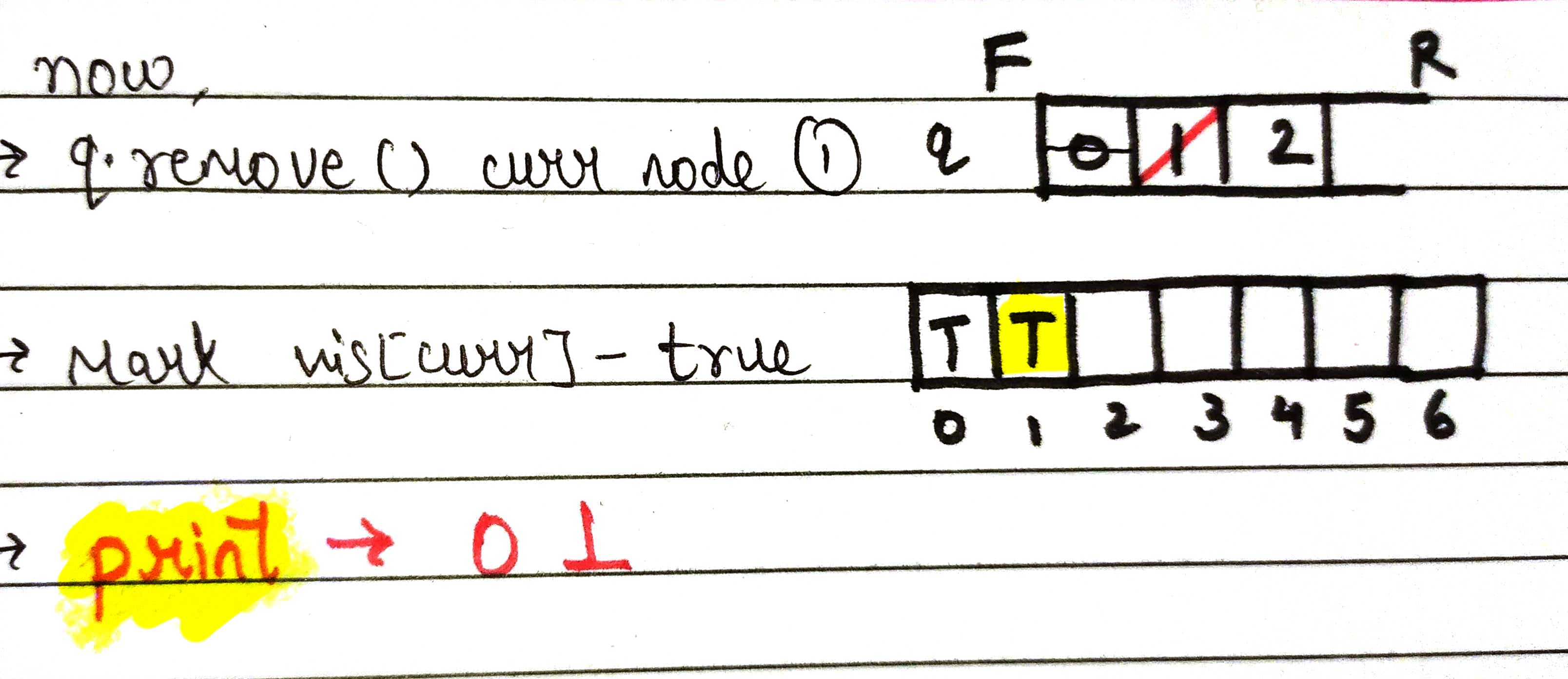
when node 0 is removed, the next node ie node 1 becomes the current node of the queue.

now, here the current node is node 2 ⬇,

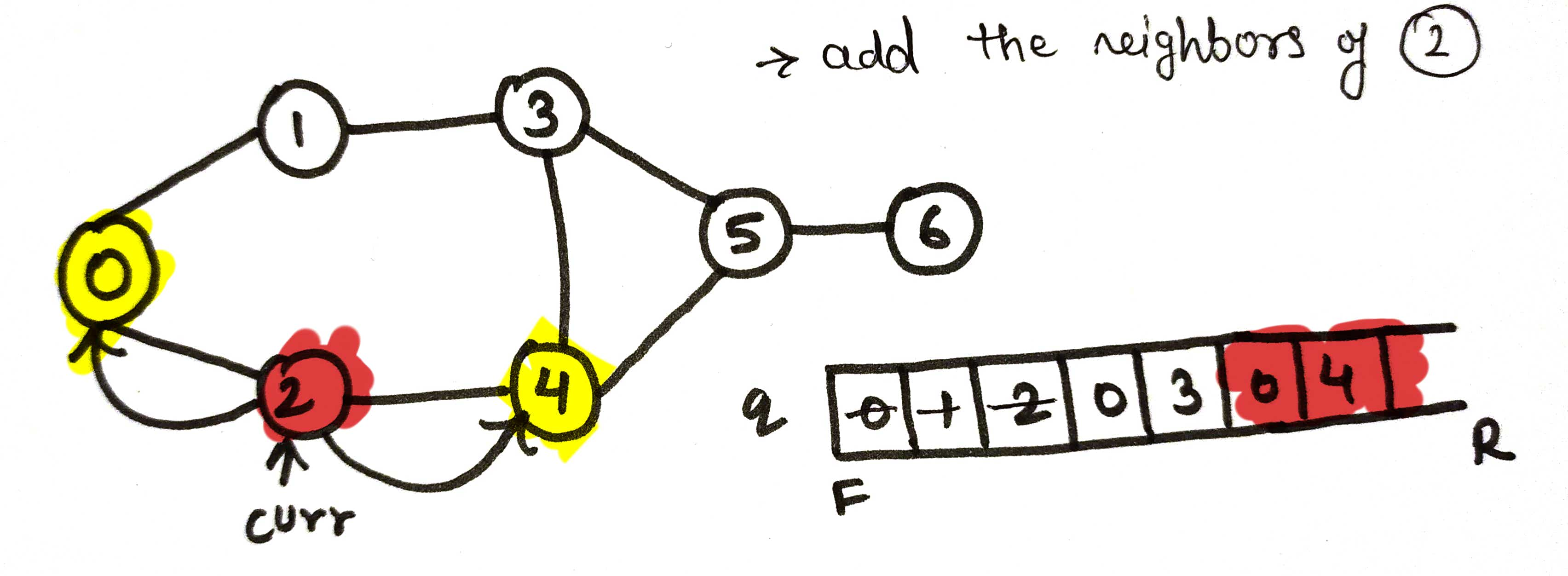
now the current node is node 3 ⬇

here the current node will be node 4

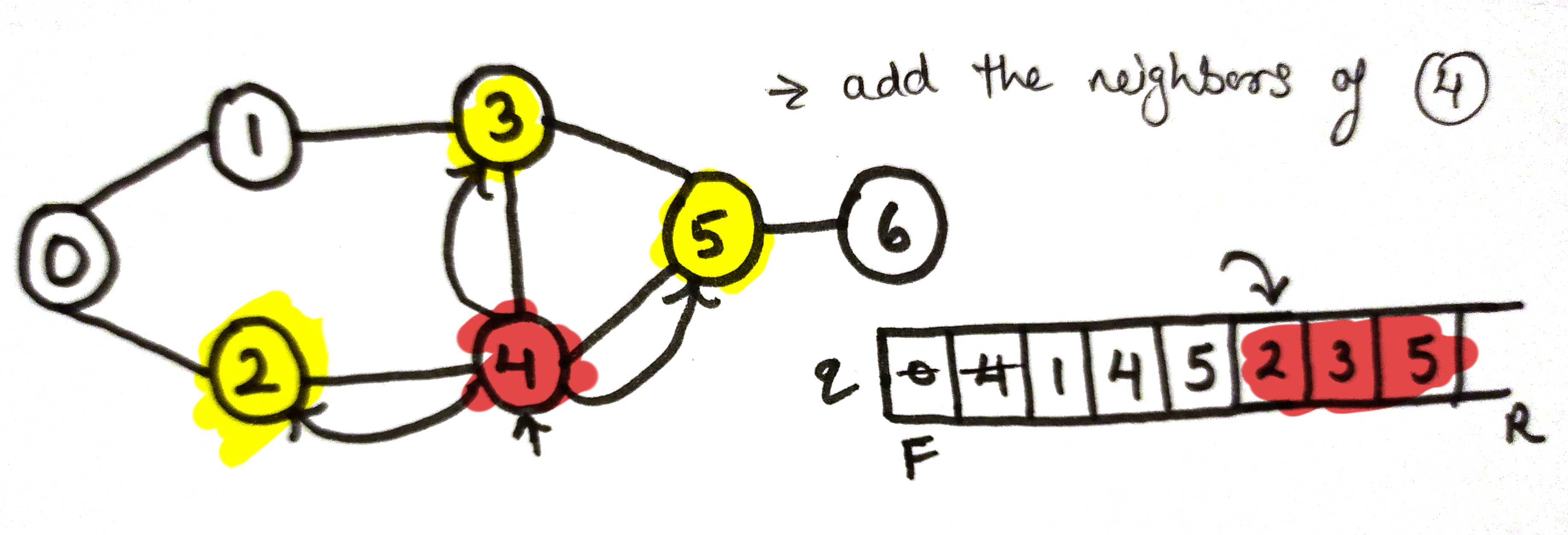
current node = node 5

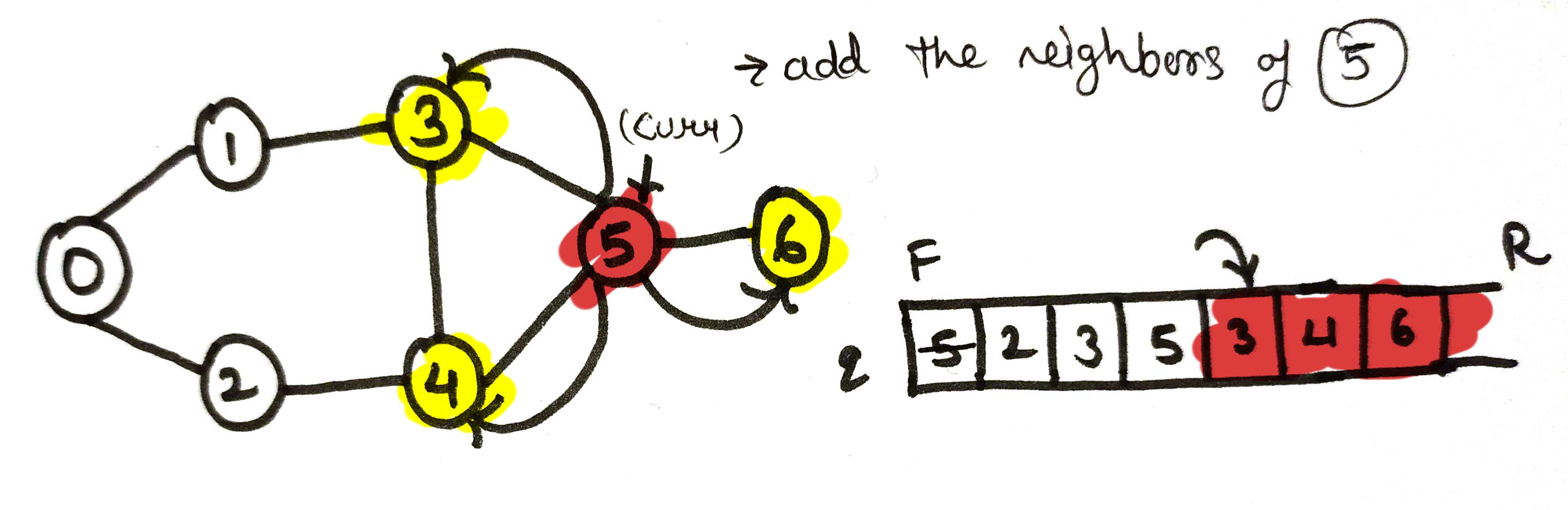
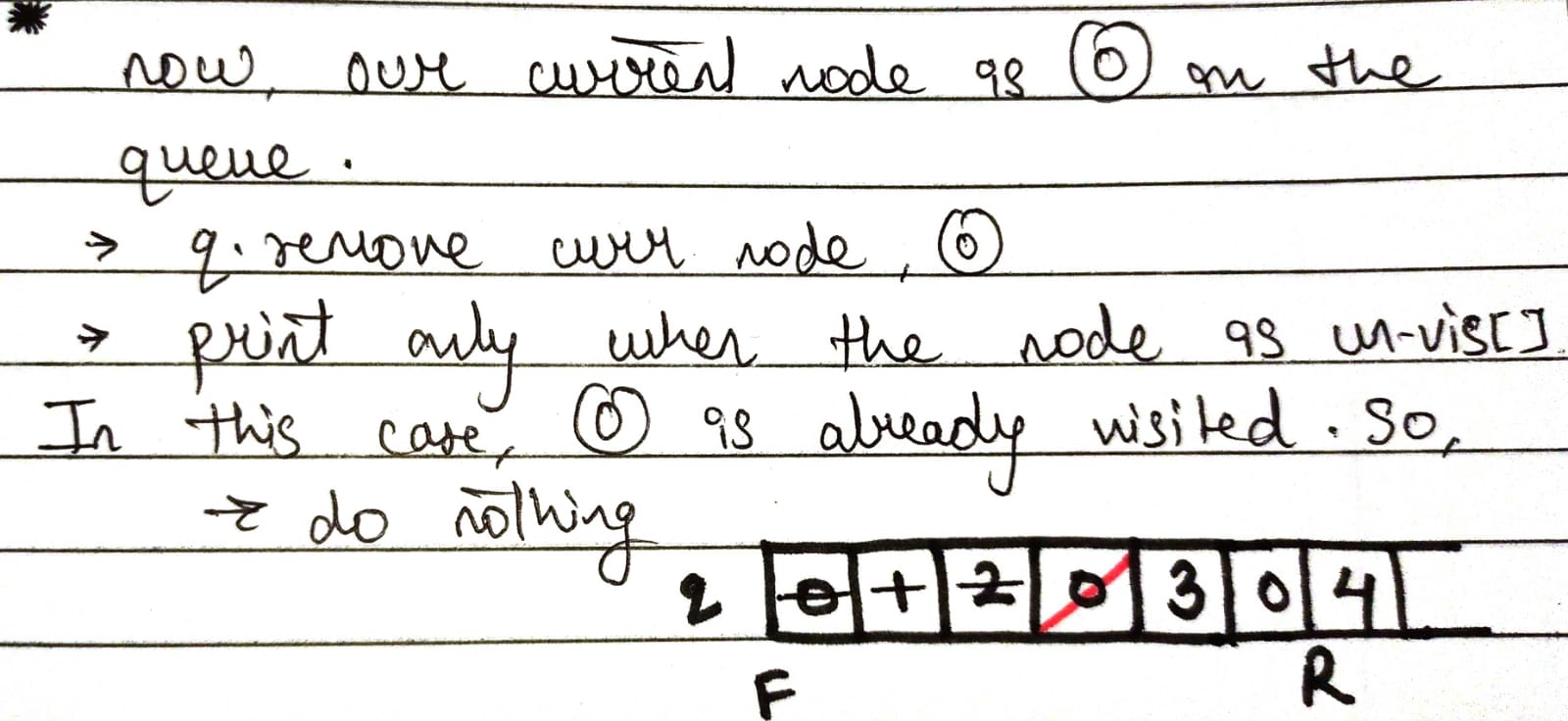
now, q.remove() the curr node ie 2, node 3, node 5, node 3, node 4 and node 6

and do nothing as it is visited nodes.

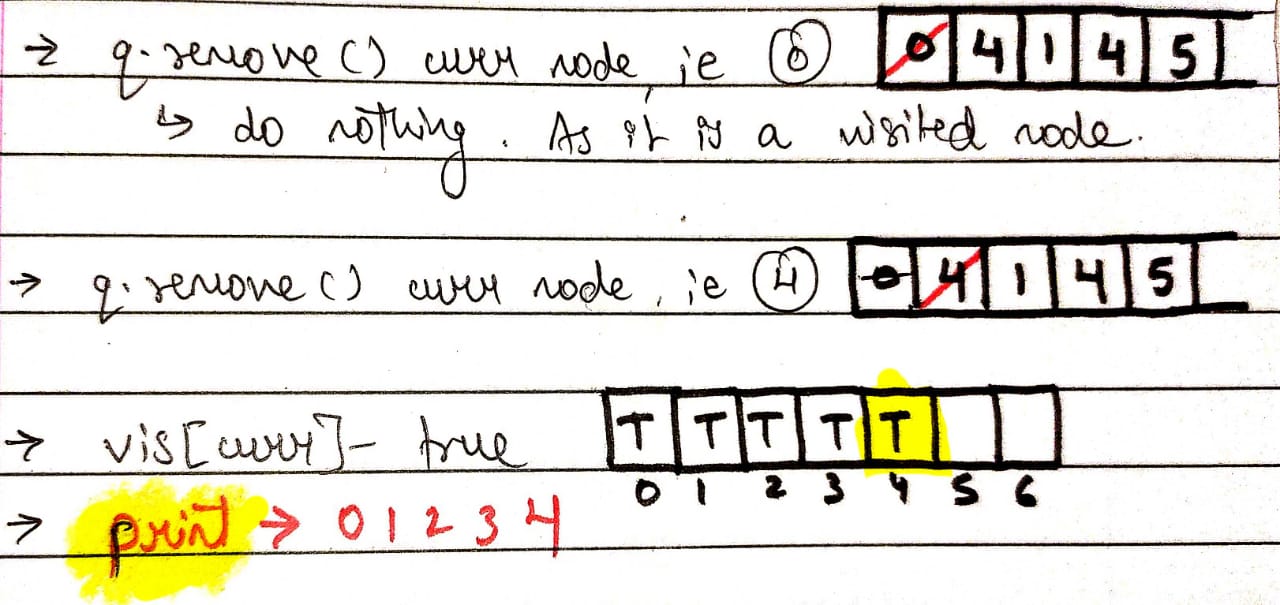
now q.remove() the curr node ie 6

mark it vis[curr] - true. and print.

by adding the neighbor of node 6, node 5 added to the queue

Simply do q.remove() for curr node 5 and as it is already visited, do nothing.

Step 4 - When the queue becomes empty, bfs is done!

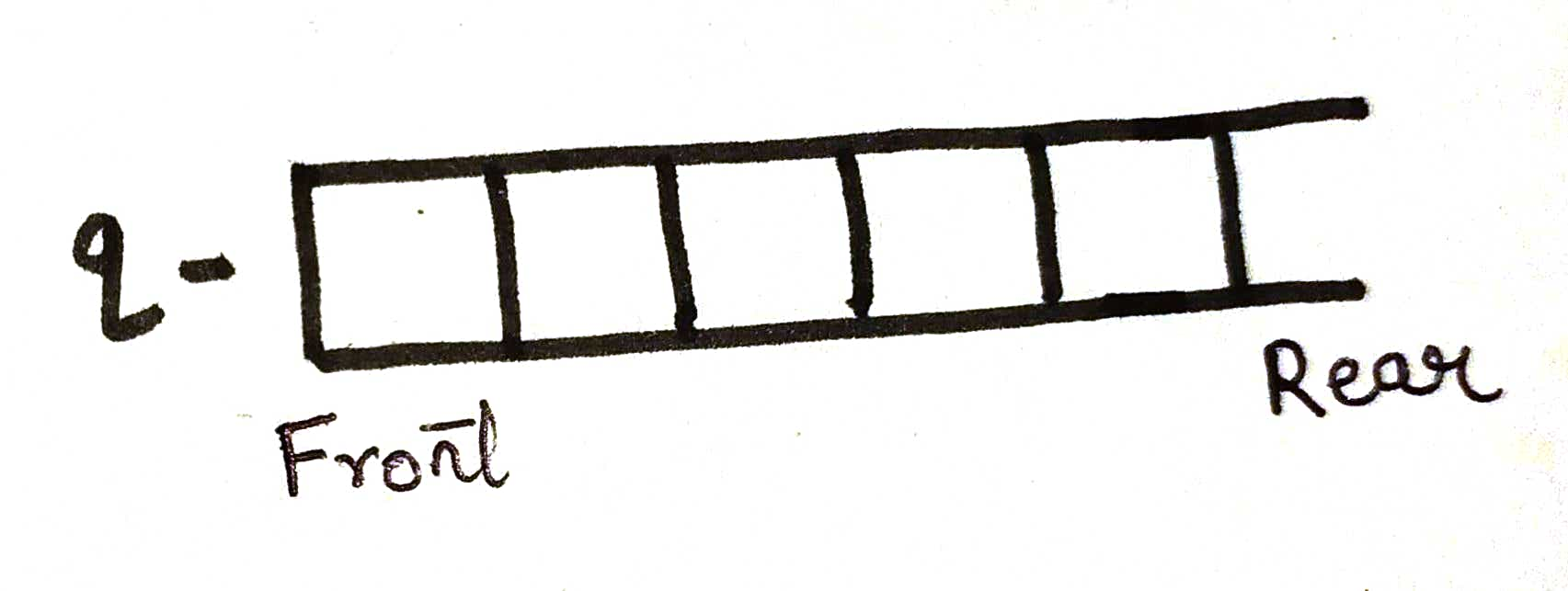
the final queue will look like this -

output:- 0 1 2 3 4 5 6

---

Depth-First Search -

Let's dive into an example as we did above

Consider DFS as Digging Floor, I know I know! please bear with me for a while😅.

Imagine you just got to know about a treasure🎁 that is 30ft below where you're standing right now😵. Now you just start digging and digging, and digging until you get it. Then you turn around (backtrack) and follow another path until you reach the end again.

That's basically what DFS is all about. It's like following the branches of a tree🌴 and going as up as you can to get a good view😁 of your neighborhood. Then you turn around and follow another branch (path) until you reach the end. You keep doing this until you finally reach the very top of the tree.

And don't forget to keep the track of your visited path (nodes) to avoid the loophole.

Algorithm:

Step 1- Here we do recursion that uses stack implicitly.

Step 2 - Create an array list to track the visited nodes.

Step 3 - If the node is un-visited ie, false (by default)

a. Print the node: print

b. Mark it visited vis[curr] = true

Step 4 - Check for all the neighbors

if the node is un-visited -> print and vis[curr] - true

else -> do nothing

Step 5 - If all the neighbors are visited then backtrack.

return

Considering the same graph of bfs here also, so that we can differentiate better:-

Dry run :-

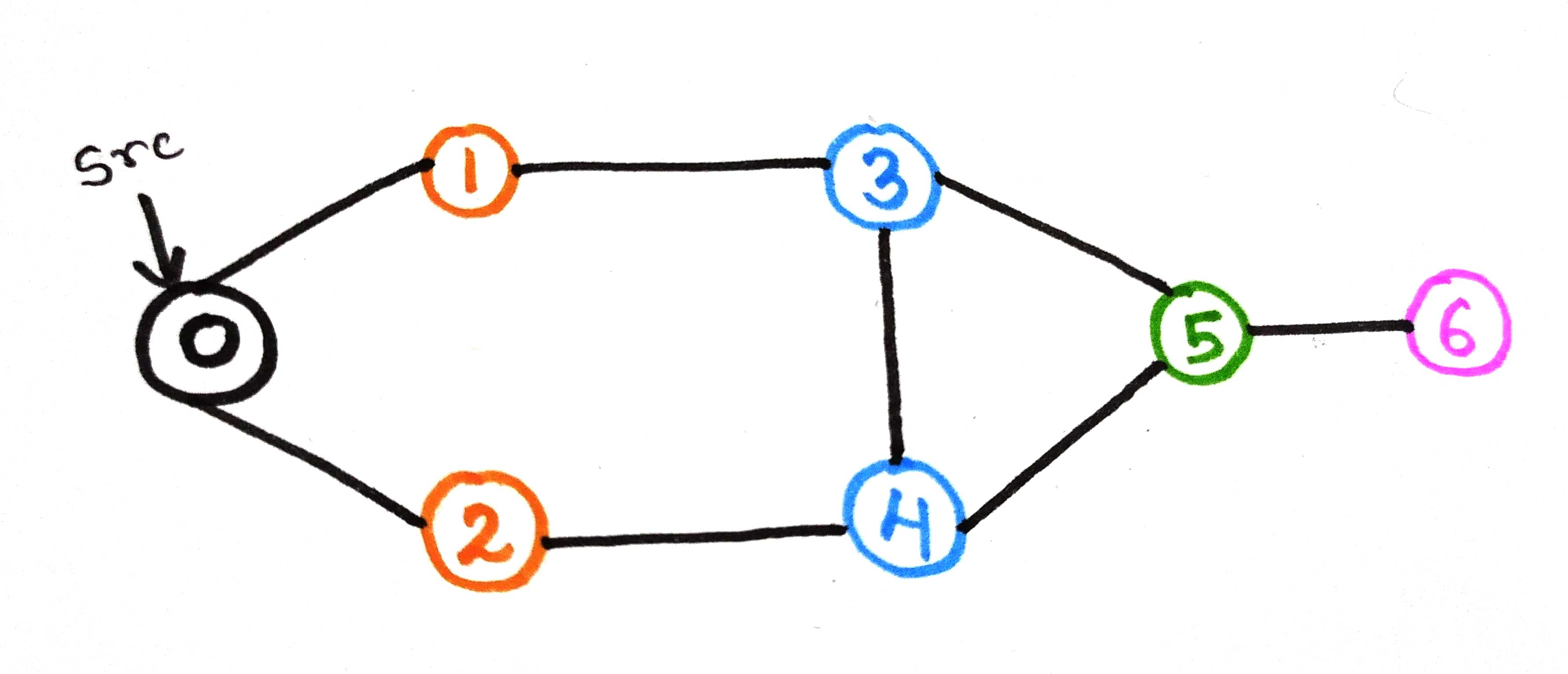
Let's take node 0 as our source node

As we're using recursion and the node is not visited, it will go inside the stack s,

Print the current node 0 and mark it as visited ie, true

Now, visit all the 0's neighbors ie, node 1 and node 2.

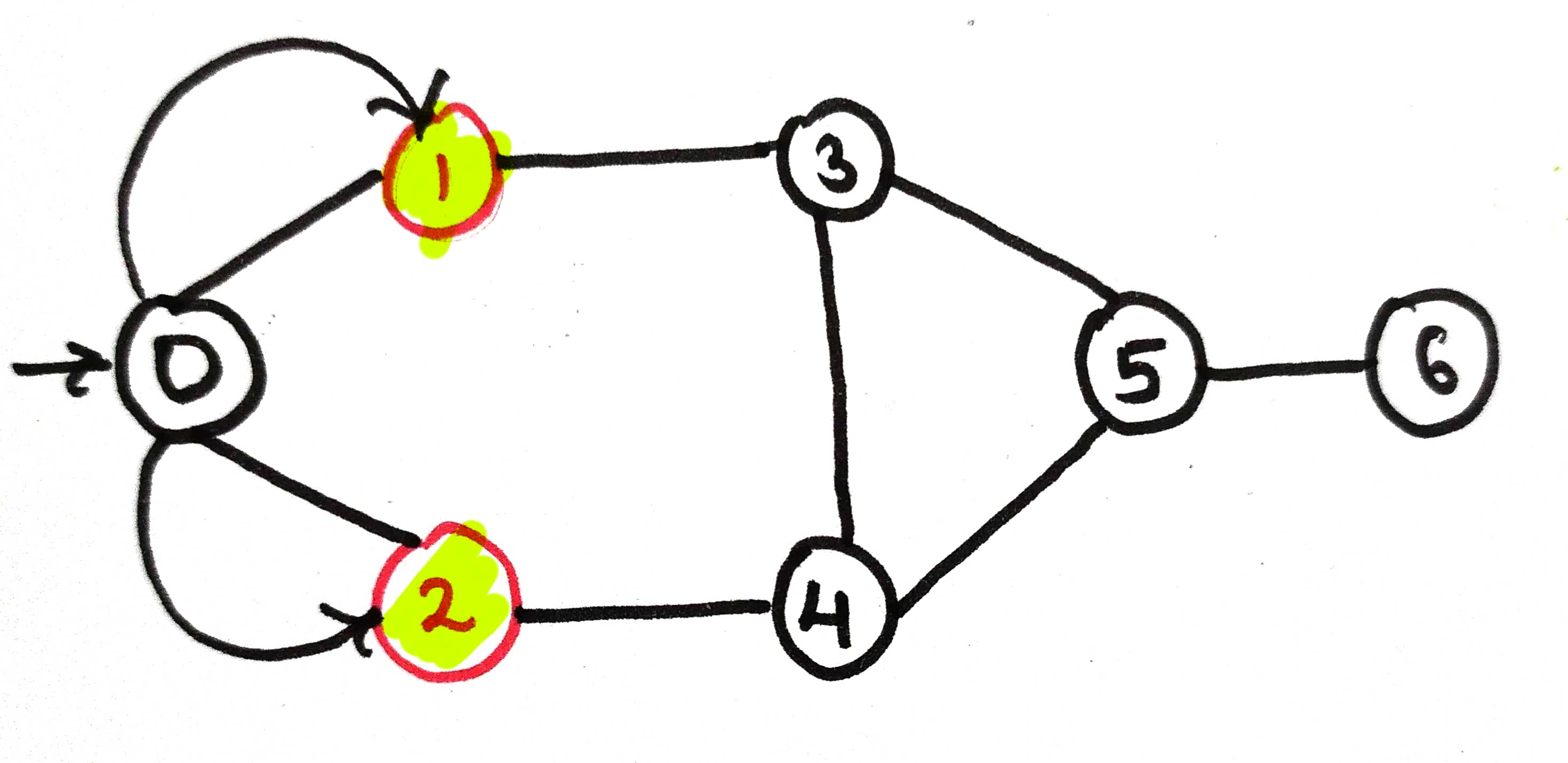
The recursion call goes for node 1 and it will be added to the stack

Print the current node 1 and mark it as visited true

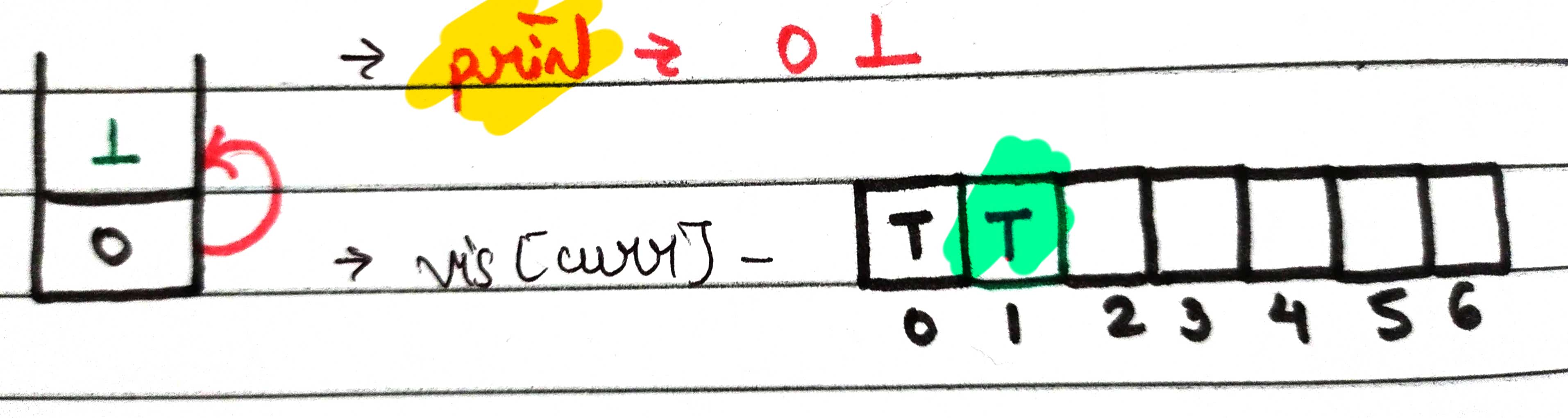
As we're on node 1, it will look for its neighbors ie, node 0 and node 3

here, node 0 is already visited so it will not go inside the stack again and won't be printed twice. The next neighbor of node 1 is node 3, so it will call node 3 .

Print the current node 3 and mark it as visited true.

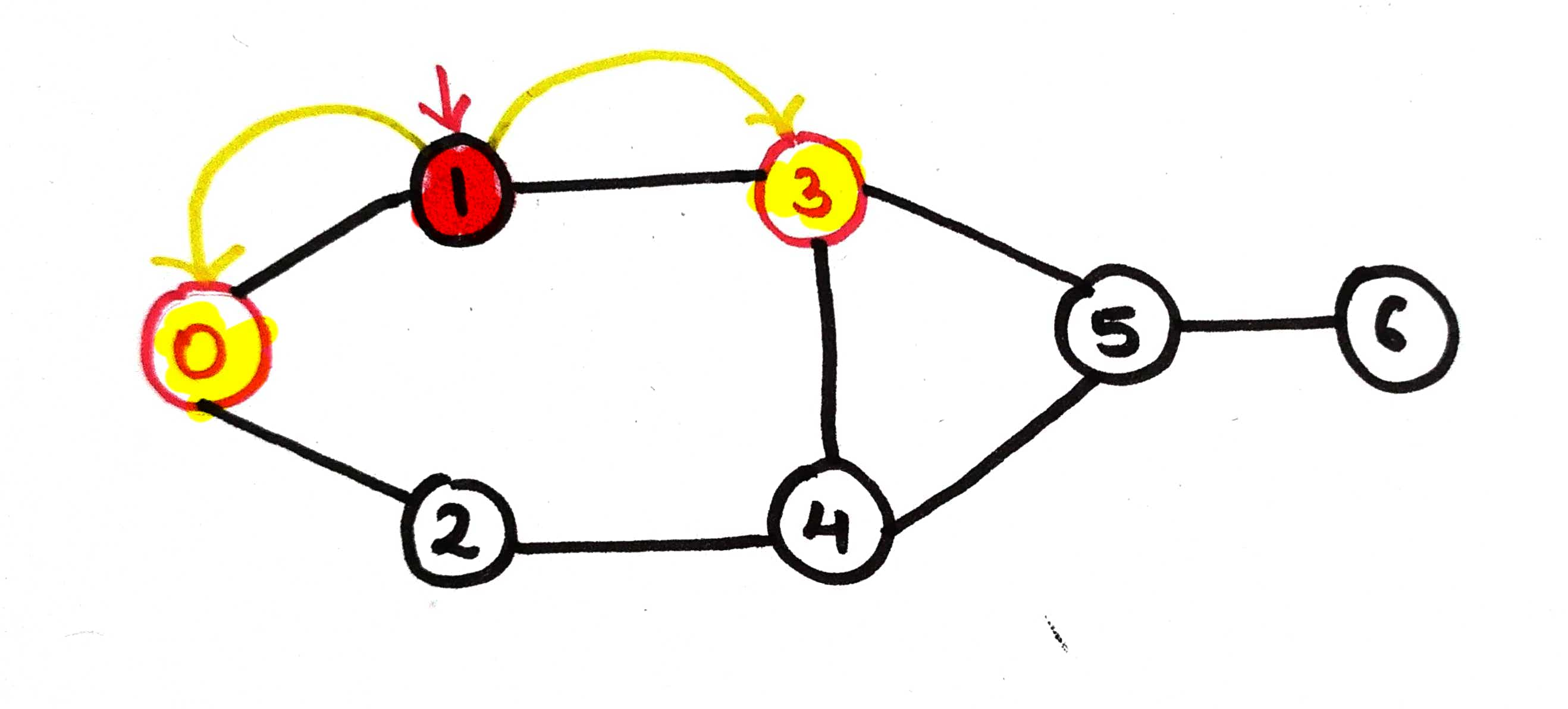
Now, we're on node 3, so it will visit all the neighbors ie, node 1, node 4 and node 5

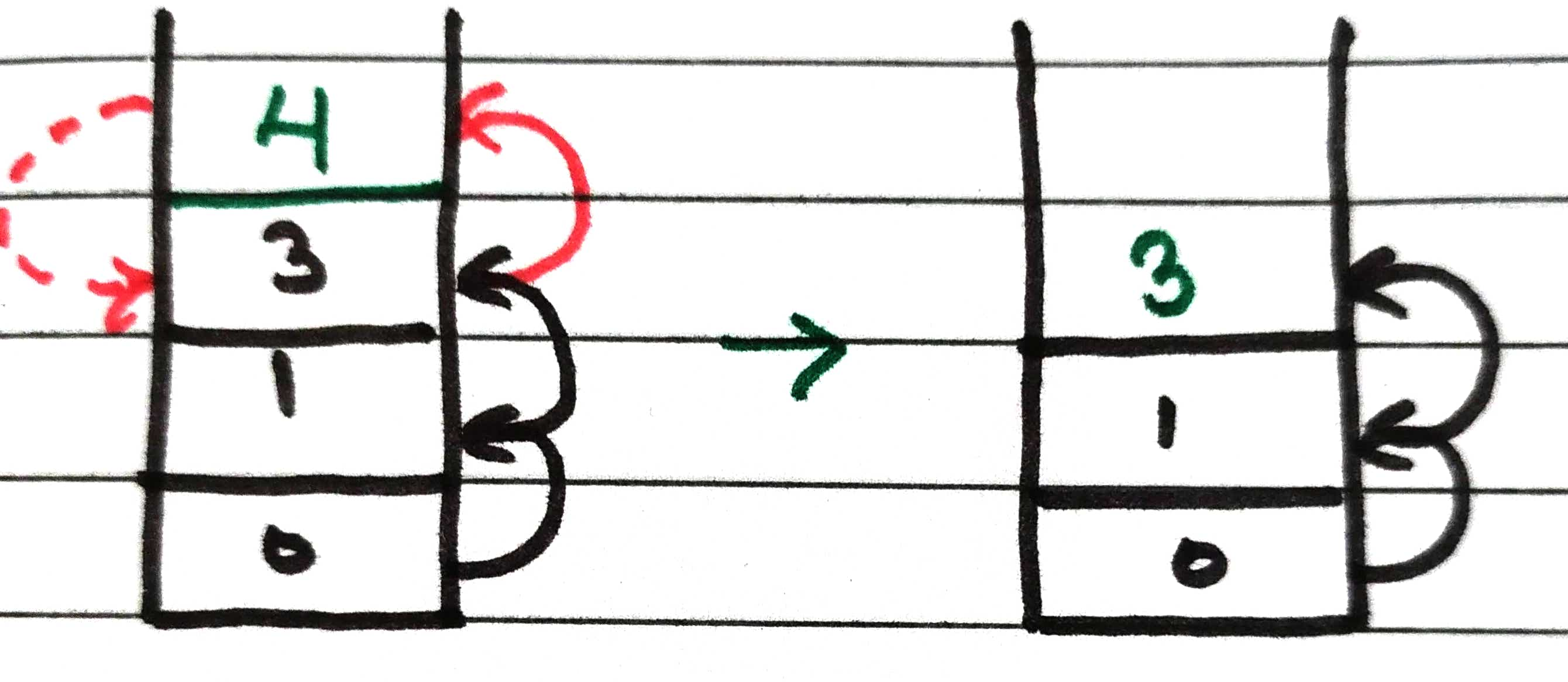
As node 1 is already visited, the call will go for the node that is node 4.

Print the current node 4 and mark it as visited true.

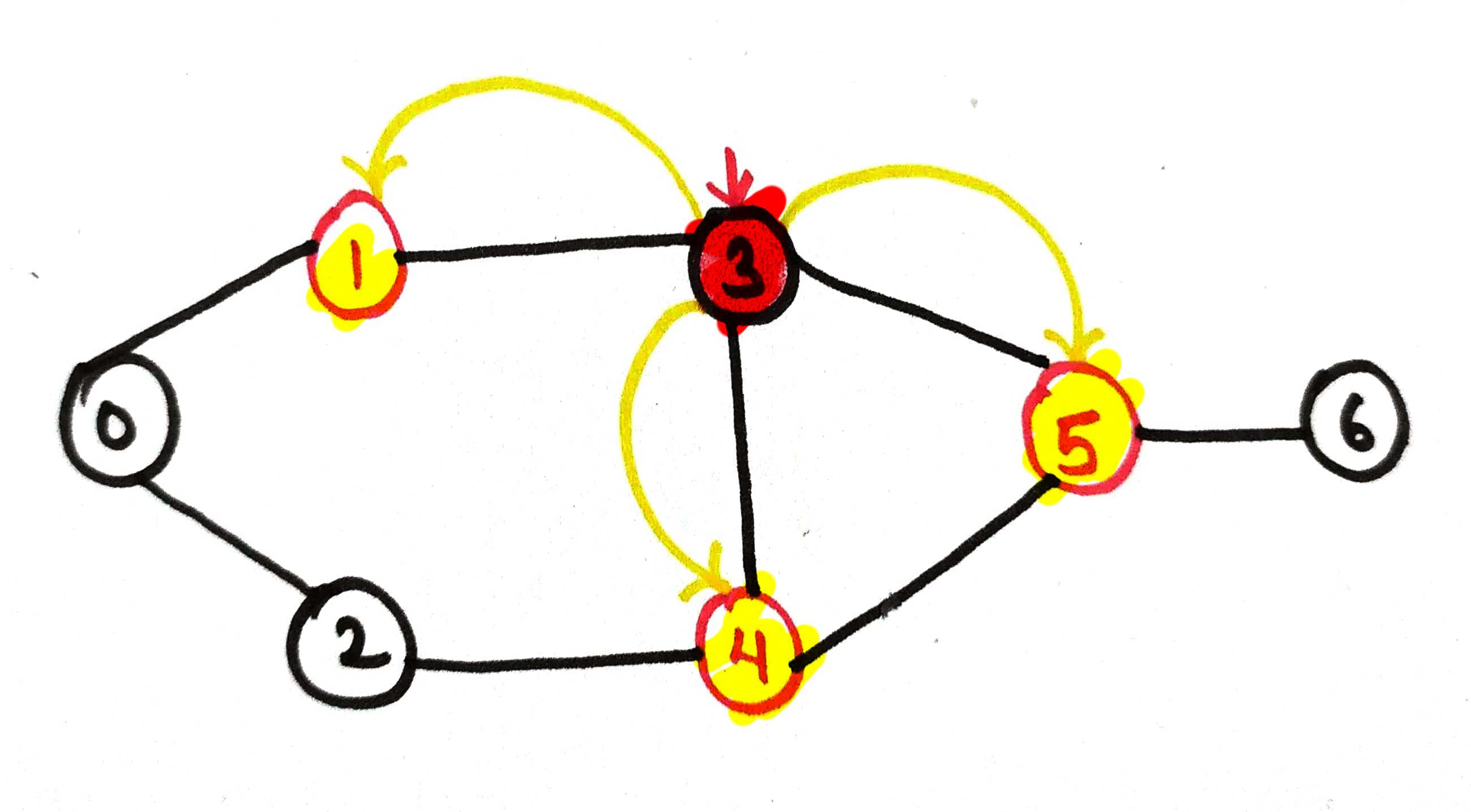
Now, we're on node 4, it will visit the neighbors ie, node 2, node 3 and node 5

The call will go for node 2 so it will be added to the stack

Print the current node 2 and mark it as visited true.

As we're on node 2, it will check for all the un-visited neighbors

here, all the neighbors are visited ie, node 0 and node 4.

So backtrack occurs and node 2 will be removed from the stack

Now, node 4 will check for its leftover neighbor ie, node 3 which is already visited.

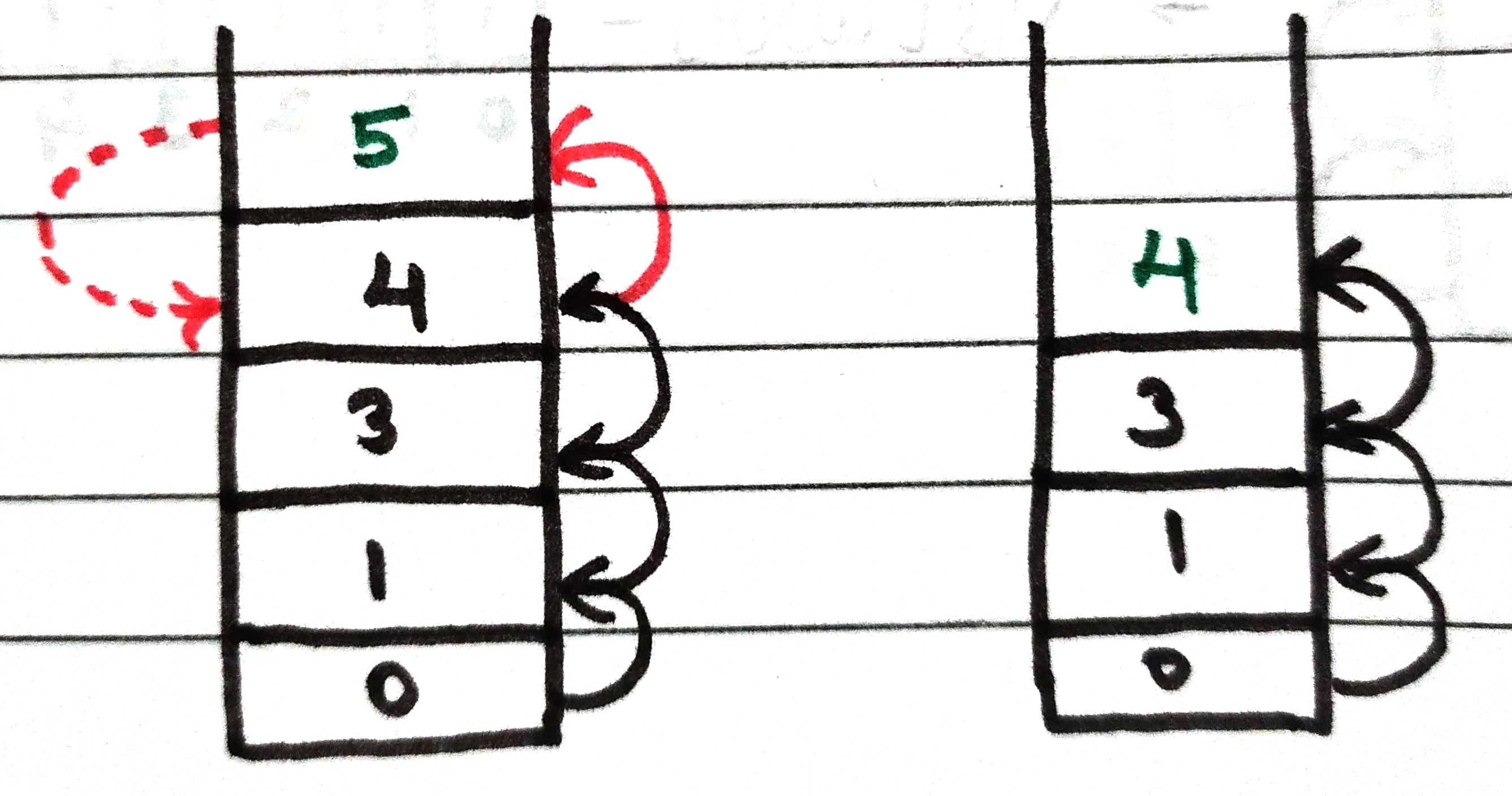
So the next call it will make is for node 5 .

Print the current node 5 and mark it as visited true.

As of now, we're on node 5, it will check for the neighbors ie, node 3, node 4 and node6

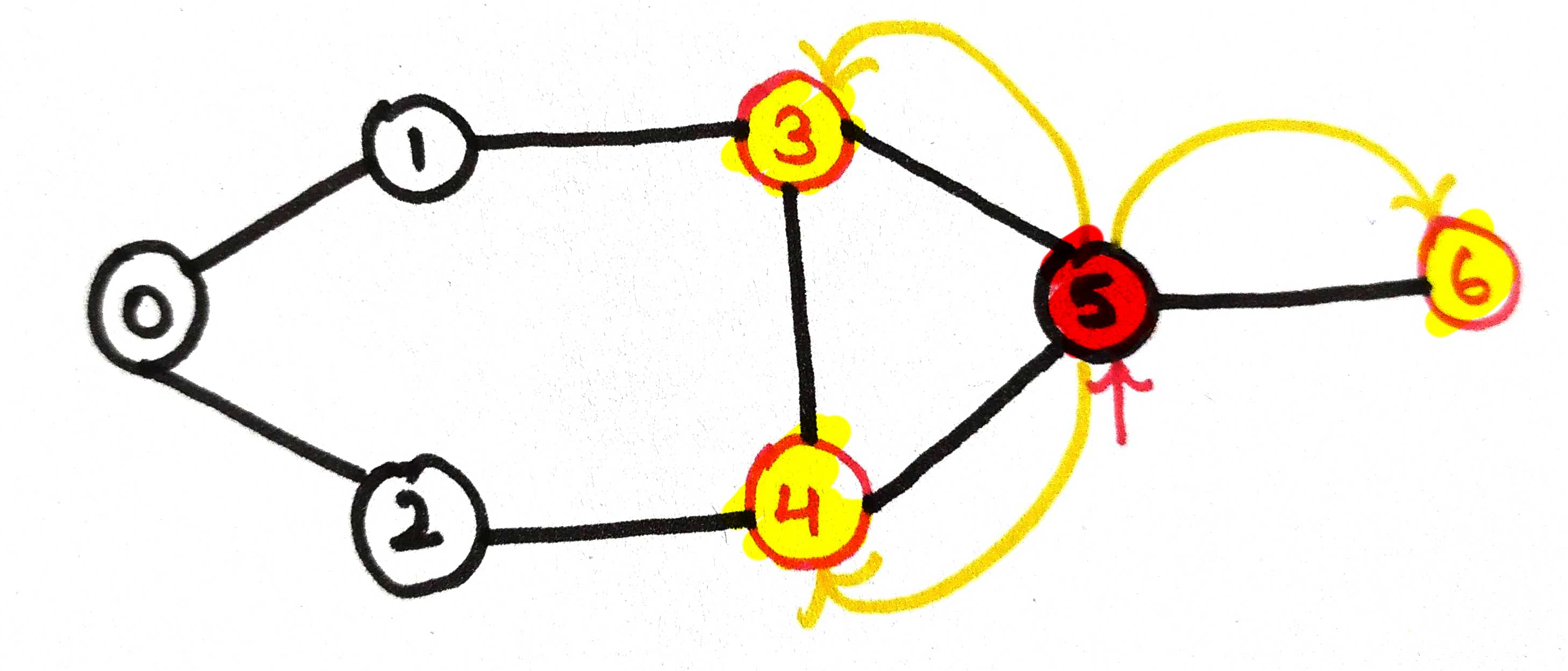
here, node 3 and node 4 both are visited already so it will call for node 6 .

Print the current node 6 and mark it as visited true.

Now, we're on node 6, it will check all the neighbors of itself.

the neighbor of node 6 is node 5 which is already visited.

So it will simply return from the stack.

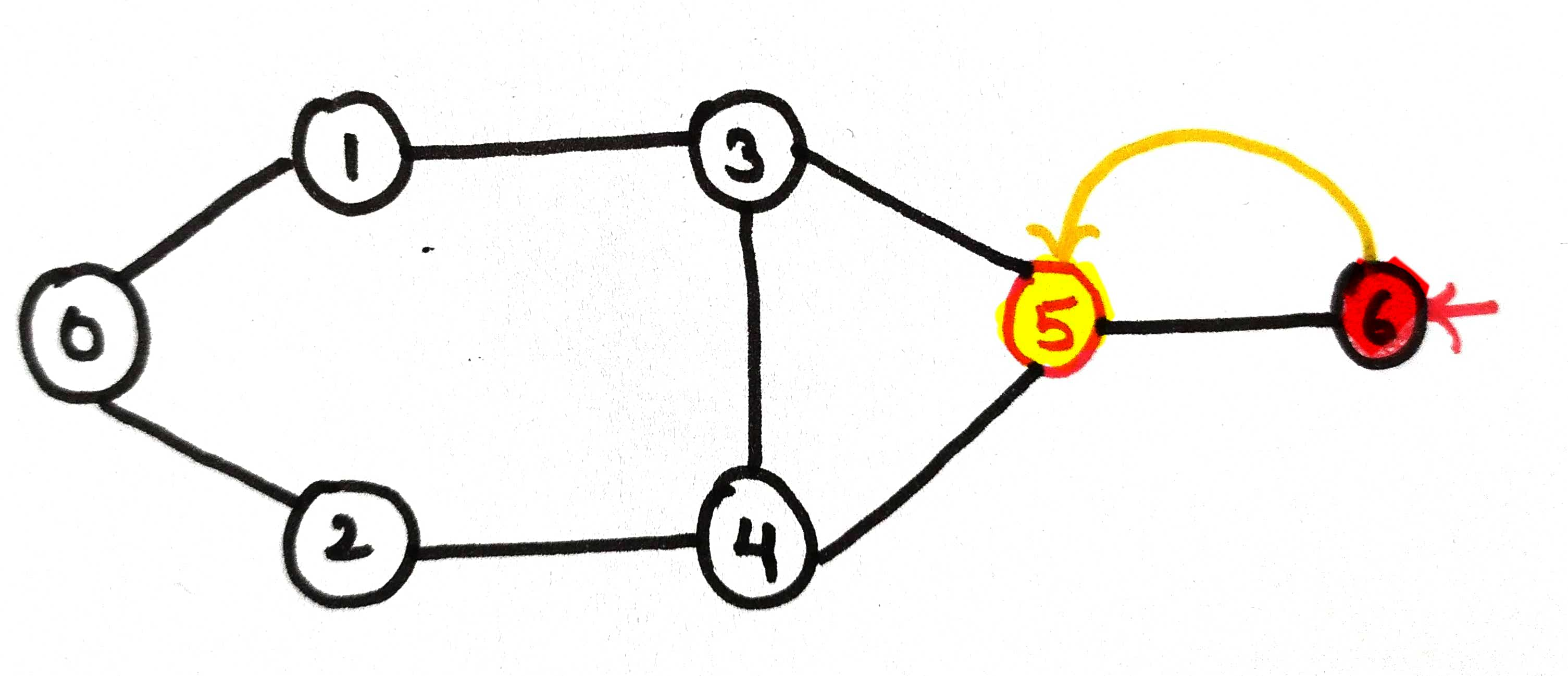
Now, node 5 will check for its un-visited node.

In this case, there is no node left out to visit. So it will be removed from the stack.

Now node 4, there is nothing left to visit, so return.

Also for now node 3, simply return from the stack as no neighbor left un-visited

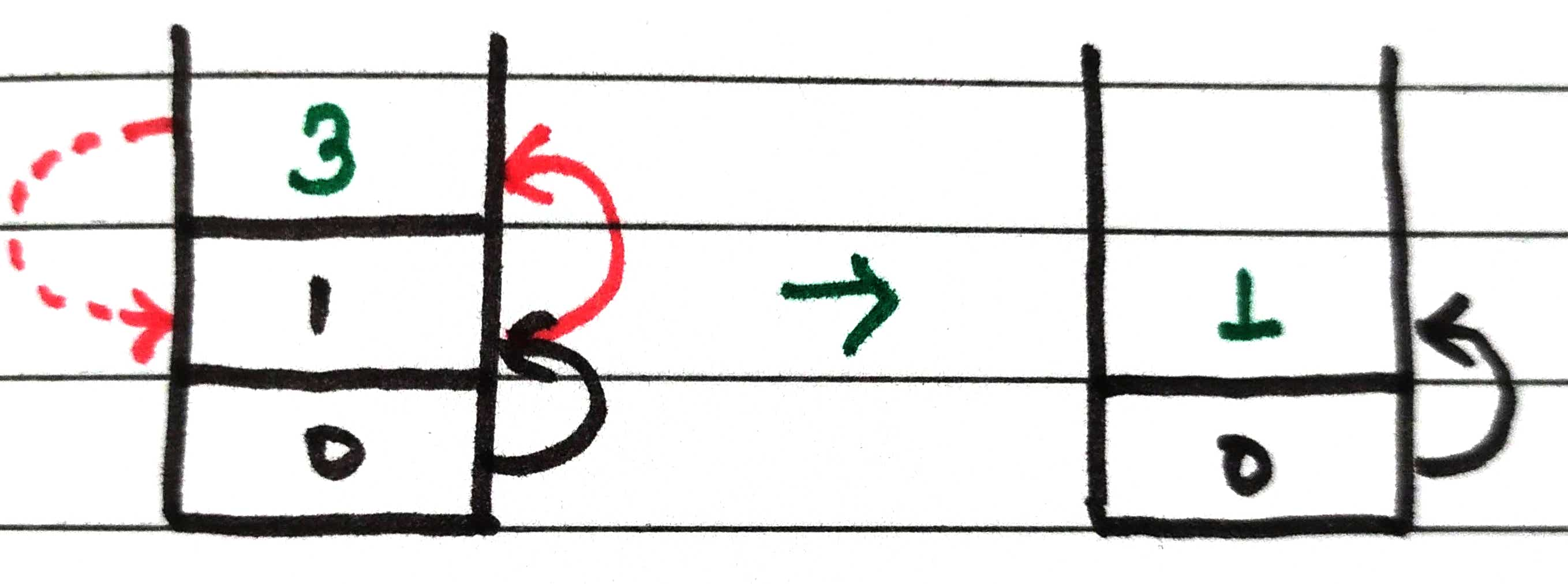
The same procedure follows for node 1 and it will be removed from the stack

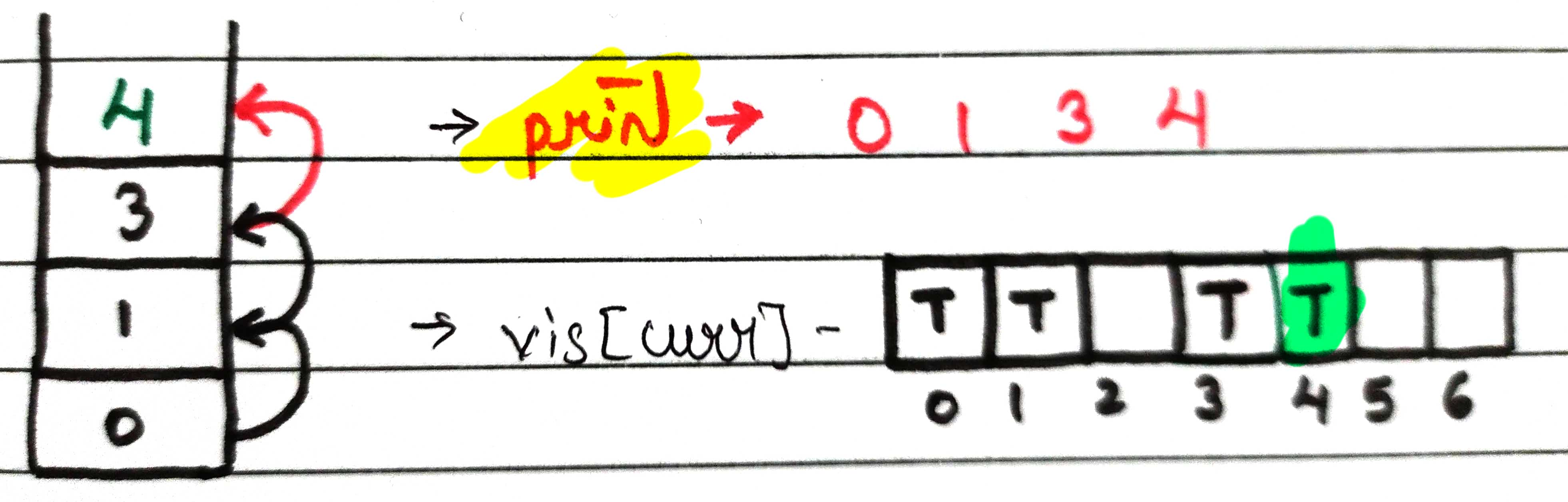
Now the last node in the stack here is node 0, check for an un-visited neighbor, and if nothing is left then simply return from it.

So, stack s will become empty.

So, our final output will print -> 0 1 3 4 2 5 6.

---

Pseudocode BFS:

function bfs( graph, node )
  stack = new Queue()
  queue.enqueue( node )

  while (queue.notEmpty())
    currentNode = queue.dequeue()

    if (!currentNode.visited)
      currentNode.visited = true

      while ( child = graph.nextUnvisitedChildOf( node ) )
        queue.enqueue( child )

Java Code:

import java.util.ArrayDeque;
import java.util.Deque;
import java.util.List;

public class BFS {

    public void search(List<List<Integer>> graph, boolean[] visited, int start) {
        Deque<Integer> queue = new ArrayDeque<>();
        visited[start] = true;
        queue.add(start);

        while (!queue.isEmpty()) {
            int vertex = queue.poll();
            for (int neighbor : graph.get(vertex)) {
                if (!visited[neighbor]) {
                    visited[neighbor] = true;
                    queue.add(neighbor);
                }
            }
        }
    }
}

---

Pseudocode DFS:

function dfs( graph, node )
  stack = new Stack()
  search(node)

  function search( node )
    if ( !node )
      return

    if ( !node.visited )
      stack.push( node )
      node.visited = true

    if ( graph.nodeHasUnvisitedChildren( node ) )
      search( graph.nextUnvisitedChildOf( node ) )
    else
      search( stack.pop() )

Java Code:

import java.util.List;

public class DFS {

    public void search(List<List<Integer>> graph, boolean[] visited, int vertex) {
        visited[vertex] = true;
        for (int neighbor : graph.get(vertex)) {
            if (!visited[neighbor]) {
                search(graph, visited, neighbor);
            }
        }
    }
}

(Source: Visual-Graph-Algorithm)

---

Interesting Facts💡:

BFS -

• BFS was first described by E.F. Moore in a paper published🧾 in 1959, where it was used to find the shortest path between two vertices in a graph.

• In fact, the famous mathematician Leonhard Euler used a similar technique in the 18th century to solve the famous Seven Bridges of Königsberg problem, which asked whether it was possible to walk through the city of Königsberg⛳ (now Kaliningrad) and cross each of its seven bridges exactly once.

• Euler's solution involved representing the city as a graph and using a breadth-first search to determine whether a solution was possible.

Use Cases:

• BFS is often used to solve puzzles🧩 that involve searching for a particular state, such as finding a solution to a maze or solving a word ladder🔢.

• It can be used in networking🌐 to find all the reachable nodes in a network or to find the shortest path between two nodes in a network.

• It can be used to test whether a graph📈 is bipartite or not. A graph is bipartite if it can be divided into two sets of vertices such that every edge connects a vertex in one set with a vertex in the other set.

DFS -

• DFS has been used in the field of psychology🧠 to study how people process and organize information.

• In one study, researchers used DFS to investigate how people👨‍👨‍👧‍👧 categorize words based on their meaning. They found that people tend to organize words into categories based on their common properties, rather than their characteristics and that this process follows a DFS pattern.

• This suggests that DFS may be a fundamental cognitive process that is used to understand and organize the world🌎 around us.

Use Cases:

• Tarjan used DFS to develop a linear-time↗ algorithm for finding the strongly connected⛓ components of a directed graph.

• It can be used to perform a topological sort on a directed acyclic graph (DAG).

• It is used in compiler design to find strongly connected components in a graph.

  ---

This blog was submitted for the "Data Structures" track-4 of the Hashnode and WeMakeDevs/CommunityClassroom December blogging challenge. Thanks to them for giving this opportunity. More blogs are coming your way of this series.

Thanks for clicking!❤️