Linear Transformation

Core concept

Transformation is another word for function. A function takes in some input, transforms it, and spits out an output. This function or transformation is represented by a matrix. To better understand it, consider the following matrix.

$$A = \left[\begin{array}{} 2 & 0 \\ 2 & 1 \\ \end{array} \right]$$

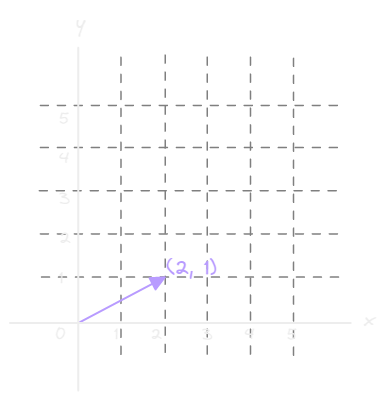
This matrix represents a certain transformation, to see it in action we can multiply it with an arbitrary vector with coordinates (2, 1)

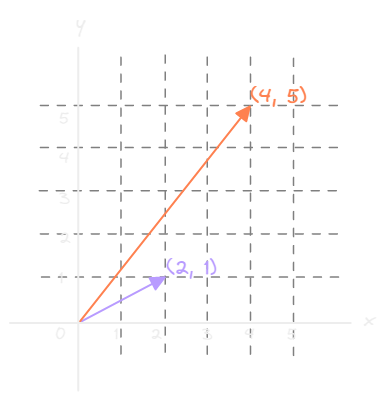
When we multiply, we get a new vector with coordinates (4, 5) as shown here

$$\left[\begin{array}{} 2 & 0 \\ 2 & 1 \\ \end{array} \right] \left[\begin{array}{} 2 \\ 1 \\ \end{array} \right] = \left[\begin{array}{} 4 \\ 5 \\ \end{array} \right]$$

And when we plot this on the graph we can see how Matrix A "transformed" the vector (2, 1) into another vector (4, 5)

This is why it represents a transformation. But what is so "linear" about it?

Linearity

For a transformation to be linear it needs to maintain the following two properties after the transformation.

1. All lines must remain straight

2. The origin must not move

Considering the example above, we can say that Matrix A can transform any vector in the 2D space into another vector. In other words, the Matrix transforms the entire plane (aka vector space) into a different one while preserving its structure.

Shear Matrix Example

A shear matrix is a special matrix that only transforms either one of the two base axes (either X or Y)

Consider a shear matrix transforming a vector with coordinates (0, 2). Numerically we can show the transformation like

$$\left[\begin{array}{} 1 & 1 \\ 0 & 1 \\ \end{array} \right] \times\left[\begin{array}{} 0 \\ 2 \\ \end{array} \right]$$

But when plotted on a graph, it becomes apparent how the transformation reshapes the vector space around it.

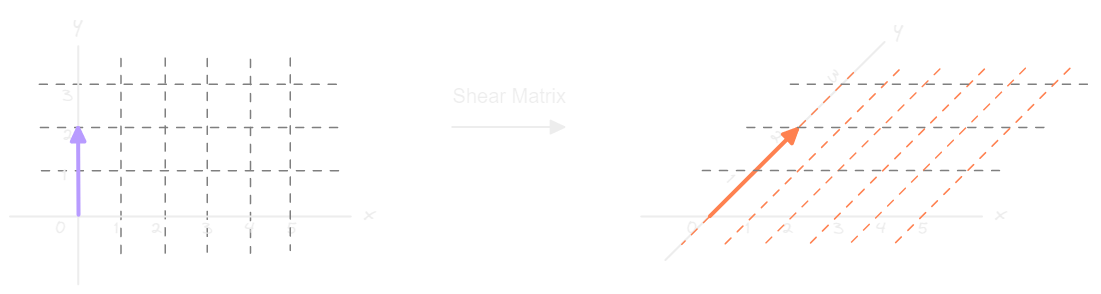
You can see in the figure above how a shear matrix transforms a vector (purple arrow) but notice that the transformation also applies to the entire vector space around it (orange arrow and lines).

1. All the [orange] lines are straight after the transformation

2. The origin has not moved

Therefore we can say that the shear matrix has "Linearly Transformed" the vector space.

Simplification

But it isn't always so convenient to imagine/draw a vector space transforming into a new shape. Instead, we focus on the input vectors and just plot how they reshape while keeping the base grid as it is. This helps us focus on how the vectors are affected and not worry about how the entire vector space transforms.

A more generalised way to measure the effect is to apply the linear transformation only to a set of unit vectors - i and j with coordinates (1, 0) and (0, 1) respectively. And the whole grid of the vector space would basically follow the same path

---

Thank you so much for reading! You can read the next article in the series which explains what are Determinants

If this has helped you in any form, you can show your appreciation by reacting to this article and if you have any questions or feedback please leave them in the comments below

Thanks again!