What is Word2vec?

Word2Vec is a shallow, two-layer neural network that is trained to reconstruct the linguistic contexts of words.

• It takes as its input a large corpus of words and produces a vector space, typically of several hundred dimensions, with each unique word in the corpus being assigned to the corresponding vector in space.

• Word vectors are positioned in a vector space such that words that share common contexts in the corpus are located close to one another in the space.

• Word2Vec is a particularly computationally-efficient predictive model for learning word embeddings from raw text.

• Word2Vec is a group of models that helps derive relations between a word and its contextual words.

• Let’s look at two important models inside Word2Vec: Skip-grams and CBOW.

Skin-grams:

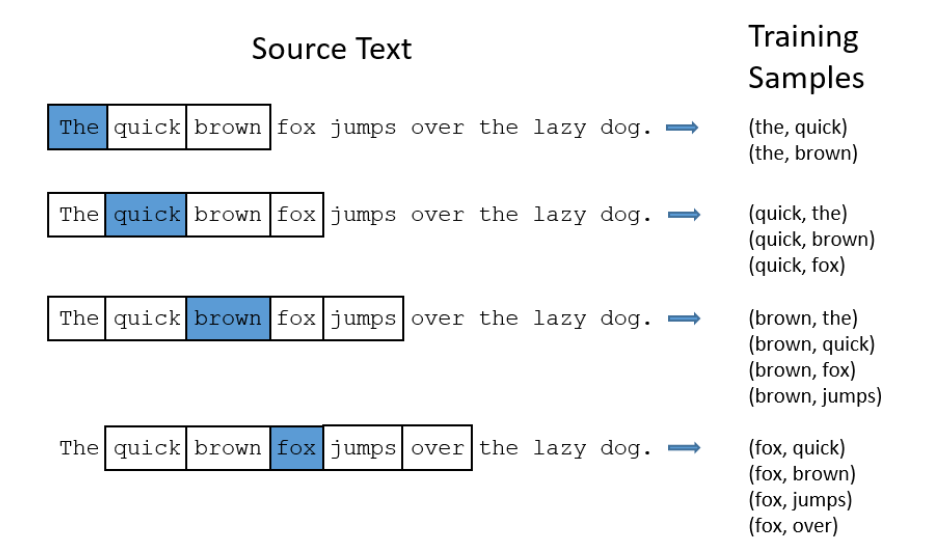
• In the Skip-gram model, we take a center word and a window of context (neighbor) words, and we try to predict the context of words out to some window size for each center word.

• So, our model is going to define a probability distribution, i.e. probability of a word appearing in the context given a center word and we are going to choose our vector representations to maximize the probability.

Continuous Bag-of-Words (CBOW):

CBOW predicts target words (e.g. ‘mat’) from the surrounding context words (‘the cat sits on the’).

• Statistically, it affects that CBOW smoothes over a lot of distributional information (by treating an entire context as one observation). For the most part, this turns out to be a useful thing for smaller datasets.

This was about converting words into vectors. But where does the “learning” happen?

Essentially, we begin with small random initialization of word vectors. Our predictive model learns the vectors by minimizing the loss function. In Word2vec, this happens with feed-forward neural networks and optimization techniques such as Stochastic gradient descent.

• There are also count-based models which make the co-occurrence count matrix of the words in our corpus; we have a very large matrix with each row for the “words” and columns for the “context”.

• The number of “contexts” is, of course very large, since it is very essentially combinatorial in size.

• To overcome this issue, we apply SVD to a matrix.

• This reduces the dimensions of the matrix to retain the maximum number of pieces of information.