Hui!!

Euclid's Algo

Let's start with GCD(Greatest Common Divisor). I would assume you know what GCD is. You might know different ways to calculate GCD. You might use Euclid's Algo to find the GCD of two numbers or you would just represent both numbers in their prime factors and check for all the common factors. Either way, you will get the same result.

So,

Just to demonstrate, I will give you an example of how to calculate the GCD of two numbers. I will do it as one will do it on paper, but the same idea could be extrapolated to build working code.

NOTE: The division algorithm is just writing any number in the form

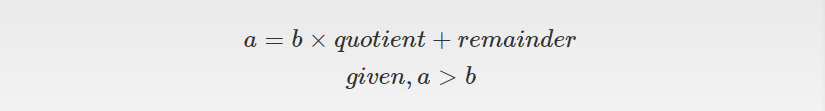
$$\displaylines{ \text{GCD of two numbers 10 and 16} \newline \text{we will write the bigger number with the use of division algorithm} \newline 16 = 10 \times (1) + 6 \newline 10 = 6 \times (1) + 4 \newline 6 = 4 \times (1) + 2 \newline 4 = 2 \times (2) + 0 \newline \text{GCD of two numbers is always the last non-zero remainder} \newline \text{Hence, the GCD is } 2 }$$

I guess you already know this algorithm. This is called Euclid's Algorithm. We can easily prove why the idea works. Let's dive into its proof first. Then we will later look at its applications.

GCD is the last non-zero remainder

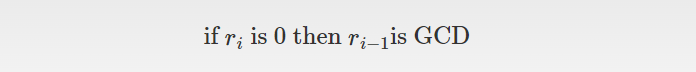
The very first thing to prove here is that

$$\displaylines{ if \space a = b \times q + r \newline \text{ then GCD(a, b) = GCD(b, r)} \newline }$$

For now, let us assume that it is true (later we will prove it), and let's go ahead and just look at the last condition.

$$\begin{align} & a = b \times q + r \newline & \text{We know GCD(a, b) = GCD(b, r)} \newline & b = r \times q_1 + r_1 \newline & \text{We continue to do that and at the end, we have r = 0} \newline & \text{Now for this condition we have new } a_i \space and \space new \space b_i \newline & \text{Now } a_i \text{ can be represented as } a_i = b_i \times q \text{ (as r = 0)} \newline & \text{It is not very hard to see if } b_i \text{ is multiple of } a_i \text{ then} \newline & \text{GCD of } a_i \space and \space b_i \text{ is } b_i \newline \end{align}$$

Now, let's prove the first condition.

$$\begin{align} & \text{Assume g is the common divisor of a and b} \newline & \text{It means we can write, } \newline & a = k_1 \times g \newline & b = k_2 \times g \newline & \newline & \text{We can also prove that g is also the factor of a - b} \newline & a - b = k_1 \times g - k_2 \times g \newline & \space \space \space \space \space \space \space \space \space = (k_1 - k_2) \times g \newline & \newline & \text{Now, } k_1 \text{ and } k_2 \text{ are both integers so } k_1 - k_2 \text{ is also integer} \newline & \text{Hence, g is divisible to a - b} \newline & \text{Now, we can also prove that g is factor of any multiple of b.} \newline & \text{So, } a - k \times b \text{ is also divisible by } g \newline \end{align}$$

Now, using all we proved earlier;

NOTE: g | a is a notation that denotes "g divides a" or "g is a factor of a"

$$\begin{align} & \text{g | a } \newline & \text{g | b} \newline & \text{g | (a - b)} \newline & \text{g | } (a - k \times b) \newline \end{align}$$

Using the above equations,

$$\begin{align} & a = b \times q + r \newline & a - b \times q = r \newline & \text{We, just prove that } a - b \times q \text{ is also divislbe by g} \newline & \text{So, r is also divisible by g} \newline & \text{So, we prove that GCD(a, b) = GCD(b, a % r)} \newline \end{align}$$

NOTE: a % b indicates the remainder when b divides a.

That was proof of Euclid's Algorithm. If you have any doubts about a particular step you can ask in the comments or leave a message.

Now, for the coding part, we can use this as follows

$$\begin{align} \text{Now, GCD(a, b) = GCD(b, a % b)} \end{align}$$

We can recursively call this function until one of them becomes 0.

int gcd(int a, int b) {
    if(b > a) {
        swap(a, b);
    }
    if(b == 0) {
        return a;
    }
    return gcd(b, a % b);
}

We usually use the inbuilt __gcd function in C++.

---

Extended Euclidean Algorithm

We can use "Extended Euclid's Algorithm" to solve linear diophantine equations. Diophantine equations are polynomial equations in two or more variables. Linear diophantine equations are of the type,

$$a . x + b. y = c$$

Now, as per Bézout's identity, the integral solutions of x and y exist only if GCD(a,b) divides the c.

The proof of that is pretty simple,

$$\begin{align} & \text{If g is GCD of a and b} \newline & a = g \times k_1 \newline & b = g \times k_2 \newline & g \times k_1 . x + g \times k_2 . y = c \newline & g \times (k_1.x + k_2.y) = c \newline & \text{So for } (k_1.x + k_2.y) \text{ to be an integer } \frac{c}{g} \text{ must be an integer.} \end{align}$$

We can solve many equations like this, using GCD.

$$\begin{align} a.x + b.y = GCD(a, b) \end{align}$$

Using Euclid's Algorithm,

$$\text{GCD(a, b) = GCD(b, a % b)}$$

So, we can also have another equation of the form

$$\begin{align} & b.x_1 + \text{(a % b)}.y_1 = GCD(a, b) \end{align}$$

We can expand the remainder as follows

$$\text{a % b} = a - \lfloor \frac{a}{b}\rfloor \times b$$

$$NOTE: \lfloor \frac{a}{b} \rfloor \text{ indicates division rounded off to lower integer.}$$

Let's use this in the above equation,

$$\begin{align} & b.x_1 + (a - \lfloor \frac{a}{b}\rfloor . b).y_1 = GCD(a, b) \newline & b.x_1 + a.y_1 - \lfloor \frac{a}{b}\rfloor.b.y_1 = GCD(a, b) \newline & a.y_1 + (x_1 - \lfloor \frac{a}{b} \rfloor .y_1).b = GCD(a, b) \newline \end{align}$$

Compare this equation with

$$a.x + b.y = GCD(a, b)$$

We can now see that the value of x and y can be obtained by comparing the value of the coefficient of a and b.

$$\begin{align} & x = y_1 \newline & y = x_1 - \lfloor \frac{a}{b} \rfloor. y_1 \end{align}$$

We can use this in code as follows,

#include<bits/stdc++.h>
using namespace std;

class Variables
{
public:
    int x, y;
    int g;
};

Variables extendedGCD1(int a, int b) {
    Variables ans;
    if(b == 0) {
        ans.x = 1;
        ans.y = 0;
        ans.g = a;
        return ans;
    }

    Variables temp = extendedGCD1(b, a % b);
    ans.x = temp.y;
    ans.y = temp.x - (a / b) * temp.y;
    ans.g = temp.g;
    return ans;
}

int main() {
    int a, b;
    cin >> a >> b;

    Variables ans = extendedGCD1(a, b);

    cout << "The GCD of a and b is " << ans.g << endl;
    cout << "The values of x: " << ans.x << " y: " << ans.y << endl;
    return 0;
}

Let us look at the base case (when b == 0).

$$\begin{align} & \text{When b = 0 and } a.x + b.y = GCD(a, b) \newline & a.x + 0.y = GCD(a, 0) \newline & a.x = a \newline & Hence, \space x = 1, y = 0, g = a \end{align}$$

The better way to code this is to pass parameters X and Y as reference. So after you call the function you can get the values of X and Y modified.

int eucledianGCD(int a, int b, int &X, int &Y) {
    if(b == 0) {
        X = 1;
        Y = 0;
        //We are returing GCD from functions
        //And values of X and Y are modified
        return a;
    }

    int g = eucledianGCD(b, a % b, X, Y);
    int tempX = Y;
    int tempY = X - (a / b) * Y;
    X = tempX, Y = tempY;
    return g;
}

---

Multiplicative Modulo Inverse

In mathematics, the multiplicative inverse of a number is just:

$$\displaylines{ & A.B = 1 \newline & B = \frac{1}{A} \newline & \text{So, } \frac{1}{A} \text{ is the multiplicative inverse of A.} \newline }$$

In, modular arithmetic the concept is the same but with modulus on both sides.

$$\begin{align} & \text{(A.B) % m = 1 % m} \newline & \text{It just means when m divides A.B it leaves 1 as a remainder} \newline & \text{We can write: m | (A.B - 1)} \newline & A.B - 1 = m.k \newline & A.B - m.k = 1 \newline & A.(B) + m.(-k) = 1 \newline & \text{We know, A and m are known, We can consider B and } -k \text{ as variable x and y} \newline & \text{So, we again have the same equations as earlier} \newline & A.x + m.y = 1 \newline \end{align}$$

We can use an extended euclidean algorithm to find the values of x and y, meaning we can find the values of B and k. Hence, we can find the modulo inverse of the number A.

One more thing to notice here, as Bézout's identity says the integer values of x and y will only exist if GCD(A, b) divides c (in this case c = 1). So, GCD(A, m) must divide c (c = 1). As 1 can not have any other factor other than 1, GCD(A, m) should be equal to 1 for the inverse of A with modulo m to exist. i.e. A and m should be coprime.

NOTE: This is the reason why we are always given answer % prime numbers to calculate in competitive programming. GCD(prime, any_number) is always 1.

The following code can be used to find the modulo inverse of the number:

int getModuloInverse(int num, int mod) {
    if(__gcd(num, mod) != 1) {
        cout << "Inverse doesn't exist" << endl;
        return -1;
    }

    int inverse, q;
    eucledianGCD(num, mod, inverse, q);
    return inverse;
}

---

Problems

Problem 1

To be continued....