Introduction

I encountered Pharo in the process of trying to find an interesting project to contribute to in the open-source community space. I will write a separate blog on How I came across the Pharo Community and Why I started learning such a niche language.

What is Pharo??

Pharo is an open-source Smalltalk-inspired programming language and development environment. It is designed to be simple, elegant, and easy to learn and use, and it has a strong emphasis on object-oriented programming.

So, the main purpose of this blog is to present a small program that I have written to familiarise myself with Pharo which is "Implementation of a simple Linked List and a basic Complete Binary Tree."

Linked List

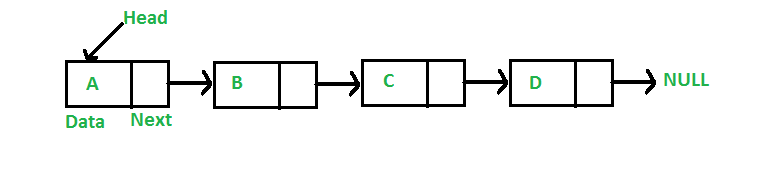
It is important to understand what is a linked list before going on to Binary Trees. So please refer to this blog for a detailed explanation. I will only go through the implementation and code of the linked list in this blog. The tests can be found in the above-linked blog. I will, however, cover basic complete binary trees in detail.

Implementation

We will start by creating our own Package called MyLinkedList and we create 2 classes inside the package.

• LLNode - This class is to represent a single Linked List Node

• LL - This class is to represent the entire Linked list

LLNode

We create the LLNode class with instance variables value and next. We start by making the class.

Object subclass: #LLNode
    instanceVariableNames: 'value next'
    classVariableNames: ''
    package: 'MyLinkedList'

We then implement the following functions :

• getter and setter functions for next (next, next:)

• getter and setter functions for value (value, value:)

• printNode function - To print the value of the LLNode

Also, note that we don't create an initialize method as in Pharo they are directly initialized to nil.

LLNode>>next

"returns the next LLnode "
    ^next

LLNode>>next: aLLNode

"Sets the next LLnode "
    next:= aLLNode

LLNode>>value 

"Returns the value of the current Node"
    ^value

LLNode>>value: anInteger

"Sets the value of the current Node"
    value := anInteger

LLNode>>printNode 

"Prints the value of the current node and returns string version of value "
    Transcript show: value asString;cr.
    ^(value asString)

LL

We now create the LL class with instance variables head. We start by making the class.

Object subclass: #LL
    instanceVariableNames: 'head'
    classVariableNames: ''
    package: 'MyLinkedList'

We then implement the following functions :

• getter and setter functions for head (LLhead, LLhead:)

• TranscriptList- to print the values of the entire list on the Transcript window

• listcollection and printList to return an OrderedCollection and String of values of the list respectively.

• appendNode to add a LLNode at the end of the Linked List

LL>>LLhead

"Returns head of the Linked List (where head is aLLNode)"

    ^head

LL>>LLhead: aLLNode

"Sets head of the Linked List"
    head := aLLNode

LL>>TranscriptList

"Shows the output on a Transcript all the values in the Linked List"

    | temp  |
    temp := head .    
    [ temp value ] 
              whileNotNil: [ Transcript show: temp value asString ;cr.
                             temp := temp next].

LL>>listcollection

"Returns a orderedCollection of all the values in the Linked List"

    | temp col |
    temp := head .
    col := OrderedCollection new.
    [ temp value ] whileNotNil: [ col add: temp value.
                                    temp := temp next].
    ^col

LL >> printList

"Returns a string of all the values in the Linked List"

    | temp str |
    temp := head .
    str := ''.
    [ temp value ] 
               whileNotNil: [ str:=(str , temp value asString , ' ') .
                               temp := temp next].
    ^str

LL>>appendNode: anInteger

"Appends(at the end) a LLnode with the value sent as sent as argument to this method "

    |newNode temp|
    temp:=head. 
    newNode:= LLNode new.
    newNode value: anInteger .
    [ temp ] whileNotNil: [ temp:=temp next ];
                ifNil: [ temp:= newNode  ].

The Test Class for the Linked List should also be implemented.

Complete Binary Trees

What are Binary Trees?

Binary Tree is defined as a tree data structure where each node has at most 2 children. The node can have 0, 1 or 2 children. Since each element in a binary tree can have only 2 children, we typically name them the left and right child.

The are many different types of Binary Trees. But we will focus on implementing the Complete Binary Tree

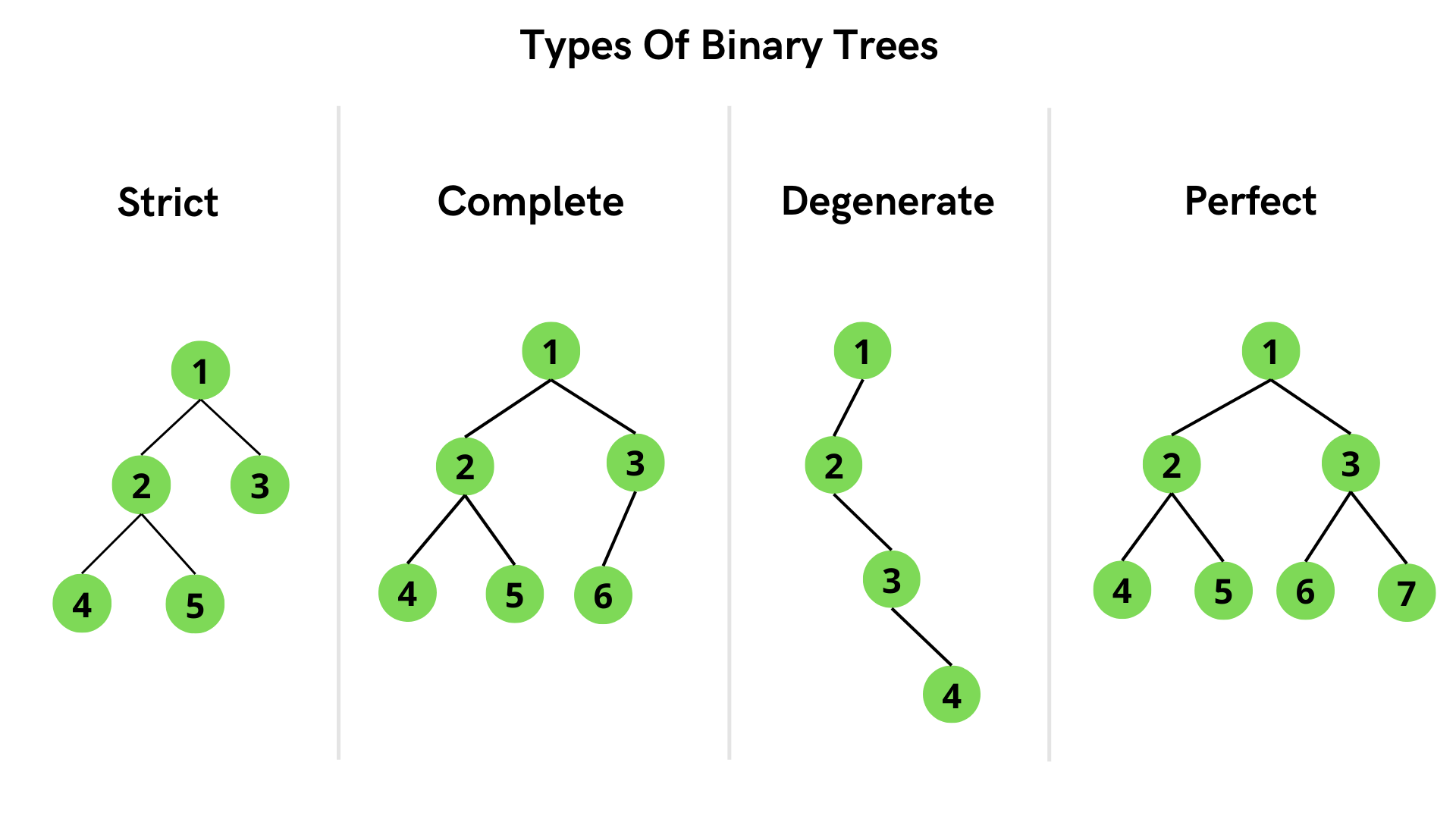
What is a Complete Binary Tree?

A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible.

The Binary tree is made up of nodes where each node consists of

• value - The Value of the node

• left - The pointer to the left node

• right - The pointer to the right node

Each node in a complete binary tree has either 0,1 or 2 children. The main node, where the tree begins is called the root node. So, in a complete binary tree, we start filling the left child of a node and then keep moving to the right child. We also need to keep in mind that all the levels except the last level need to be completely filled.

Implementation

We first create a new package called MyBinaryTree package. We create two classes in it, namely BTNode and CompleteBinaryTree.

• The BTNode class is to represent the node of the binary tree. We inherit some properties of LLNode and we add a few new methods and properties to it.

• The CompleteBinaryTree class is to represent the whole tree, we will have a root instance variable and we will have methods to traverse the tree, know its size etc.

  

  BTNode Methods

• The getters and setters for left and right.

• Functions to overwrite the next variable from LLNode

• The printNode and value are inherited from LLNode

  

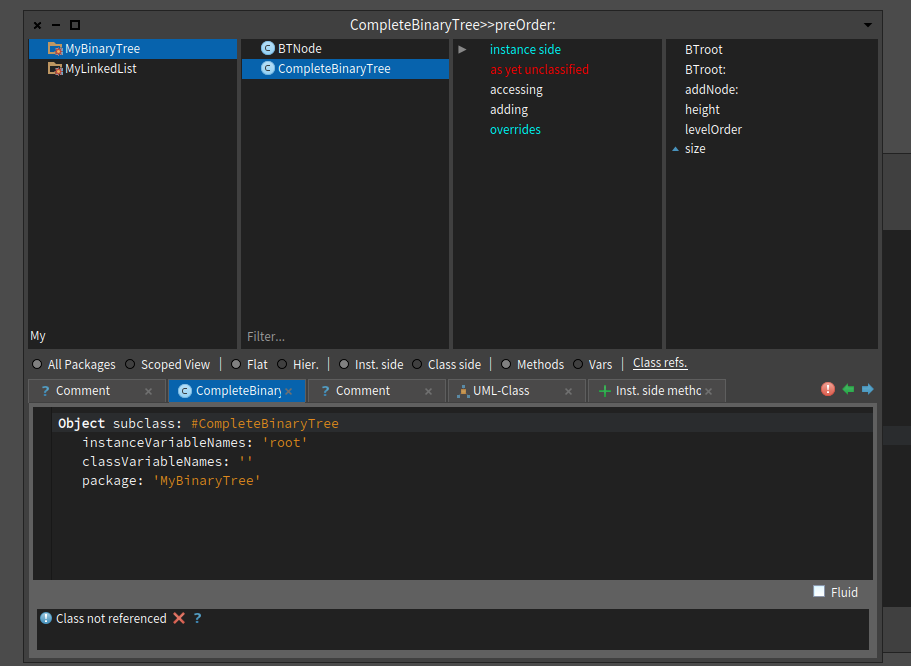
  CompleteBinaryTree Methods

• The getter and setter for the root variable.

• A method to get the height of a tree

• A method to level order traversal.

• A method to add a Node.

• A method to get the size(the total number of nodes)

Code

BTNode

Let's declare the class BTNode. We have seen that it needs to contain a

• value

• left pointer

• right pointer

But we know that value is already present as an instance variable in the LLNode class. So, we use inheritance and create BTNode as a subclass of the LLNode class.

LLNode subclass: #BTNode
    instanceVariableNames: 'left right'
    classVariableNames: ''
    package: 'MyBinaryTree'

But this comes with a problem, we don't want to use the next variable of the LLNode but it is inherited by default. To prevent the usage of next in BTNode we create a separate getter and setter for next saying that it is invalid.

next 

"This is written to overwrite the next functuion present in the superclass (LLNode) of BTNode"

    ^ 'Invalid method on BTNode'

next: aBTNode

"THis is written to overwrite the next: functuion present in the superclass (LLNode) of BTNode"

    ^ 'Invalid method on BTNode'

We also need to implement getter and setter Methods for left and right instance variables

BTNode>>left 
"returns the left BTnode"
    ^left

BTNode>>left: aBTNode

"sets the left BTnode in the tree"
    left:= aBTNode

BTNode>>right

"returns the right BTnode in the tree"
    ^right

BTNode>>right: aBTNode

"sets the right BTnode in the tree"
    right:= aBTNode

CompleteBinaryTree

Let's declare the class CompleteBinaryTree class. We declare root as the instance variable. Hence through this variable, we should be able to access the root of the tree.

Object subclass: #CompleteBinaryTree
    instanceVariableNames: 'root'
    classVariableNames: ''
    package: 'MyBinaryTree'

Getter and Setter

First, we need to define the getter and setter methods for root. Let's name the functions as BTroot and Btroot:

CompleteBinaryTree>>BTroot

"returns the value of root"
    ^root

CompleteBinaryTree>>BTroot: aBTNode

"sets the  root of tree"
    root := aBTNode

Height

Now let's right a function to find the height of the tree, since it is a CompleteBinaryTree, we just need to keep going to the left child node of the current Parent node until we reach nil. Since height is the distance of the farthest leaf from the root.

CompleteBinaryTree>>height 

"Since it is a complete binary tree , height is the farthest left leaf node"

    | node c|
    node := self BTroot .
    node ifNotNil: [ c:= 1 ] ifNil: [ c:=0 ].
    [ node left ]whileNotNil: [ c:=c+1 . 
                                node:= node left.].
    ^c

Level order traversal

Now to traverse the tree in a level-order fashion we follow a few steps:

• Check if the root node is nil. If so return, empty tree.

• If not, then add it to a queue (a simple OrderedCollection) and while the queue is not empty add the children of the first element of the queue.

• Return the collection.

The above-mentioned steps are exactly what is done in the code below.

CompleteBinaryTree>>levelOrder

"Traverse the tree in levelorder fashion from root "

|temp col q x|
col := OrderedCollection new.
q := OrderedCollection new.
temp := self BTroot .

temp ifNotNil: [ q add: temp  ]
          ifNil: [ ^'Empty tree' ].

[q isEmpty] whileFalse: [ temp left ifNotNil:[q add: temp left ].
                 temp right ifNotNil:[q add: temp right ].
                 x := q removeFirst.
                 col add:x value.
                q ifNotEmpty: [temp := q first.].       ].

^col

Size

The number of nodes of the tree would basically be the number of nodes traversed in the LevelOrder Traversal. So, we could just return the length of the collection we obtain the LevelOrder Method.

CompleteBinaryTree>>size 

"The total number of nodes --> the number of items in the levelOrder traversal "

    ^(self levelOrder size)

addNode: aBTNode

The addNode function takes an argument which is aBTNode i.e the node to be added to the tree.

CompleteBinaryTree>>addNode: aBTNode

"add an node in a complete binary tree "

|temp q|
q := OrderedCollection new.
temp := self BTroot .

temp ifNotNil: [ q add: temp  ]
          ifNil: [ ^'Empty tree' ].

[q isEmpty] whileFalse: [ 
        temp left ifNotNil:[q add: temp left ]
                       ifNil:[temp left: aBTNode. ^'Node added'. ].
        temp right ifNotNil:[q add: temp right ]
                    ifNil:[temp right:  aBTNode. ^'Node added'. ].
        q removeFirst.
        temp := q first.       ].

Here, we first check if the root is nil or not. Then we proceed to traverse the tree in a level order fashion and the moment we find a nil node, we add our node over there as in a complete binary tree nodes are supposed to be filled in the level order fashion.

There are more functions such as the inorder and the other traversals that can be added to this class. I will update the blog, once I implement them.

Protocols

Generally, the methods are by default grouped into protocols. But sometimes it doesn't happen and you might have the panes of the system browser looking like this:

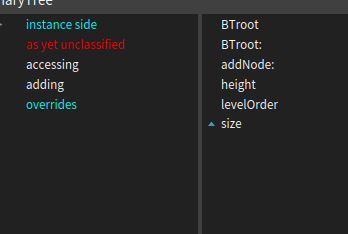
Some methods are already grouped. For eg: the addNode method has correctly been assigned the group of adding. Similarly, the other methods also need to be classified. So, we will manually classify the as yet unclassified methods, by clicking on them.

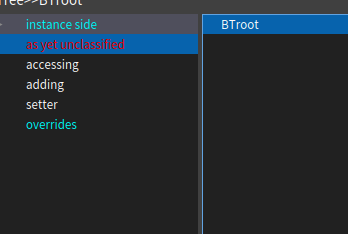
Suppose, we want to keep the BTroot in the accessing group, we right-click on BTroot and put in the respective group as shown in the image below.

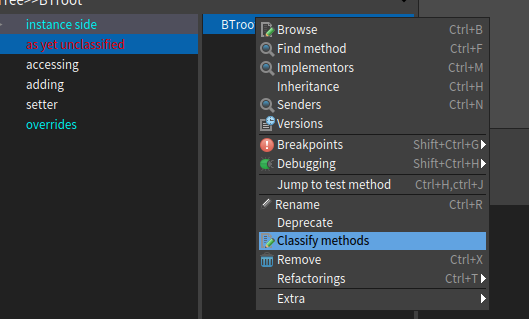
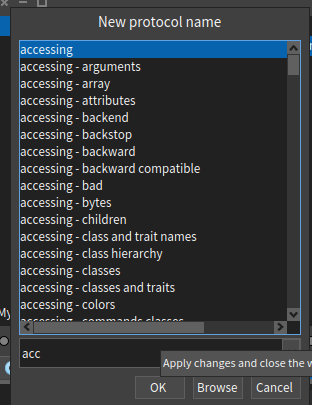
Then the methods get classified and finally the pane would look as shown below.

Testing

"A code that cannot be tested is flawed"

To get started create a new class that inherits the TestCase class:

TestCase subclass: #BTTest
    instanceVariableNames: ''
    classVariableNames: ''
    package: 'MyBinaryTree'

Okay, so we will be doing the 3 tests in this class.

1. Check whether the root value is set properly or not.

2. Whether the CompleteBinarytree is initialised properly or not.

3. Check whether levelOrder is working or not.

4. Check whether the node gets added to the right place in the tree or not.

Note that test names should start with the word 'test' .

Test 1

We create a BTnode and set it value to a particular value and then use assert equals to check if it works.

BTTest>>testRootValSetCheck

| root |

root := BTNode new.        
root value:3.
self assert: root value equals:3

If test goes right, then a message as shown below will pop up.

Similarly , let's implement Test 1 , Test 2 and Test 3

Test 2

BTTest>>testHeightCheck

|root n1 n2 n3 n4 n5 bintree|

root := BTNode new.
n1 := BTNode new.
n2 := BTNode new.
n3 := BTNode new.
n4 := BTNode new.
n5 := BTNode new.

root value: 1.
n1  value: 2.
n2  value: 3.
n3  value: 4.
n4  value: 5.
n5  value: 6.

root left: n1.
root right: n2.
n1 left: n3.
n1 right: n4.

bintree := CompleteBinaryTree new.
bintree BTroot:root.

self assert: bintree height equals:3

Test 3

BTTest>>testCheckLevelOrder

|root n1 n2 n3 n4 n5 bintree|

root := BTNode new.
n1 := BTNode new.
n2 := BTNode new.
n3 := BTNode new.
n4 := BTNode new.
n5 := BTNode new.

root value: 1.
n1  value: 2.
n2  value: 3.
n3  value: 4.
n4  value: 5.
n5  value: 6.

root left: n1.
root right: n2.
n1 left: n3.
n1 right: n4.

bintree := CompleteBinaryTree new.
bintree BTroot:root.

self assert: bintree levelOrder equals:#(1 2 3 4 5) asOrderedCollection.

Test 4

BTTest>>testCheckaddNode

|root n1 n2 n3 n4 n5 bintree|

root := BTNode new.
n1 := BTNode new.
n2 := BTNode new.
n3 := BTNode new.
n4 := BTNode new.
n5 := BTNode new.

root value: 1.
n1  value: 2.
n2  value: 3.
n3  value: 4.
n4  value: 5.
n5  value: 6.

root left: n1.
root right: n2.
n1 left: n3.
n1 right: n4.

bintree := CompleteBinaryTree new.
bintree BTroot:root.

bintree addNode: n5.

self assert: bintree levelOrder equals:#(1 2 3 4 5 6) asOrderedCollection.

Let's Test all of them together by pressing on the circle button infront of BTTest in the Browser pane

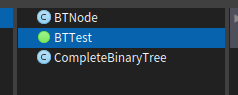
If you get a pop- up at the bottom right of your screen showing that All Tests are passed then 'Hurray!' . We are done with the basic implementation of a Complete Binary Tree . This could be further improved by adding new functions such as inOrder, preOrder and postOrder etc...

Thank you for reading the blog!!. Any suggestions , improvements , advice or constructive criticism will be taken as I am also a still learning!