Artificial Neural Networks -Part1: Introduction and Feedforward

Artificial neural networks (ANNs) are a type of machine learning algorithm that can learn from data and perform tasks such as classification, regression, clustering, anomaly detection, etc. ANNs are inspired by the structure and function of biological neural networks, which are composed of interconnected neurons that transmit signals to each other.

What is a neuron?

A neuron is a basic unit of information processing in the brain. It has three main components: dendrites, cell body (or soma), and axon. Dendrites receive inputs from other neurons or external sources. The cell body integrates these inputs and generates an output signal based on a threshold value. The axon carries the output signal to other neurons or target cells.

What is an artificial neuron?

An artificial neuron is a mathematical model that simulates the behavior of a biological neuron. It has three main components: inputs, weights, and activation function. Inputs are numerical values that represent features or attributes of data. Weights are parameters that determine how much each input contributes to the output. Activation function is a nonlinear function that maps the weighted sum of inputs to an output value.

What is an artificial neural network?

An artificial neural network is a collection of artificial neurons arranged in layers. Each layer has one or more neurons that receive inputs from previous layers or external sources and produce outputs for next layers or final results. There are different types of layers depending on their role and function in the network:

• Input layer: This layer receives raw data as inputs and passes them to the next layer without any modification.

• Hidden layer: This layer performs some computation on the inputs received from previous layers and produces outputs for next layers. There can be one or more hidden layers in an ANN depending on its complexity and depth.

• Output layer: This layer produces final outputs or predictions based on the inputs received from previous layers.

The connections between neurons in different layers have weights associated with them. These weights are learned by the network during training using various learning algorithms such as gradient descent, backpropagation, etc.

How does an artificial neural network work?

An artificial neural network works by propagating signals forward and backward through its layers until it reaches a desired level of accuracy or convergence. The forward propagation involves computing outputs for each layer based on inputs and weights using activation functions. The backward propagation involves updating weights for each connection based on errors between actual outputs and desired outputs using learning rules.

The process of forward propagation can be illustrated by the following example:

Suppose we have an ANN with one input layer (X), one hidden layer (H), and one output layer (Y). The input layer has two neurons (x1 and x2), the hidden layer has three neurons (h1, h2, h3), and the output layer has one neuron (y). The activation function used for all neurons is sigmoid, which is defined as:

sigmoid(x) = 1 / (1 + exp(-x))

The following figure shows the structure of this ANN:

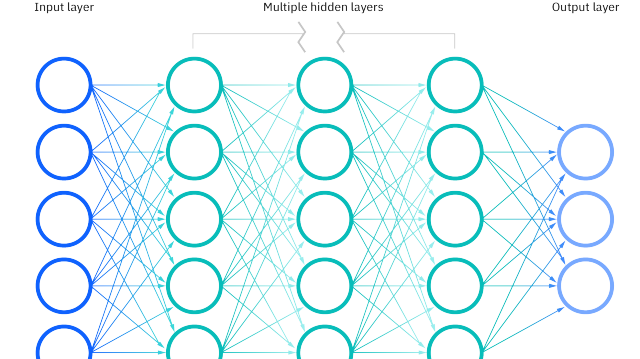
Now suppose we have an input vector [0.5, 0.8] that represents some data point we want to classify or predict using this ANN. To compute the output y for this input vector, we need to perform forward propagation as follows:

Step 1: Calculate weighted sum for each neuron in hidden layer

h1 = w11 x1 + w12 x2 + b1 h2 = w21 x1 + w22 x2 + b2 h3 = w31 x1 + w32 x2 + b3

where wij are weights for connections between input i and hidden j neurons, and bj are biases for hidden j neurons.

Step 2: Apply activation function to get outputs for each neuron in hidden layer

h1 = sigmoid(h1) h2 = sigmoid(h2) h3 = sigmoid(h3)

Step 3: Calculate weighted sum for output neuron

y = v1 h1 + v2 h2 + v3 * h3 + c

where vj are weights for connections between hidden j and output neurons, and c is bias for output neuron.

Step 4: Apply activation function to get final output

y = sigmoid(y)

This completes forward propagation for this ANN with given input vector [0.5, 0.8]. The final output y represents the prediction or classification made by this ANN for this input vector.