Summarising Numerical Data - Mean
 Pyari Kumaran
Pyari KumaranMean is the most commonly used measure of central tendency. Mean is also called average. It is relied on as a measure of central tendency when there are no outliers. In this post, we will see how to calculate the mean of a given dataset depending on the kind of data we have.
Case 1: A series of discrete data
[2,1,3,4,5,2,3,3,3,4,4,1,2,3,4]
If the data is in the form above, the mean can be calculated using the formula
$$\bar{x}=\frac{(x_1+x_2+...+x_n)}{n}.$$
where n is the number of items in the data set
ie, the mean in the above case will be:
$$\bar{x} =\frac{(2+1+3+4+5+2+3+3+3+4+4+1+2+3+4)}{15}$$
$$ie, \bar{x} = 2.9333$$
Case 2: When we have grouped data with discrete elements as in the below case.
| Value | Frequency |
| 1 | 2 |
| 2 | 3 |
| 3 | 5 |
| 4 | 4 |
| 5 | 1 |
We calculate the average in the case of grouped data using the formula:
$$\bar{x} = \dfrac{\sum_{i=1}^{n}f_ix_i }{\sum_{i=1}^{n}f_i}$$
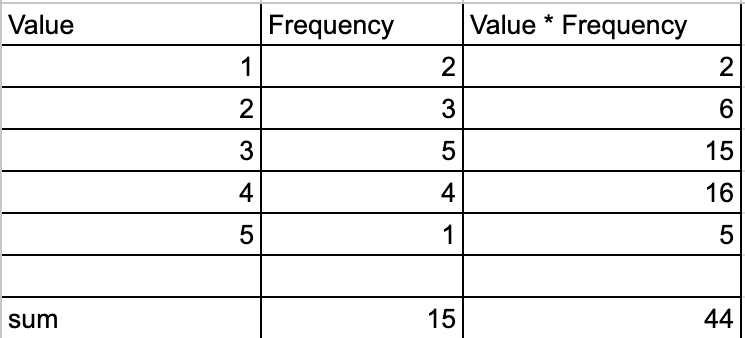
From the above calculation, we get
$$\sum_{i=1}^{n}f_ix_i = 44\: and \: \sum_{i=1}^{n}f_i = 15$$
$$Therefore,\, the \, mean \,in \,the\, above\, case\, is\, \frac{44}{15} = 2.9333$$
Note that, the mean is the same as in case 1.
Case 3: Mean in the case of grouped continuous data as intervals as in the below example.
The mean is calculated using the formula:
$$\bar{x} = \frac{\sum_{i=1}^{n}f_im_i}{\sum_{i=1}^{n}f_i}$$
In the above formula, m is the midpoint of the interval and f is the frequency of the data in that interval
| Class Interval | Frequency (f_i) | mid-point of interval (m_i) | f_i*m_i |
| 30-40 | 3 | 35 | 105 |
| 40-50 | 6 | 45 | 270 |
| 50-60 | 18 | 55 | 990 |
| 60-70 | 17 | 65 | 1105 |
| 70-80 | 4 | 75 | 300 |
| 80-90 | 2 | 85 | 170 |
Some notes on mean:
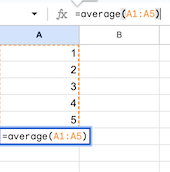
- Mean of a column of values in a spreadsheet can be calculated using the formula average
- If all the values in a data set is increased by a fixed constant c, the mean of the data set will also get added by the same constant c
Subscribe to my newsletter
Read articles from Pyari Kumaran directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
