preorder = root left right
DFS use stack = inorder= left root right
postorder = left right root
BFS use queue = print each level

Graph

• Used to represent various real-world scenarios such as social networks, transportation systems, and computer networks.

• A collection of nodes or vertices connected by edges.

• Edges represent relationships or connections between nodes.

• Edges can be directed or undirected.

• Cycles (paths with the same starting and ending points) may be present.

Graph Terminology

• Node: A single vertex in a graph or tree. Nodes can contain data or objects and are connected to other nodes through edges.

• Edge: A line representing a connection between nodes in a graph or tree. Edges can be directed or undirected.

• Depth: The length of the path from a node to the root node. The depth of a specific node is the number of edges connecting it to the root node. In a tree, the root node has a depth of 0, and the depth increases by 1 for each subsequent level.

• Breadth: Although not typically used in the context of trees, breadth is a term used in breadth-first search (BFS). Nodes at the same level (depth) in the tree are visited "all at once" in BFS, which is why the term "breadth" is used. Therefore, in BFS, "breadth" refers to the level (depth) of a node in the tree, not the order of traversal.

Example

Traversal Methods

Graph traversal is generally tailored to recursive functions.

DFS Depth-First Search

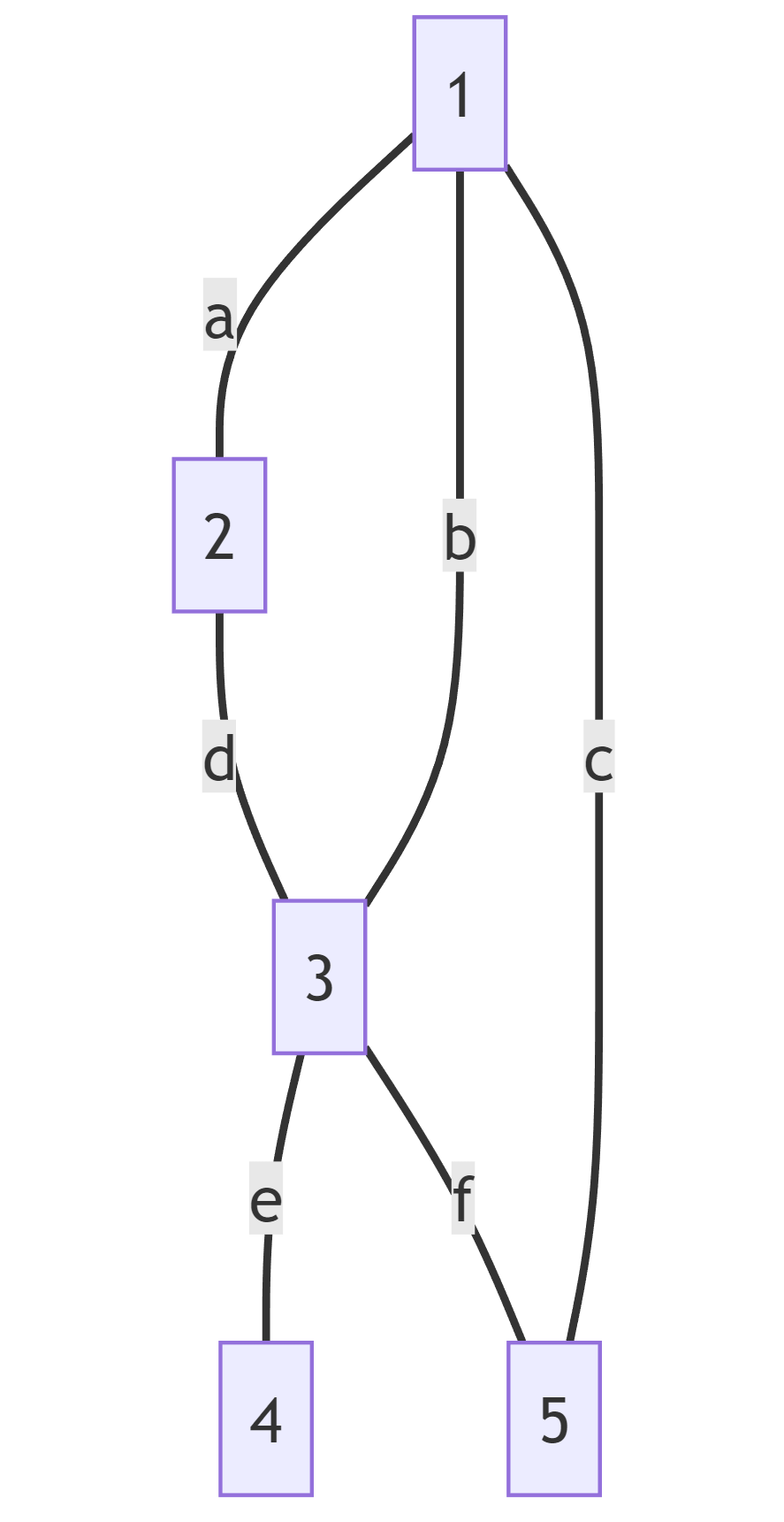
• Push the starting node 1 into the stack.

• The stack currently contains [1].

• Pop node 1 from the stack and print it.

• The stack currently contains [].

• Following edges a, b, and c connected to node 1, push nodes 2, 3, and 5 into the stack.

• The stack currently contains [5, 3, 2].

• Pop node 2 from the stack and print it.

• The stack currently contains [5, 3].

• Following edge d connected to node 2, push node 3 into the stack.

• The stack currently contains [5, 3, 3].

• Pop node 3 from the stack and print it.

• The stack currently contains [5, 3].

• Following edges e and f connected to node 3, push nodes 4 and 5 into the stack.

• The stack currently contains [5, 4, 5].

• Pop node 5 from the stack and print it.

• The stack currently contains [4].

• Following edge g connected to node 5, push node 4 into the stack.

• The stack currently contains [4, 4].

• Pop node 4 from the stack and print it.

• The stack currently contains [].

• As there are no more nodes to pop from the stack, the DFS traversal ends.

BFS (Breadth-First Search)

• Insert the starting node 1 into the queue.

• The queue now contains [1].

• Remove node 1 from the queue and print it.

• The queue now contains [].

• Traverse the edges a, b, and c connected to node 1 and insert nodes 2, 3, and 5 into the queue, respectively.

• The queue now contains [2, 3, 5].

• Remove node 2 from the queue and print it.

• The queue now contains [3, 5].

• Traverse the edge d connected to node 2 and insert node 3 into the queue.

• The queue now contains [3, 5, 3].

• Remove node 3 from the queue and print it.

• The queue now contains [5, 3].

• Traverse the edges e and f connected to node 3 and insert nodes 4 and 5 into the queue, respectively.

• The queue now contains [5, 3, 4, 5].

• Remove node 5 from the queue and print it.

• The queue now contains [3, 4, 5].

• Traverse the edge g connected to node 5 and insert node 4 into the queue.

• The queue now contains [3, 4, 3].

• Remove node 3 from the queue and print it.

• The queue now contains [4, 3].

• Node 5 connected to node 3 has already been inserted into the queue, so it is ignored.

• Remove node 4 from the queue and print it.

• The queue now contains [3].

• Remove node 3 from the queue and print it.

• The queue now contains [].

• Since there are no more nodes to be removed from the queue, the BFS search is complete.

Tree

• Used to represent hierarchical structures such as file systems, organization charts, and family trees.

• A type of graph.

• There is only one path between any two nodes.

• There are no cycles (paths that start and end at the same node).

Tree Terminology

• Branch: An edge that connects a node in a tree to a root or another node. There can be multiple branches between a root and another node.

• Root: The topmost node in a tree. Every other node is either a branch starting from the root or a leaf node.

• Leaf: The final node in a tree that has no children. It is the last node that does not extend to any other node.

• Parent: A node in a tree that has one or more child nodes. It is the node located above the current node when following the edges of the tree towards the root.

• Child: A node in a tree that has a parent node. It is the node located below the current node when following the edges of the tree towards the leaves.

Example

Tree Traversal Methods

Preorder (Preorder Traversal)

Preorder traversal is a method where the root node is visited first. That is, after printing the root node, traverse the left subtree, and then the right subtree. Preorder traversal visits nodes in the following order:

1. Root node

2. Left subtree

3. Right subtree

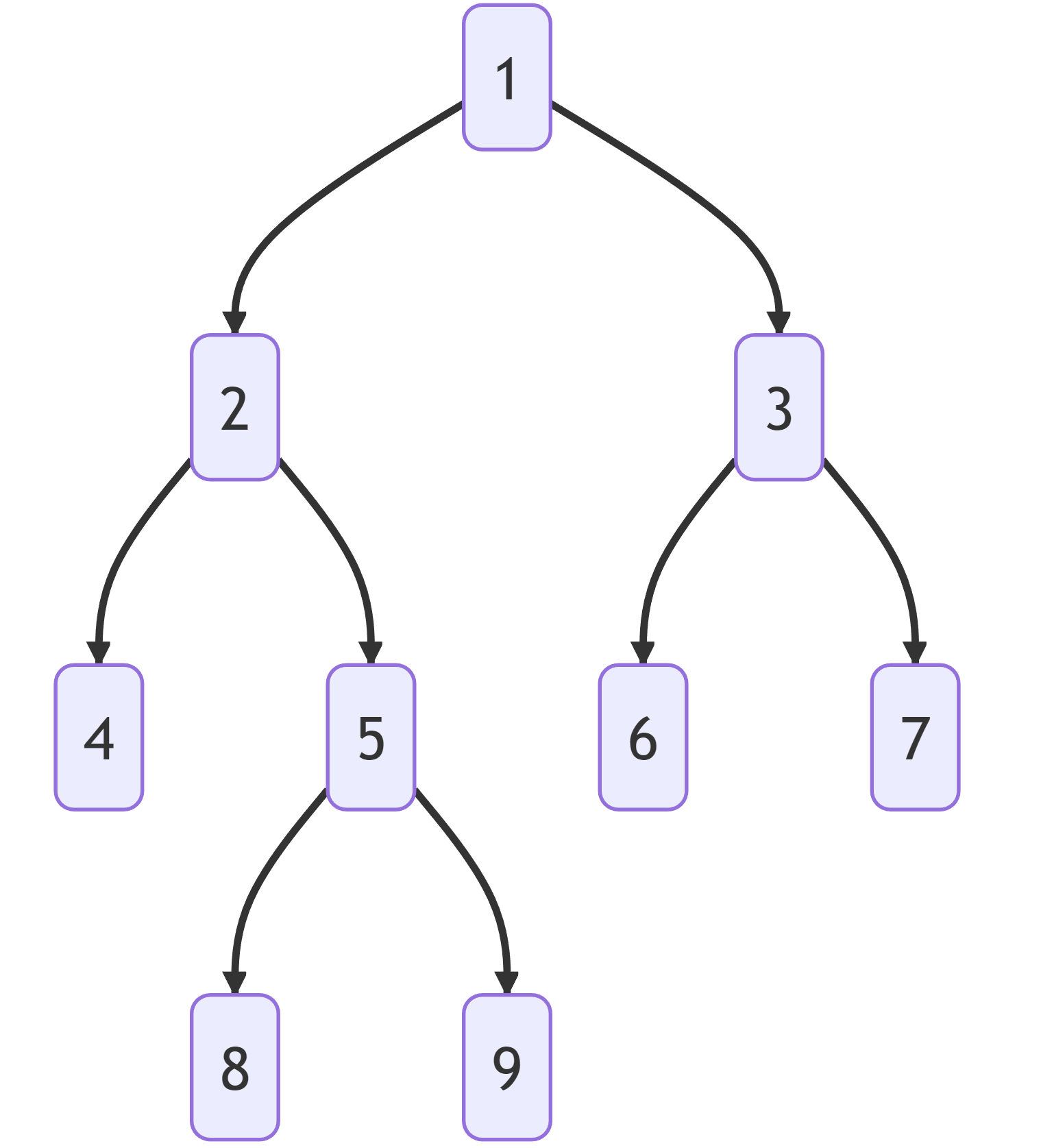
• Example: Preorder: 1 2 4 5 8 9 3 6 7

Inorder (Inorder Traversal)

Inorder traversal is a method where the root node is visited in the middle. That is, after traversing the left subtree, print the root node, and then traverse the right subtree. Inorder traversal visits nodes in the following order:

1. Left subtree

2. Root node

3. Right subtree

• Example: Inorder: 4 2 8 5 9 1 6 3 7

Postorder (Postorder Traversal)

Postorder traversal is a method where the root node is visited last. That is, after traversing the left subtree and the right subtree, print the root node. Postorder traversal visits nodes in the following order:

1. Left subtree

2. Right subtree

3. Root node

• Example: Postorder: 4 8 9 5 2 6 7 3 1

Understanding these traversal methods is essential for solving various tree-related problems in computer science. Each traversal method has its unique use-cases and can be applied according to the requirements of a specific problem.