Probability For Mastering Data Science - Part 2

In the previous part, we covered Combinatorics today we gonna continue with Sets and Events.

Sets and events👇

We use the upper-case letter to denote sets and we use the lower-case letter to denote individual elements.

The empty set is denoted by ∅.

• “X ∈ A” means x is an element of the set A.

• ∀ = for all/any.

• “∀x ∈ A = for all in x in A”

• “:” = such that

What is Subset?👇

A subset is a set that is fully contained in another set.

For example -

Every element of A is also an element of B = A is a subset of B or (A ⊆ B).

Every set contains at least 2 sets. For example-

A ⊆ A and Ø ⊆ A.

Ways sets can interact👇

1. Multiple events:

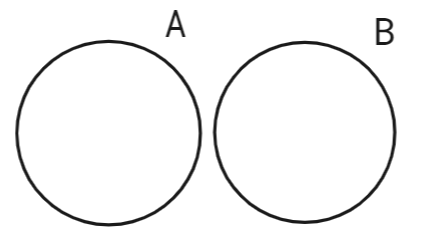
If the circle of events A and B never touch, then the two events can never happen simultaneously. Essentially, event A occurring guarantees that event B not occurring.

1. Intersecting:

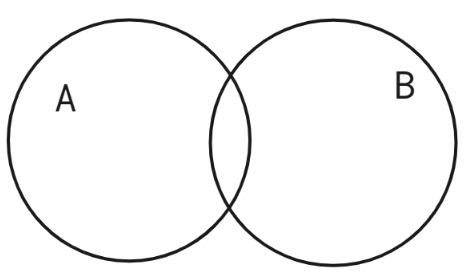
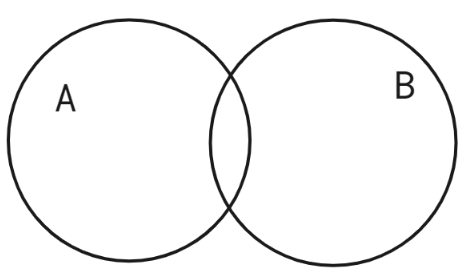
If the circle intersects, it means that the two events can occur at the same time.

1. Subset:

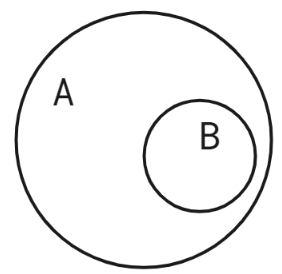
In that case, one event can only ever occur if the other one does as well.

If an outcome is not part of a set, it can’t be part of any of its subsets.

An outcome not being part of some subset does not exclude it from the entirety of the greater set.

Intersection of sets👇

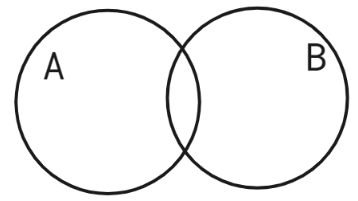
Intersection → A ∩ B.

We use intersections to denote instances where both events A and B happen simultaneously.

Union of sets👇

What is a Union of Sets?👇

The union of two sets is a combination of all outcomes preferred for either A or B.

We denote the union of two sets. For example -

A ∪ B

If sets A and B don’t touch at all, their union would simply be their sum. For example -

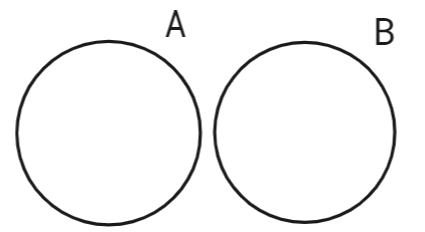
\=> A ∩ B = ∅

\=> A ∪ B = A + B

If the event intersect, then-

If the event is overlapping, then-

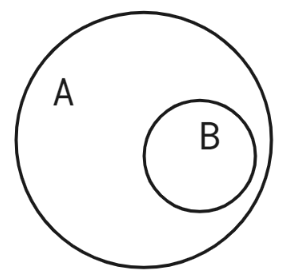
\=> A ∪ B = A

\=> A ∩ B = B

Mutually exclusive sets👇

What are Mutually exclusive sets?👇

Mutually exclusive sets are sets that are not allowed to have overlapping elements.

The intersection of a mutually exclusive set is an empty set. This means the intersection of any number of sets is the empty set, then they must be mutually exclusive.

If sets are mutually exclusive then their union should be their sum. For example-

A ∪ B = A + B

Sets have compliments too.

Compliment set: All values that are part of the sample space, but not part of the set.

Compliments are always mutually exclusive.

Not all mutually exclusive sets are a compliment.

Independent and dependent events👇

The probability of an event changes depending on the information we have.

If two events A and B, then the probability of getting a, if we are given that B has occurred then we denote that following-

P(A|B) —> “A given B”

Where,

P(A|B) is called conditional probability

We use it to distinguish dependent from independent events.

Conditional Probabilities👇

What are Conditional probabilities?👇

Conditional probabilities is the likelihood of an event occurring, assuming a different one has already happened.

Formula-

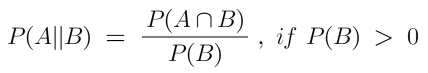
For Example-

In that case,

E = Economics

H = Honours

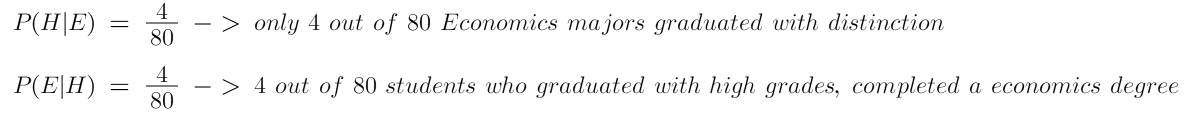
The law of total probability👇

If,

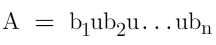
Then,

The probability of A,

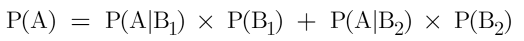
For example-

	Veg.	Non-veg.	Total
Male	15	32	47
Female	29	24	53
Total	44	56	100

The additive rule👇

The probability of the union of two sets is equal to the sum of the individual probabilities of each event minus the probability of their intersection. For example-

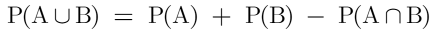
	Veg.	Non-veg.	Total
Male	15	32	47
Female	29	24	53
Total	44	56	100

So that means there is a 76% chance that a random person from the survey is either Male Veg or both.

The Multiplication rule👇

The formula for the multiplication rule-

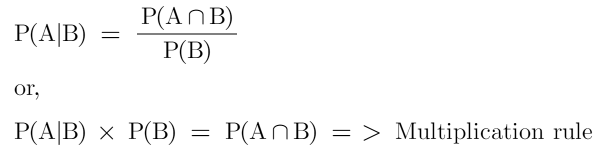
For example-

P(B) = 0.5

P(A|B) = 0.8

So,

P(A ∩ B) = P(A|B) × P(B) = 0.8 × 0.5 = 0.4

Baye’s law👇

Baye’s law helps us to find a relationship between the different conditional probabilities of two events.

We know that,

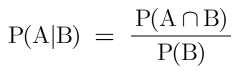
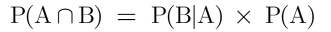
Then,

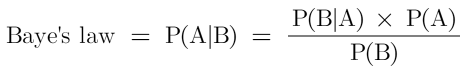
For example-

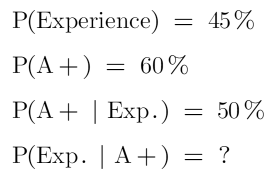
Note: Baye’s rule doesn’t work on independent events.

Before we end…

Thank you for taking the time to read my posts and share your thoughts. If you like my blog please give a like, comment and share it with your circle and follow for more, I look forward to continuing this journey with you.

Let’s connect and grow together.I look forward to getting to know you better.

Here are my social links below-

Linkedin: https://www.linkedin.com/in/ai-naymul/

Twitter: https://twitter.com/ai_naymul

Github: https://github.com/ai-naymul