Quick sort is a widely used sorting algorithm that follows the divide-and-conquer strategy. It selects a pivot element, partitions the array around the pivot, and recursively sorts the subarrays, resulting in an efficient and in-place sorting method.
In general, when we talk about sorting, it means we talk about arranging elements in increasing order.

Method

First of all, The Requirement is the choice of the pivot point.

We can choose any element as a pivot element like,

First element
Middle element
Last element
or maybe any random element

This pivot point is required in this algorithm because recursively, the array will sort about this point only.

Implementation of Quick Sort program

Create a recursive function, say quicksort(), this recursion function will call the partition() function recursively until the array has not been sorted.
This function will again call the quicksort() function to sort the left half array and right half array until the left pointer does not exceed the right pointer.
These low and high pointers signify the range of the array required to be sorted.
On every call, first of all, it will check that the low should be less than the high pointer.
Now, let's talk about the partition, This partition is done about the pivot point as mentioned earlier. Then, two recursion calls are takes place after partition, one for the left part and another for the right part about the pivot point.
It means, first in the stack left most of the array will sort first, then on returning to the right part of the array the pivot point will go for sort.
Hence, on the wrap of the recursion calls, sorting will be done.

Implementation of the Partition program

The partition function will take, a full array, say arr, lowest point, saylow, and highest point, say high as the input.
This array will take by reference as input as sorting is directly done by the input array.
Inside the program of partition(), it is required to choose a pivot point according to your convenience, here right-most points will be considered as the pivot point.
After choosing the pivot point, let's start from the leftmost element and keep track of the index of the smaller or equal elements, here say low-1, about the pivot point and swapping the current element, here say arr[j], with the smaller element. Otherwise, ignore the swapping operation and move to the next indexed element.
At the end swap the last smaller element, say arr[i + 1] with the highest element, say arr[high] and return the index of the smaller element, here i+1.

Code

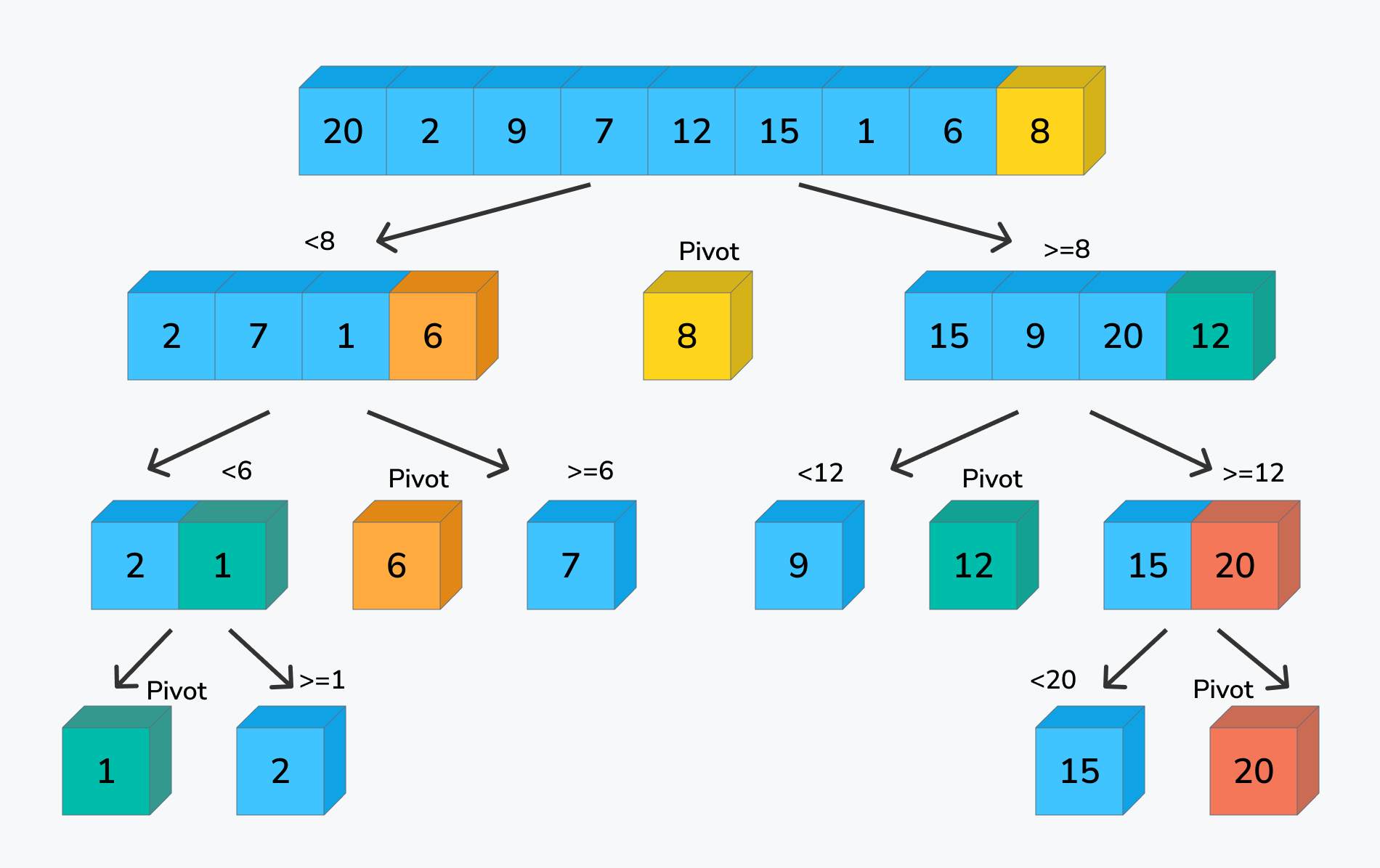
Example

C++

#include <bits/stdc++.h>
using namespace std;
int makePartition(vector<int>& arr, int low, int high) {
    int pivot = arr[high];
    int i = (low - 1);
    for (int j = low; j <= high - 1; j++) {
        if (arr[j] < pivot) {
            i++;
            swap(arr[i], arr[j]);
        }
    }
    swap(arr[i + 1], arr[high]);
    return (i + 1);
}

void quickSort(vector<int>& arr, int low, int high) {
    if (low < high) {
        int pi = makePartition(arr, low, high);
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

int main() {
    vector<int> arr = {20, 2, 9, 7, 12, 15, 1, 6, 8};
    int n = arr.size();
    quickSort(arr, 0, n - 1); // Sorting is done recursiverly
    cout << "Sorted array: " << endl;
    for (int i = 0; i < N; i++)
        cout << arr[i] << " ";
    cout << endl;
    return 0;
}

Python

def makePartition(arr, low, high):
    pivot = arr[high]
    i = low - 1
    for j in range(low, high):
        if arr[j] <= pivot:
            i = i + 1
            (arr[i], arr[j]) = (arr[j], arr[i])
    (arr[i + 1], arr[high]) = (arr[high], arr[i + 1])
    return i + 1

def quicksort(arr, low, high):
    if low < high:
        pi = makePartition(arr, low, high)
        quicksort(arr, low, pi - 1)
        quicksort(arr, pi + 1, high)

if __name__ == '__main__':
    arr = [20, 2, 9, 7, 12, 15, 1, 6, 8]
    n = len(arr)
    quicksort(arr, 0, n - 1)
    print('Sorted array:')
    for x in arr:
        print(x, end=" ")
    print("\n")

Complexity Analysis

Time Complexity:

Best Case: O( n log(n) )
Average Case: O( n log(n) )
Worst Case: O( n^2 )

Space Complexity:

O ( n ) // This is due to recursion calls in the stack

Precautions while selecting the pivot point

Randomization: This will remove the chances of the worst-case scenarios.
Median of Three: Instead of choosing the last element as a pivot point, It is advisable to take the median of the first, middle, and last element of the array as the pivot point of the array. This will reduce the risk of choosing extreme values.
Avoiding sorted and nearly sorted arrays: Quick sort algorithm will degrade the program's efficiency.
Select the pivot point in such a way as to handle the duplicate values in the arrays. Techniques like the "Dutch National Flag" algorithm or "Hoare's Partition Scheme" can be employed to handle duplicate values more efficiently.

Quick Sort Algorithm

Table of contents