Learning rate

As rice is the essential ingredient for cooking fried rice, the learning rate is the fundamental element that brings meaning to machine learning and deep learning. It plays a crucial role in the models we build, enabling them to learn and improve over time, producing accurate and reliable results. The learning rate, intricately connected with the loss function, guides the optimization process, determining how quickly or gradually the model adapts and converges toward optimal performance. Without carefully tuning the learning rate as a hyperparameter, the model's ability to learn and produce desirable outcomes would be greatly hindered. So, just like rice completes a delicious fried rice dish, the learning rate empowers our models to achieve remarkable learning and deliver impactful results in the world of machine learning.

The Learning Rate is a vital hyperparameter deeply integrated into the optimization algorithm, playing a significant role in enhancing its performance when appropriately tuned. It acts as a multiplier for the resulting gradient descent during training, effectively minimizing the loss. In simpler terms, the learning rate can be seen as the step size we take in each iteration of the optimization process. By carefully adjusting this value, we can navigate the optimization landscape more efficiently, achieving faster convergence and ultimately improving the model's overall performance.

In the pursuit of finding the optimal learning rate, striking the right balance is important. If the learning rate is set too high, we run the risk of overshooting and taking excessively large steps toward minimizing the loss. On the other hand, a lower learning rate necessitates numerous updates before reaching the minimum point, as smaller steps are taken to gradually reduce the loss. Therefore, our aim is to target the optimal learning rate, one that is neither too high nor too small. By finding this sweet spot, we can ensure efficient convergence towards the minimum loss, striking a harmonious balance between rapid progress and steady refinement.

Behind The Scene Of How The Learning Rate Drives Loss Minimization

During the training phase of a machine learning model, the goal is to find the optimal values for the model's weights (w). The weights determine the influence of each input feature on the model's predictions. The process of updating the weights involves minimizing the loss function (J(w,b)), which measures the discrepancy between the model's predictions and the actual target values.

To update the weights, we first need to calculate the gradient of the loss function with respect to the weights. The gradient provides information about the direction and magnitude of the steepest ascent or descent in the loss function. It tells us how much each weight should be adjusted to minimize the loss. In summary, it is the derivative of the cost function (J(w,b)), given by

$$\frac{{\partial J(\mathbf{w},b)}}{{\partial w_j}} = \frac{1}{m} \sum_{i=0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})x_j^{(i)}$$

$$\frac{{\partial J(\mathbf{w},b)}}{{\partial b}} = \frac{1}{m} \sum_{i=0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})$$

where:

𝑚 is the number of training examples in the data set,
f_𝐰,𝑏(𝐱^(𝑖)) is the model's prediction, while 𝑦^(𝑖) is the target value.

The learning rate, denoted as (\alpha), is a hyperparameter that determines the step size for weight updates. It is then multiplied by the gradient, resulting in a scaled version of the gradient. This scaled gradient indicates the amount by which each weight should be adjusted:

$$\alpha \frac{{\partial J(\mathbf{w},b)}}{{\partial w_j}},\ \alpha \frac{{\partial J(\mathbf{w},b)}}{{\partial b}} \quad \text{for } j = 0..n-1$$

Next, the scaled gradient is subtracted from the current value of each weight. This subtraction step moves the weights in a direction that minimizes the loss. By iteratively updating the weights using this process, the model gradually learns to make better predictions:

The weight update equations are as follows:

𝑤𝑗 := 𝑤𝑗 - α(∂J(𝐰,𝑏)/∂𝑤𝑗) for 𝑗 = 0..𝑛−1 𝑏 := 𝑏 - α(∂J(𝐰,𝑏)/∂𝑏)

Here, 𝑛 is the number of features and the parameters 𝑤𝑗 and 𝑏 are updated simultaneously.

The iterations continue until the loss is minimized or reaches a satisfactory level. The number of iterations depends on factors such as the complexity of the problem, the size of the dataset, and the chosen learning rate. It is essential to strike a balance with the learning rate.

How to Choose The Optimal Learning Rate

The optimal learning rate also referred to as the descent learning rate serves a dual purpose as demonstrated below.

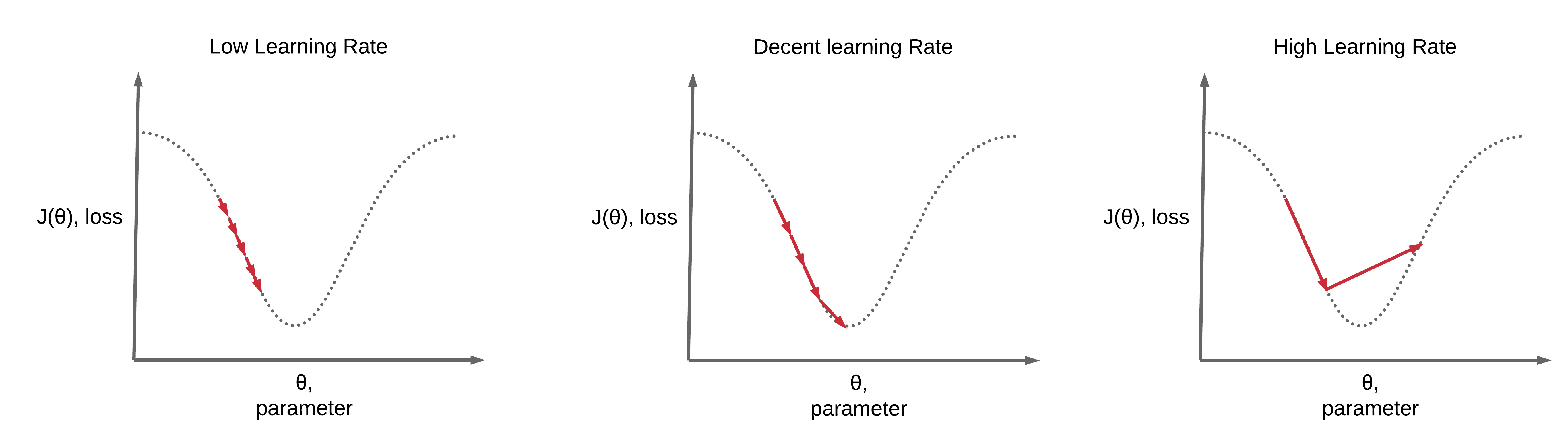
The objective is to select an optimal learning rate that best suits a specific problem. Here are two methods to determine the most suitable learning rate:

Grid Search

Learning rate Schedules

Grid Search

This is one of the techniques used to determine the optimal learning rate for a machine learning model, it involves manually setting a range of learning rates and allowing the model to select the best learning rate within that range. The range of learning rates is defined from a lower value to a higher value, covering a wide spectrum of possible learning rates. During this process, the model is trained and evaluated multiple times, with each iteration using a different learning rate from the predefined range. The model's performance metrics( accuracy or loss) are recorded for each learning rate. After exploring various learning rates, grid search helps identify the learning rate that yields the best performance on a validation set, which is the learning rate with the highest accuracy or lowest loss.

Implementation With Pytorch

The learning rate is passed through the optimizer during training so we need to import the necessary libraries.

import torch
import torch.optim as optim

The next step is to define the range of learning rates and iterate over them to find the optimal value. While the most commonly used range for learning rates falls between 0.001 and 0.1, it's important to note that you can customize this range to suit the requirements of your specific problem. It is recommended to experiment with different ranges to find the learning rate that yields the best performance and convergence for your model.

learning_rates = [0.001, 0.01, 0.1]
for lr in learning_rates:
    # Define your model, optimizer, and loss function
    model = YourModel()
    optimizer = optim.SGD(model.parameters(), lr=lr)
    loss_function = torch.nn.MSELoss()

Build the training loop

for epoch in range(num_epochs):
        # Perform forward pass, compute loss, and backpropagation
        outputs = model(inputs)
        loss = loss_function(outputs, labels)
        loss.backward()
        optimizer.zero_grad()
        optimizer.step()
        loss.backward()

Evaluate the model performance

# Evaluate the model's performance on the validation set
    with torch.no_grad():
        val_outputs = model(val_inputs)
        val_loss = loss_function(val_outputs, val_labels)
        accuracy = compute_accuracy(val_outputs, val_labels)

View what is happening by printing the result of each learning rate

print(f"Learning Rate: {lr}, Validation Loss: {val_loss}, Accuracy: {accuracy}")

Select the best learning rate based on the validation results and retrain the model

best_lr = choose_best_learning_rate()  
model = YourModel()
optimizer = optim.SGD(model.parameters(), lr=best_lr)
loss_function= torch.nn.MSELoss()

Then train the model with the selected learning rate on the whole training dataset.

Grid search saves us from the trial-and-error process of manually selecting a single learning rate and also helps us efficiently explore and select the most suitable learning rate, enabling models to achieve better performance and convergence during training. However, it can be computationally expensive, requiring multiple model training and evaluations for each combination of hyperparameters. This leads to increased time and resource requirements. In addition, the performance of grid search is highly dependent on the granularity of the grid, which may result in missed optimal values. To overcome these limitations, we can consider other methods provided.

Learning Rate Schedules

Learning rate schedules are techniques used to find the optimal learning rate for a machine learning model, the process is also called learning rate decay. It involves initially setting a higher learning rate and then gradually reducing it to the optimal value using a learning rate scheduler. The purpose of Learning rate schedules is to enable faster initial learning by allowing the model to make larger parameter updates. As training progresses, the learning rate is systematically decreased, leading to more refined and precise updates that help the model converge toward the optimal solution.

Different schedulers have their own characteristics and can be chosen based on the specific problem, model architecture, and dataset. The torch.optim.lr_scheduler package in PyTorch provides various learning rate schedulers including:

StepLR: This scheduler reduces the learning rate by a specified factor after a fixed number of epochs. The learning rate is multiplied by the gamma factor at each step.
MultiStepLR: Similar to StepLR, but allows for multiple step milestones at which the learning rate is reduced.
ExponentialLR: This scheduler applies an exponential decay to the learning rate at each epoch. The learning rate is multiplied by a decay factor, typically less than 1, to gradually decrease its value.
ReduceLROnPlateau: This scheduler monitors a specific metric, such as validation loss, and reduces the learning rate if the metric does not improve for a certain number of epochs. It helps fine-tune the learning rate during training.
CyclicLR: This scheduler cyclically varies the learning rate between a minimum and maximum value. It allows the learning rate to oscillate, which can help escape local minima and explore different regions of the solution space.
CosineAnnealingLR: This scheduler gradually reduces the learning rate following a cosine annealing schedule. It starts with a higher learning rate and decreases it in a smooth manner, resembling a cosine curve.
OneCycleLR: This scheduler combines the concepts of cyclical learning rates and learning rate annealing. It rapidly increases the learning rate, reaches a maximum, and then gradually decreases it towards the end of training.
LambdaLR is used to set the learning rate for each of the parameter groups. The function computes the multiplicative factor for each iteration according to the optimizer mentioned in the function and epoch ratios mentioned.
MultiplicativeLR is used to multiply the learning rate of each of the model parameters and group them accordingly by the factor given in the scheduler function.
ConstantLR is used to decay the learning rate factor gradually based on the model parameters through a constant until the model parameters iterate until the total iterations are passed by the model parameters.
LinearLR is used to decay the learning rate of each of the parameters based on linearly changing model parameters and the scheduler will iterate until the maximum iterations are reached by the model parameters.
ExponentialLR is used to decay the learning rate exponentially and the scheduler will iterate until the maximum model parameters are reached.

These schedulers have their own characteristics and can be explored for use. In this article, we will focus on the implementation of the StepLR scheduler. The StepLR scheduler adjusts the learning rate by a specified factor after a certain number of epochs. This can be useful for controlling the learning rate schedule and allowing it to adapt to the training progress. Let's delve into the details of implementing the StepLR scheduler in PyTorch.

Implementation With Pytorch

The learning rate is passed through the optimizer during training so we need to import the necessary libraries. we define a learning rate schedule using the StepLR scheduler from torch.optim.lr_scheduler module.

import torch
import torch.optim as optim
from torch.optim.lr_scheduler import StepLR

Specify the model and the loss function

model = YourModel()
loss_function = torch.nn.MSELoss()

We need to set the maximum learning rate and choose an optimizer. The maximum learning rate represents the upper bound of the learning rate range. It is important to select an appropriate value that suits your specific problem and model architecture. The optimizer is responsible for updating the model's parameters during training. PyTorch provides various optimizers, such as Stochastic Gradient Descent (SGD), Adam, and RMSprop, each with its own advantages and characteristics. The choice of optimizer depends on factors such as the nature of the problem and the properties of the dataset.

learning_rate = 0.1
optimizer = optim.SGD(model.parameters(), lr=learning_rate)

Define the learning rate schedule, step_size determines the number of epochs after which the learning rate is reduced, and gamma specifies the factor by which the learning rate is multiplied.

step_size = 10
gamma = 0.1
scheduler = StepLR(optimizer, step_size=step_size, gamma=gamma)

Build the training loop and Update the learning rate

for epoch in range(num_epochs):
        # Perform forward pass, compute loss, and backpropagation
        outputs = model(inputs)
        loss = loss_function(outputs, labels)
        loss.backward()
        optimizer.zero_grad()
        optimizer.step()
        loss.backward()
        scheduler.step()

Print the current learning rate Inside the training loop, after performing the forward pass, backward pass, and updating the parameters, we call scheduler.step() to update the learning rate according to the defined schedule and retrieve the current learning rate.

print(f"Learning Rate: {scheduler.get_last_lr()[0]}")

Learning rate schedulers, while useful, have some drawbacks. Firstly, they require manual selection and tuning of hyperparameters, making them a non-trivial task. Additionally, their effectiveness is problem-dependent, and what works for one problem may not work for another. The predefined patterns of some schedulers may not match the optimal learning rate changes needed by the model. Furthermore, implementing a scheduler adds computational overhead and can increase training time. It's crucial to evaluate and experiment with schedulers to understand their trade-offs and limitations, ensuring they provide benefits in a specific problem set.

Conclusively, selecting an appropriate learning rate plays a critical role in achieving optimal model training. Moving beyond trial and error, adopting a strategic approach that involves exploring learning rate techniques such as grid search, learning rate schedules, and adaptive methods can greatly enhance the training process. By carefully considering the characteristics, advantages, and disadvantages of these approaches, one can make informed decisions to improve model performance and convergence. Remember, the learning rate is a key factor in unlocking the full potential of your machine learning models, so choose wisely and iterate towards excellence. Happy training!

If you have any further questions or need clarification, please feel free to reach out to me on LinkedIn. Thank you for taking the time to read the article.

References

Image credit

PyTorch Learning Rate Scheduler Official Documentation

Gradient Descent In Practice By Andrew Ng

Beyond Trial and Error: A Strategic Approach to Choosing Learning Rate for Improved Model Training.

Table of contents

Behind The Scene Of How The Learning Rate Drives Loss Minimization

How to Choose The Optimal Learning Rate

Grid Search

Learning Rate Schedules

References

Subscribe to my newsletter

Fatimo Adebanjo

Fatimo Adebanjo