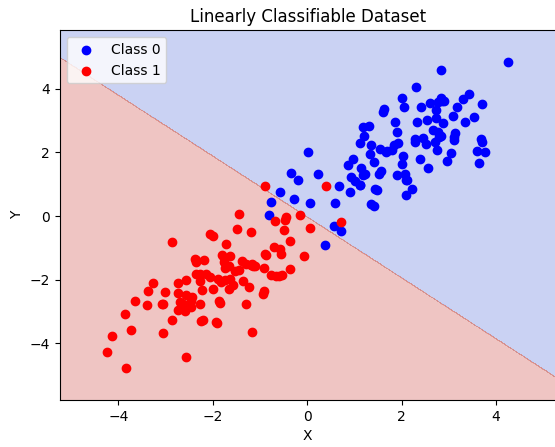
Linearly Classifiable Dataset

Perceptron Trick

The perceptron trick, also known as the perceptron learning rule or the delta rule, is a simple algorithm used for training a binary linear classifier called the perceptron. Understanding this will help you understand logistic regression easily.

Imagine you have a scatter plot where each point represents an object, and you want to classify them as either red or blue.

The perceptron trick starts by randomly assigning some values to the weights and biases. The algorithm then goes through each object and checks if it is classified correctly based on the current weights and biases. If it is classified correctly, it moves on to the next object. But if it is misclassified, it adjusts the weights and biases in a way that moves the decision boundary closer to the misclassified object.

To make this adjustment, the algorithm looks at the misclassified object's features and modifies the weights in a direction that would correct the misclassification. It repeats this process for all the objects until it either correctly classifies all the objects or reaches a predefined maximum number of iterations.

Mathematically...

In the perceptron trick, we aim to find a decision boundary (a line in 2D or a hyperplane in higher dimensions) that separates the data points of different classes. Mathematically, this decision boundary is represented by a linear equation:

w1 * x1 + w2 * x2 + ... + wn * xn + b = 0

Here, (x1, x2, ..., xn) are the features of a data point
w1, w2, ..., wn are the corresponding weights
b is the bias term. 
The weights and bias define the orientation and position of the decision boundary.

Given a training example (X, y), where X is the feature vector and y is the true class label (-1 or 1), we want to update the weights and bias in such a way that the predicted class label matches the true class label.

The prediction is computed as

prediction = sign(np.dot(w, X) + b)

To update the weights and bias, we use the perceptron learning rule:

w_new = w + learning_rate * error * X
b_new = b + learning_rate * error
error = y - prediction

Implementation

Now we'll implement the mathematics we understood in Python:

import numpy as np

def perceptron_trick(X, y, learning_rate=0.1, max_iterations=100):
    num_features = X.shape[1]
    num_samples = X.shape[0]

    # Initialize weights and bias
    weights = np.zeros(num_features)
    bias = 0

    for _ in range(max_iterations):
        total_error = 0

        for i in range(num_samples):
            # Compute predicted class label
            prediction = np.sign(np.dot(weights, X[i]) + bias)
            if prediction != y[i]:
                weights += learning_rate * y[i] * X[i]
                bias += learning_rate * y[i]
                total_error += 1
        if total_error == 0:
            break

    return weights, bias

X = np.array([[1, 2], [2, 3], [3, 1], [4, 3]])
y = np.array([1, 1, -1, -1])

weights, bias = perceptron_trick(X, y)
print("Learned weights:", weights)
print("Learned bias:", bias)

Why do we need Logistic Regression then?

Logistic regression and the perceptron trick are both classification algorithms, but they differ in their underlying principles and capabilities.

The perceptron trick has limitations. It may not converge if the data is not linearly separable, and it does not provide probabilistic predictions or handle multi-class classification naturally.

Logistic regression addresses these limitations and extends the perceptron trick. Instead of making binary predictions directly, logistic regression models the probability of an example belonging to a particular class. It uses a logistic function (also called the sigmoid function) to map the output to a probability between 0 and 1.

Coming Soon

A comprehensive blog on logistic regression! Gain a deeper understanding of this powerful classification algorithm, building upon the foundation of the perceptron trick.

Your support matters: Like, comment, and check out the references for further study.

References:

https://www.youtube.com/@campusx-official