"Harnessing Local Binary Patterns for Image Analysis"

My first encounter with the topic I'm about to discuss with you all was in 2022, when I had a job working on a plant disease detection model with a machine learning research group in the East. While I cannot provide specific details, I can say that using local binary patterns (LBP) as a feature extraction method significantly simplified my job.

Local binary pattern (LBP) provides an effective description of texture for images by applying a threshold to the neighboring pixels based on the value of the current pixel, treating the result as a binary number. It was first introduced by Ojaja et al. in 1994 as a texture descriptor. For each pixel value in the image, a binary code is obtained by comparing its neighbourhood's intensities with the central pixel's value. A binary code is generated based on whether each neighbour's intensity is greater than or equal to a threshold. The frequency of these binary patterns is then calculated to form a histogram. Each pattern in the histogram represents a possible binary pattern found in the image. The number of histogram bins is determined by the number of pixels involved in the LBP calculation. For example, if LBP uses 8 pixels, the number of histogram bins would be 2^8, which equals 256. The basic version of the LBP operator uses the center pixel value as a threshold for the 3x3 neighboring pixels. The threshold operation creates a binary pattern representing a texture characteristic. The equation for the basic LBP can be given as follows:

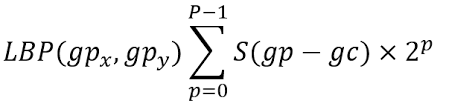
Order of operations:

Image -> Simplification -> Binarization -> PDF calculation -> Comparison

IMAGE

Of course, we need a dataset of images to extract features from images.

SIMPLIFICATION

Before creating our LBP, we need to simplify the images as part of the data preprocessing phase. This is the first step in dimensionality reduction, which allows our algorithm to focus solely on the local differences in luminance, disregarding other potential features. Therefore, we convert our image(s) into a single-channel (greyscale) representation. This creates a window for generating an LBP feature vector that represents the image.

BINARIZATION

Here, we calculate the relative local luminance changes within an image and create a low-dimensional binary representation for each pixel based on its luminance value. The process involves comparing the intensity of a central pixel with the intensities of its surrounding pixels in a defined neighborhood.

For every pixel within a given window, we select a set of k neighboring pixels from its local "neighbourhood" and compare each neighbor's intensity with the intensity of the central pixel. The direction and starting point of the comparisons are not significant as long as we maintain a consistent direction, whether clockwise or counterclockwise. As we perform these comparisons, we assign a binary value of 0 or 1 based on whether the central pixel's intensity is greater or less than the intensity of the comparison pixel, respectively. This results in a k-bit binary value, which can then be converted to a base 10 number representing a new intensity value for the corresponding pixel. This process is repeated for each pixel within the window, generating a cumulative local intensity representation in comparison to its neighboring pixels. The resulting intensity values range from 0 to 2^k, providing a reduced-dimensional Local Binary Pattern (LBP) representation of the original image.

To apply this method in practice, we need to define the LBP parameters. These parameters include the cell size, radius, and the number of comparative points (k). The cell size refers to an arbitrary MxN pixel size, which allows us to further divide the window into smaller cells. By performing LBP computations independently on each cell, we can facilitate faster and more efficient parallel processing of the image. Additionally, using overlapping cell areas enables us to capture local patterns that might be missed or fragmented if LBP were computed on the entire window. A common choice for the cell size is often 16x16 pixels.

The radius parameter determines the size of the neighborhood from which comparative pixels are sampled for each central pixel in the image. It defines the spatial extent of what we consider as "local" in the context of LBP. A larger radius implies a wider range of neighboring pixels involved in the comparisons, while a smaller radius restricts the comparison to a narrower local region.

Lastly, the k value represents the number of points within the neighbourhood that we sample for intensity comparisons. Typically, this value is set to 8, resulting in an 8-bit binary value for each pixel. Consequently, the final pixel intensity values range from 0 to 255 (2^8), providing a discrete representation of the local texture patterns.Once we have generated our k-bit LBP representations for each cell in our window, we are then ready to combine them to form our feature vectors.

It's important to note the distinction between uniform and non-uniform binary patterns generated by the Local Binary Patterns (LBP) method. Uniform patterns refer to binary numbers that exhibit a maximum of two value changes (0-1 or 1-0) throughout the pattern. For instance, patterns like 11001111, 11111110, 00011000, and 00111110 exemplify uniform binary patterns for a byte of data. Conversely, any pattern that deviates from this maximum of two changes is classified as non-uniform.The significance of distinguishing between uniform and non-uniform patterns lies in their impact on the preservation of local luminance and the rotation invariance of the encoded information. Uniform patterns offer the advantage of retaining the local luminance information at each pixel in a manner that ensures rotation invariance. This means that regardless of the orientation of the image during LBP calculation, the resulting Probability Density Function (PDF), which serves as the feature vector representation of LBP, remains consistent.

In contrast, non-uniform patterns lack the guarantee of producing the same PDF irrespective of image orientation. Consequently, using non-uniform patterns carries the risk of encoding the same image as different inputs, resulting in distinct feature patterns. Such inconsistency in feature representations could potentially undermine the integrity and reliability of the model.

Thus, the distinction between uniform and non-uniform binary patterns in LBP is crucial to ensure reliable and rotation-invariant feature representations, enabling robust and accurate analysis in various applications.

PROBABILITY DENSITY FUNCTION CALCULATION

We convert our LBP image representations into feature vectors to make them more useful and comprehensible. This conversion process involves creating a histogram, which slightly deviates from Bayesian statistics and borrows a technique commonly employed by our frequentist counterparts.

The fundamental idea is to count and quantify the occurrences of different LBP patterns within our image. We plot the results in the form of a histogram, where each bin represents a specific LBP pattern, and the corresponding count indicates how frequently that pattern appears in the image. We construct a window-level feature vector representation by aggregating the LBP representations from each cell.

The process of generating histograms and concatenating LBP representations is often abstracted away in libraries like Scikit-Image, making it easier to work with. This higher-level abstraction allows us to focus on interpreting and utilising the resulting feature vectors, rather than the intricate details of histogram computation.

These feature vectors provide a concise summary of the local texture patterns within the image, enabling effective representation and analysis. They serve as input for various machine learning algorithms, allowing us to train models and make predictions based on the extracted features.

By converting our LBP image representations into feature vectors using histograms, we gain a more interpretable and practical representation of the underlying texture patterns. This transformation enhances our ability to understand and utilize the information contained within the LBP images, facilitating tasks such as image classification, object recognition, and texture analysis.

COMPARISON

Lastly, let's dive into an important aspect of Bayesian statistical modelling: the Kullback-Leibler Divergence (KLD). This mathematical concept allows us to compare two probability density or mass functions, often represented as distributions p and q. Its purpose is to measure the difference between these distributions and shed light on how likely data points from distribution q are to come from the same underlying distribution as p. In simpler terms, KLD quantifies the discrepancy or divergence between two distributions.

The KLD, also known as D(p, q), plays a fundamental role in Bayesian analysis by providing a way to assess the similarity or dissimilarity between two sets of data. It enables us to create a new probability distribution that explains the relationship between the target distribution p and the sample distribution q. This information helps us understand the likelihood of observing the data points from distribution q, given the underlying distribution p.

However, it's important to note that KLD is not a symmetric measure, meaning that it does not determine how likely distribution p is given distribution q. Instead, it focuses solely on how likely distribution q is given distribution p. In other words, D(p, q) is not equal to D(q, p).

Understanding the essence of KLD is crucial for delving into Bayesian statistical modelling. It serves as a powerful tool for comparing and analyzing distributions, providing insights into the relationship and similarities between different datasets. Exploring the details and intricacies of KLD will be covered in a more comprehensive article, which will delve into its mathematical formulation and practical implementation.

For those eager for more concrete information, a basic implementation of KLD using the Scikit-Image library can be explored. This implementation will demonstrate how to leverage this algorithm to compare and analyze probability distributions, further enhancing your understanding of this vital concept in Bayesian statistical modelling.

Based on my experience, LBP offers several significant advantages in image analysis and classification. It allows us to generate low-dimensional representations of images that highlight local topographical characteristics. These representations can be used to classify unlabeled images by comparing their key visual features, enabling us to determine the likelihood of each image belonging to the same population.

These benefits have practical implications:

1.Low-dimensional representations: LBP allows us to create compact representations of images, simplifying the analysis process and reducing computational requirements.

2.Efficient feature extraction: LBP provides a computationally efficient method for extracting features from high-dimensional images, potentially reducing storage memory requirements.

3.Quick and accurate classification: LBP enables the creation of powerful and accurate classifiers within seconds, making it a highly efficient approach.

4.Probabilistic classification and uncertainty quantification: LBP offers a probabilistic classifier that provides true likelihoods and enables uncertainty quantification in the classification process.

While this article aims to provide a general understanding of LBP to individuals new to machine learning and statistics, it also includes details for machine learning and statistics professionals. Feel free to reach out if you have any questions.