A different approach to Matrix multiplication using Strassen's Algorithm

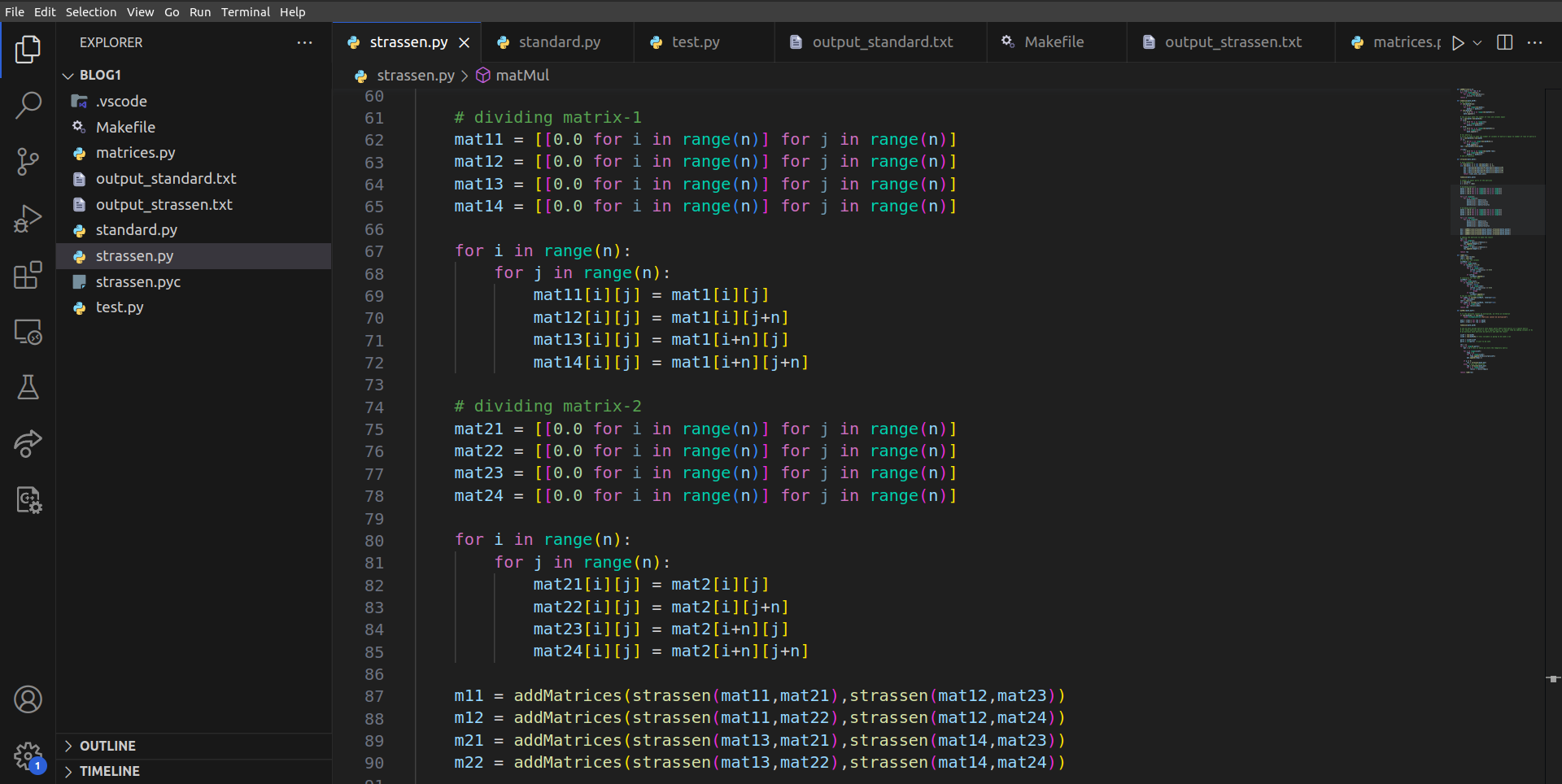
List of matrices on which we are going to run and compare our functions

# 4x4 and 4x3 matrices
mat3 = [
    [5,2,3,1],
    [7,6,4,2],
    [5,6,7,5],
    [5,7,9,7]
]
mat4 = [
    [5,2,3],
    [7,6,4],
    [5,6,7],
    [5,7,9]
]

# 3x3 and 3x3 matrices
mat5 = [
    [5,2,3],
    [7,6,4],
    [5,6,7],
]
mat6 = [
    [5,2,3],
    [7,6,5],
    [4,6,3],
]

# 5x5 and 5x4 matrices
mat7 = [
    [2,3,4,5,6],
    [3,4,5,6,7],
    [4,5,6,7,8],
    [5,6,7,8,9],
    [6,7,8,9,10],
]
mat8 = [
    [3,5,7,9],
    [5,8,11,14],
    [7,11,15,19],
    [9,14,19,24],
    [11,17,23,29],
]

# 5x8 matrix
mat9 = [
    [3,5,7,9,11,13,15],
    [5,8,11,14,17,20,23],
    [7,11,15,19,23,27,31],
    [9,14,19,24,29,34,39],
    [11,17,23,29,35,41,47],
]

Output using Strassen's Algorithm

Time taken : 229.83551025390625 µs
59 47 53 
107 88 91 
127 123 133 
154 155 169 

Time taken : 168.5619354248047 µs
51 40 34 
93 74 63 
95 88 66 

Time taken : 955.3432464599609 µs
160 250 340 430 
195 305 415 525 
230 360 490 620 
265 415 565 715 
300 470 640 810 

Time taken : 1618.1468963623047 µs
160 250 340 430 520 610 700 
195 305 415 525 635 745 855 
230 360 490 620 750 880 1010 
265 415 565 715 865 1015 1165 
300 470 640 810 980 1150 1320

Output using Standard Matrix Multiplication

Time taken : 34.57069396972656 µs
59 47 53 
107 88 91 
127 123 133 
154 155 169 

Time taken : 18.835067749023438 µs
51 40 34 
93 74 63 
95 88 66 

Time taken : 42.67692565917969 µs
160 250 340 430 
195 305 415 525 
230 360 490 620 
265 415 565 715 
300 470 640 810 

Time taken : 75.34027099609375 µs
160 250 340 430 520 610 700 
195 305 415 525 635 745 855 
230 360 490 620 750 880 1010 
265 415 565 715 865 1015 1165 
300 470 640 810 980 1150 1320

View this project on Replit and GitHub

Conclusion

As we can see, our traditional approach to matrix multiplication is way faster than this approach (due to its recursive nature). But for larger matrices things change

---