Given a matrix of dimensions n x n having elements 1 to n*n distinct elements, check whether the matrix is magic square or not.

A magic square is a square that has the same sum along all rows, columns and diagonals. Input format There are n + 1 lines of input. The first line contains the integer n. The next n lines contain n space-separated elements. Output format Print "Yes" if it is a magic square, "No" otherwise.

Milestone 1: Understand the problem clearly

1. We need to check whether the given square matrix is a magic square or not. A magic square is a square matrix where the sum of all rows, columns, and diagonals is the same.

2. We are given the size of the square matrix 'n' and the matrix elements.

Milestone 2: Finalize approach & execution plan

1. To check if the given matrix is a magic square, we need to calculate the expected sum of each row, column, and diagonals.

2. The expected sum can be calculated as (n * (n^2 + 1)) / 2.

3. Then, we will sum up each row, each column, and both diagonals and compare them with the expected sum.

4. If all these sums are equal to the expected sum, we will return "Yes," indicating that it's a magic square; otherwise, we will return "No."

Milestone 3: Come up with an Instruction Manual for a 10-year-old Let's write the high-level logic as a detailed instruction manual for a 10-year-old:

1. Read the value of 'n' from the input.

2. Create a 2D array named 'grid' with dimensions n x n.

3. Read the matrix elements and store them in the 'grid' array.

4. Calculate the expected sum as (n * (n^2 + 1)) / 2 and store it in a variable named 'expected.'

5. Initialize variables for the sum of rows, columns, and diagonals, all set to 0.

6. Loop through each row in the 'grid':

   • Calculate the sum of the current row and store it in the variable for the row sum.

   • If the row sum is not equal to the expected sum, return "No."

7. Loop through each column in the 'grid':

   • Calculate the sum of the current column and store it in the variable for the column sum.

   • If the column sum is not equal to the expected sum, return "No."

8. Calculate the sum of the main diagonal (top-left to bottom-right) and store it in a variable.

   • If the diagonal sum is not equal to the expected sum, return "No."

9. Calculate the sum of the secondary diagonal (top-right to bottom-left) and store it in a variable.

   • If the diagonal sum is not equal to the expected sum, return "No."

10. If all the sums are equal to the expected sum, return "Yes."

Milestone 4: Code by expanding your 10-year-old's "Instruction Manual" Let's translate the above instruction manual into Java code:

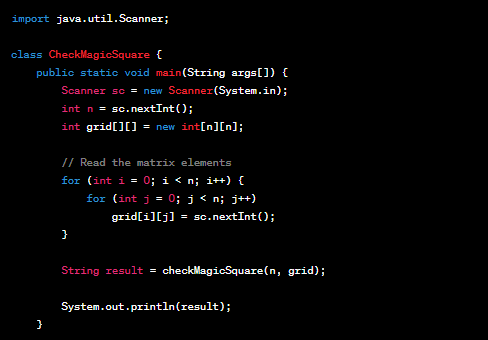
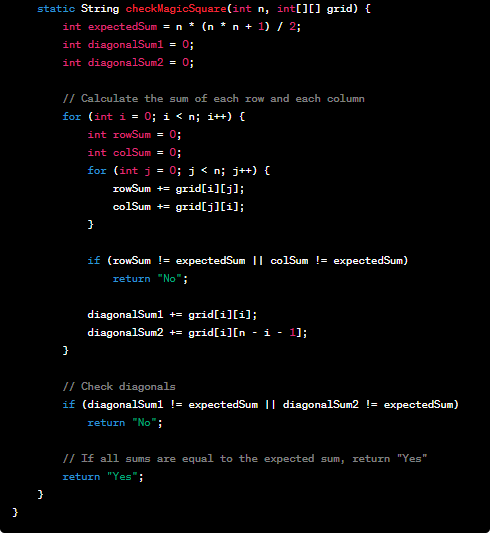
Milestone 5: Prove that your code works using custom test cases Now you can test the code with custom test cases, including edge cases, to ensure it's working correctly. The constraints for this problem are relatively small, so you can try matrices of various sizes and combinations of elements to check the correctness of the code.

I hope this helps! If you have any further questions or need clarification, feel free to ask. Happy coding!