Static Program Analysis PA-1
 bear
bear
1 Assignment Objectives
Implement a live variable analysis for Java.
Implement a generic solver, which will be used to solve the data-flow problem you defined, i.e., the live variable.
2 Get Familiar with Major Classes
pascal.taie.analysis.dataflow.analysis.DataflowAnalysis
which contains 7 APIs:
1 boolean isForward()
2 Fact newBoundaryFact(CFG<Node> cfg)
3 Fact newInitialFact()
4 void meetInto(Fact fact, Fact target)
5 boolean transferNode(Node node, Fact in, Fact out)
6 boolean needTransferEdge(Edge<Node> edge)
7 Fact transferEdge(Edge<Node> edge, Fact nodeFact)
pascal.taie.ir.exp.Exp
This is one of two key interfaces in Tai-e's IR (another one is Stmt) which represents all expressions in the program.
Type getType()
default List<RValue> getUses() { return List.of(); }
<T> T accept(ExpVisitor<T> visitor)
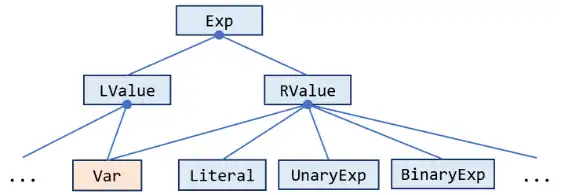
we classify all expressions into two kinds, LValue and RValue.
pascal.taie.ir.stmt.Stmt
which represents all statements in the program. Each expression belongs to a certain statement in a typical programming language.
Optional<LValue> getDef()
List<RValue> getUses()
Each Stmt can define at most one value and use zero or more values, and thus we Optional and List to wrap the result of getDef() and getUses().
pascal.taie.analysis.dataflow.fact.SetFact<Var>
which provides various set operations, e.g., add/remove elements, intersect/union with other sets, etc. We will use this class to represent the data facts in live variable analysis.
pascal.taie.analysis.dataflow.analysis.LiveVariableAnalysis
This class implements DataflowAnalysis and defines live variable analysis.
3 Task-1 Implement LiveVariableAnalysis:
SetFact newBoundaryFact(CFG)
SetFact newInitialFact()
void meetInto(SetFact, SetFact)
boolean transferNode(Stmt, SetFact, SetFact)
which correspond to four parts of the live variable analysis algorithm as shown below:
IN[exit] = null; <- newBoundaryFact()
for (each basic block b other then exit)
IN[b] = null; <- newInitialFact()
while (changes to any IN occur)
for (each basic block b other then exit) {
OUT[b] = ∪(s a successor of b) IN[s]; <- meetInto()
IN[b] = use[b] ∪ (OUT[b] - def[b]); <- transferNode()
}
As for SetFact newBoundaryFact(CFG) and SetFact newInitialFact()
Since we are analyzing from the bottom of the lattice upwards, the initial value of both boundary and IN facts is the empty set.
@Override
public SetFact<Var> newBoundaryFact(CFG<Stmt> cfg) {
return new SetFact<>();
}
@Override
public SetFact<Var> newInitialFact() {
return new SetFact<>();
}
As for void meetInto(SetFact fact, SetFact target)
Since SetFact is a wrapper around Set API, we just add all the items of fact to the target.
@Override
public void meetInto(SetFact<Var> fact, SetFact<Var> target) {
target.union(fact);
}
As for boolean transferNode(Stmt, SetFact, SetFact)
Get familiar with IN[B] - def[B] + use[B] !!!
@Override
public boolean transferNode(Stmt stmt, SetFact<Var> in, SetFact<Var> out) {
SetFact<Var> copy = out.copy();
Optional<LValue> def = stmt.getDef();
List<RValue> uses = stmt.getUses();
// in[b] - def[b]
if (def.isPresent() && def.get() instanceof Var var) {
copy.remove(var);
}
// + use[b]
for (RValue rvalue : uses) {
if (rvalue instanceof Var var)
copy.add(var);
}
// judge whether changed
boolean changed = !in.equals(copy);
if (changed) {
in.union(copy); // in.set(copy);
}
return changed;
}
4 Task-2 Implement Iterative Solver
pascal.taie.analysis.dataflow.fact.DataflowResult
pascal.taie.analysis.graph.cfg.CFG
pascal.taie.analysis.dataflow.solver.Solver
The core method for the whole analysis is according to the algorithm below:
while (changes to any IN occur)
for (each basic block b other then exit) {
OUT[b] = ∪(s a successor of b) IN[s]; <- meetInto()
IN[b] = use[b] ∪ (OUT[b] - def[b]); <- transferNode()
}
protected void doSolveBackward(CFG<Node> cfg, DataflowResult<Node, Fact> result) {
boolean changed = true; // changes to any IN occur
while (changed)
{
changed = false;
for (Node node : cfg) {
Fact out = result.getOutFact(node);
Fact in = result.getInFact(node);
// out[b] = ∪ (s a successor of b) in[s]
for (Node succ : cfg.getSuccsOf(node)) {
analysis.meetInto(result.getInFact(succ), out);
}
// in[b] = in[b] - def[b] + def[b]
if(analysis.transferNode(node, in, out)) {
changed = true;
}
result.setOutFact(node, out);
result.setInFact(node, in);
}
}
}
5 Analysis Result
We use the self-implemented analyzer to analyze an example code(Assign.java)
class Assign {
int assign(int a, int b, int c) {
int d = a + b;
b = d;
c = a;
return b;
}
}
The analysis process is as follows
Tai-e starts ...
Writing options to output\options.yml
WorldBuilder starts ...
Warning: main class 'Assign' does not have main(String[]) method!
9836 classes with 97661 methods in the world
WorldBuilder finishes, elapsed time: 6.05s
throw starts ...
1 classes in scope (app) of class analyses
2 methods in scope (app) of method analyses
throw finishes, elapsed time: 0.04s
cfg starts ...
cfg finishes, elapsed time: 0.03s
livevar starts ...
livevar finishes, elapsed time: 0.01s
process-result starts ...
-------------------- <Assign: void <init>()> (livevar) --------------------
[0@L1] invokespecial %this.<java.lang.Object: void <init>()>(); []
[1@L1] return; []
-------------------- <Assign: int assign(int,int,int)> (livevar) --------------------
[0@L4] d = a + b; [a, d]
[1@L5] b = d; [a, b]
[2@L6] c = a; [b]
[3@L7] return b; []
process-result finishes, elapsed time: 0.02s
Tai-e finishes, elapsed time: 6.41s
Let's extract the results, everything is obvious.
[0@L4] d = a + b; [a, d]
[1@L5] b = d; [a, b]
[2@L6] c = a; [b]
[3@L7] return b; []
That's all, Thanks. 🐻
Subscribe to my newsletter
Read articles from bear directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

bear
bear
bear with us, while we think.