What is LCA(Lowest Common Ancestor)

Definition

Lowest Common Ancestor, LCA.

LCA is an algorithm or concept used in tree structures to find the closest common ancestor of two nodes.

Example

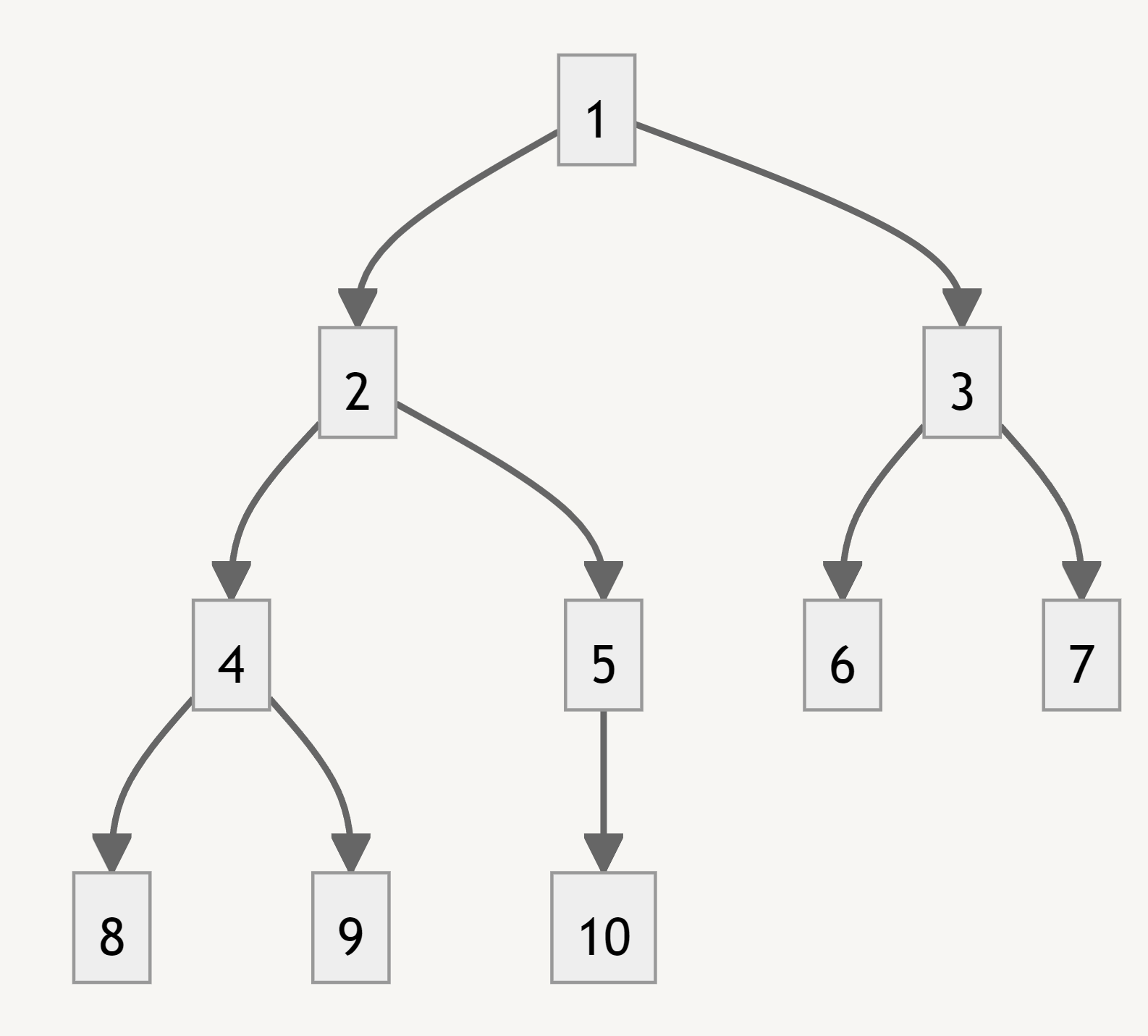
In the above binary tree, the LCA of 4 and 6 is 1.

LCA(4, 6) = 1

Purpose

The purpose of the LCA is to efficiently find the closest common ancestor of two nodes in a tree structure.

Cases to consider using LCA

You should consider using the LCA algorithm in the following cases:

• When you need to calculate the distance between two nodes in a tree structure.

• When you need to find nodes belonging to a subtree rooted at a specific node.

• When calculating the shortest path in computer networks.

• When solving collision detection and other problems in game development.

Cases not suitable for using LCA

The LCA algorithm is limited to tree structures and cannot be used in other data structures. Additionally, if the problem doesn't involve finding the common ancestor of two nodes, there is no need to use LCA.

Advantages

• It can efficiently find the LCA of two nodes with a reasonable time complexity.

• After preprocessing, query operations can be performed quickly.

Disadvantages

• The LCA algorithm is restricted to tree structures and cannot be applied to other data structures.

Implementation Steps

1. Compute the parent and depth information for each node in the binary tree.

2. This step is called preprocessing.

3. Move towards the parents of the two nodes for which you want to find the LCA.

4. While moving towards the parents, check for the first intersection of the nodes.

5. The first intersection is the LCA.

Example

import java.util.ArrayList;
import java.util.List;

class Node {
    int value;
    Node parent;
    List<Node> children;

    Node(int value) {
        this.value = value;
        this.children = new ArrayList<>();
    }
}

public class LCAExample {

    private static void preprocess(Node node, Node parent, int depth) {
        node.parent = parent;

        for (Node child : node.children) {
            preprocess(child, node, depth + 1);
        }
    }

    private static Node findLCA(Node node1, Node node2) {
        int depth1 = getDepth(node1);
        int depth2 = getDepth(node2);

        while (depth1 > depth2) {
            node1 = node1.parent;
            depth1--;
        }

        while (depth2 > depth1) {
            node2 = node2.parent;
            depth2--;
        }

        while (node1 != node2) {
            node1 = node1.parent;
            node2 = node2.parent;
        }

        return node1;
    }

    private static int getDepth(Node node) {
        int depth = 0;
        while (node.parent != null) {
            node = node.parent;
            depth++;
        }
        return depth;
    }

    public static void main(String[] args) {
        Node root = new Node(1);
        Node node2 = new Node(2);
        Node node3 = new Node(3);
        Node node4 = new Node(4);
        Node node5 = new Node(5);
        Node node6 = new Node(6);
        Node node7 = new Node(7);

        root.children.add(node2);
        root.children.add(node3);
        node2.children.add(node4);
        node2.children.add(node5);
        node3.children.add(node6);
        node3.children.add(node7);

        preprocess(root, null, 0);

        Node lcaNode = findLCA(node4, node5);
        System.out.println("LCA: " + lcaNode.value); // 2

        lcaNode = findLCA(node4, node6);
        System.out.println("LCA: " + lcaNode.value); // 1

        lcaNode = findLCA(node3, node7);
        System.out.println("LCA: " + lcaNode.value); // 3
    }
}