1 Assignment Objectives

Implement a constant propagation for Java
Implement a generic worklist solver, which will be used to solve the data-flow problem you defined, i.e., constant propagation.
Assignment-SPA-Nanjing-University
GitHub-Code-SPA-Nanjing University

2 Basics to Know in Advance

Since the values of types boolean, byte, char, and short are also represented and computed as int values during run time, thus our analysis could handle the values of these types, not just the int type.

We only need to focus on the assigned statements whose left-hand side expressions are variables, and whose right-hand side expressions are:

Constants, e.g., x = 1

Variables, e.g., x = y

Binary expressions, e.g., x = a + b, and x = a >> b

For binary operations, we need to handle these operators:

Arithmetic: +, -, *, /, %

Condition: ==, !=, <, >, <=, >=

Shift: <<, >>, >>>

Bitwise: |, &, ^

Conservative Approximations

For the assigned statements(again, whose left-hand side expressions are variables) with other right-hand expressions, e.g., method calls (x = m(...)) or field loads (x = o.f), you should give them conservative approximations, e.g., x = NAC.

pascal.taie.ir.IR

this class is the central data structure of intermediate representation in Tai-e, and each IR instance contains the information for the body of a particular method, such as variables, parameters, statements, etc. You can obtain this information through its APIs, which are all commented on in the source code.
pascal.taie.ir.exp.Exp
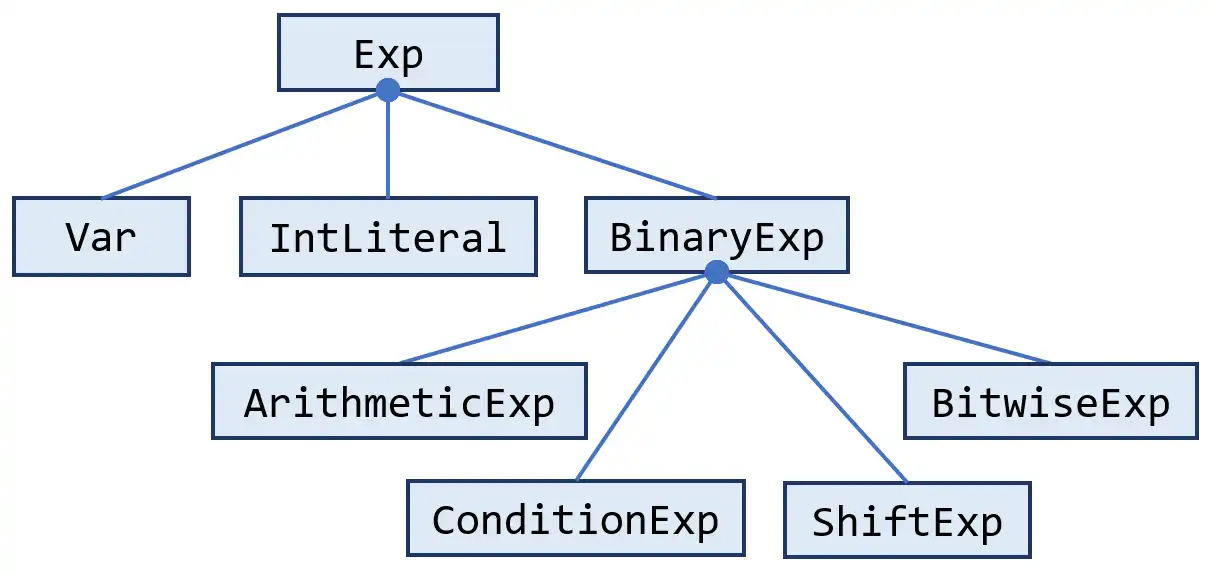
pascal.taie.ir.exp.Var

which represents the variables in Tai-e's IR.
pascal.taie.ir.exp.IntLiteral

Each instance of this class represents an integer literal in the program, and we can obtain the int value by calling its getValues() method.
pascal.taie.ir.exp.BinaryExp

This class represents binary expression in the program, and it has several subclasses, corresponding to different expressions as shown above.
pascal.taie.ir.stmt.DefinitionStmt

also called assigned statements.
pascal.taie.analysis.dataflow.analysis.DataflowAnalysis

An important class that needs no introduction.
pascal.taie.analysis.dataflow.analysis.constprop.Value
- Value getNAC(): Returns NAC
- Value getUndef(): Returns UNDEF
- Value makeConstant(int): Returns a constant for the given integer
pascal.taie.analysis.dataflow.analysis.constprop.CPFact

This class represents the data facts in constant propagation, i.e., the mapping from variables (Var) to their lattice values (Value). This class provides various map-related operations, such as query/update key-value mappings, etc., and most of them are inherited from pascal.taie.analysis.dataflow.fact.MapFact. The APIs of both classes are commented on in the source code, and you should read the source code and decide which APIs to use in this assignment.
pascal.taie.analysis.dataflow.analysis.constprop.ConstantPropagation

This is an important class we should implement.

4 Task-1 Implement ConstantPropagation

Implement the following APIs of ConstantPropagation

CPFact newBoundaryFact(CFG)
CPFact newInitialFact()
void meetInto(CPFact,CPFact)

Before dealing with this method, implement Value meetValue(Value, Value) first.
boolean transferNode(Stmt,CPFact,CPFact)

Before dealing with this method, implement Value evaluate(Exp, CPFact) first.

Let's get familiar with constantPropagation first:

Given a variable x at program point p, determine whether x is guaranteed to hold a constant value at p.

As we said before, static program analysis mainly contains two parts

Abstraction Fact can be represented as SetFact<Pair<Var, Value>>, and in Tai-e's implementations, which is represented as CPFact (extends MapFact<Var, Value>)
Safe-Approximation
- Transfer Function: Given DefinitionStmt x = ...,
  
  OUT[B] = (IN[B] - Pair<x, _>) + gen(B), and as for gen(B) it can be discussed in different contexts.
- ```
        1. x = 1 
        // x is assigned to literal, and gen(B) = {<x, 1>}

        2. x = y 
        // x is assigned to variable, and gen(B) = {<x, val(y)>}

        3. x = a op b 
        // x is assigned to an expression, then we need to exaluate
        // the whole expression gen(B) = {<x, f(a, b)>}
```
  As for the third condition, f(a, b) can be divided into three parts:
  
  (1) Val(a) op Val(b), when both a and b are literal, it's straightforward to do the math.
  
  (2) NAC, when at least one of a and b is NAC.
  
  (3) UNDEF, other situations.
Control of Flow: OUT[S1], OUT[S2], ..., OUT[Sn] -> IN[B] The first thing we should clear is that each OUT (or IN) Fact is a set of Pair<Var, Value> (mapping relation from Var to Value)

      Fact: { <var1, value1>, <var2, value2>, ..., <varn, valuen>}

Ignoring for a moment whether the merge operation is ∪ or ∩, let's consider that for IN[B1] and IN[B2] the merge is done by taking out the Pair with the same key values from their respective sets and merging their values. For example,

        Fact1 = { <x, 10>, <y, 10>, <z, 10>}
        Fact2 = { <x, 10>, <y, NAC>, <z, 20>}
        // After merging, we get the result
        Fact_Merge = { <x, 10>, <y, NAC>, <z, NAC>}

5 Task-2 Worklist Algorithm

Similar to PA-1, we need to get familiar with DataflowResult, CFG, and Solver classes.

DataflowResult An object which manages the data flow associated with nodes.

CFG Representation of the control-flow graph of a method.

Solver Base class for data flow analysis solver, which provides common functionalities for different solver implementations.

Besides, we need to know pascal.taie.analysis.dataflow.solver.WorkListSolver

After that, we can implement the WorkList Algorithm for Constant Propagation according to the lecture described:

OUT[entry] = ∅;
for (each basic block B\entry)
    OUT[B] = ∅;
Worklist ← all basic blocks
while (Worklist is not empty)
    Pick a basic block B from Worklist
    old_OUT = OUT[B]
    IN[B] = ⊔P a predecessor of B OUT[P];
    OUT[B] = genB U (IN[B] - killB);
    if (old_OUT ≠ OUT[B])
        Add all successors of B to Worklist

After implementing the algorithm, we can have a look at the result:

Tai-e starts ...
Writing options to output\options.yml
WorldBuilder starts ...
Warning: main class 'Assign' does not have main(String[]) method!
9836 classes with 97661 methods in the world
WorldBuilder finishes, elapsed time: 6.98s
throw starts ...
1 classes in scope (app) of class analyses
2 methods in scope (app) of method analyses
throw finishes, elapsed time: 0.07s
cfg starts ...
cfg finishes, elapsed time: 0.04s
constprop starts ...
in is {}
in is {x=1}
in is {x=2}
in is {x=3}
in is {x=4}
in is {%intconst0=6, x=4}
constprop finishes, elapsed time: 0.01s
process-result starts ...
-------------------- <Assign: void <init>()> (constprop) --------------------
[0@L1] invokespecial %this.<java.lang.Object: void <init>()>(); {}
[1@L1] return; {}

-------------------- <Assign: void assign()> (constprop) --------------------
[0@L4] x = 1; {x=1}
[1@L5] x = 2; {x=2}
[2@L6] x = 3; {x=3}
[3@L7] x = 4; {x=4}
[4@L8] %intconst0 = 6; {%intconst0=6, x=4}
[5@L8] y = x + %intconst0; {%intconst0=6, x=4, y=10}
[6@L8] return; {%intconst0=6, x=4, y=10}

process-result finishes, elapsed time: 0.01s
Tai-e finishes, elapsed time: 7.30s

Submit

Fourth Submit:

Judge Log
Analyze 52 methods, pass 48 methods
There are 481 Stmts in all test cases
Your submission correctly analyzes 467 Stmts


[!] Failed on [hidden] testcase(s)
Tips: we will not give you any information about [hidden] testcase(s)

That's all, thanks!

REFERENCE

GitHub-reference

Lecture-Notes-Constant-Propagation-Stanford-University

Static Program Analysis PA-2

Table of contents

1 Assignment Objectives

2 Basics to Know in Advance

4 Task-1 Implement ConstantPropagation

5 Task-2 Worklist Algorithm

REFERENCE

Subscribe to my newsletter

bear

bear

Static Program Analysis PA-2

Table of contents

1 Assignment Objectives

2 Basics to Know in Advance

3 RTFC -- IR-related classes

4 Task-1 Implement ConstantPropagation

5 Task-2 Worklist Algorithm

REFERENCE

Subscribe to my newsletter

bear

bear