"Cracking the Code of Maximum Subarray Sum: Kadane's Algorithm"

Introduction

Picture yourself in a tech interview, where your coding abilities are under a magnifying glass. One puzzle that frequently appears is the "Maximum Subarray Sum." Don't let the name intimidate you – it's a challenge that's important for interviews at major tech companies.

Companies like Google, Facebook, and Amazon love this problem. It's not just about numbers; it's about showing how well you can think critically and come up with efficient solutions.

In this journey, we'll unlock the mystery of Kadane's Algorithm, which is a clever way to tackle the Maximum Subarray Sum problem. We'll also find out why tech companies adore asking about it in interviews. We'll keep it simple, exploring the algorithm step by step. By the end, you'll be all set to tackle this problem and impress in your technical interviews. Let's jump into the world of Kadane's Algorithm and make tech interviews a breeze.

Problem Statement

The Maximum Subarray Sum problem revolves around finding a contiguous subarray within a given array that carries the largest sum. In simpler terms, given an array of integers, we need to identify a sequence of numbers that, when summed up, results in the maximum possible value. This is an interesting challenge that often appears in technical interviews, particularly with renowned tech companies such as Google, Facebook, and Amazon.

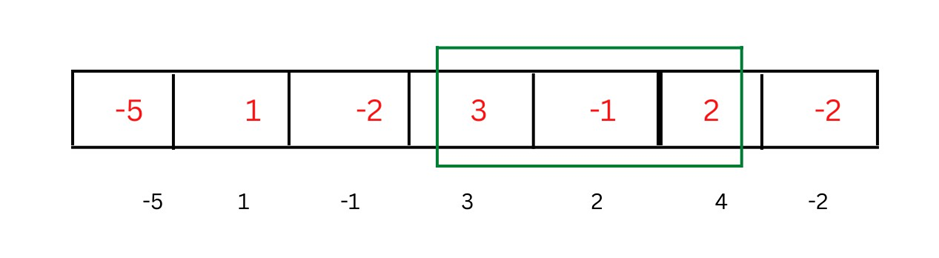
Example Scenarios

Example 1:

Input: nums = [-2,1,-3,4,-1,2,1,-5,4]

Output: 6

Explanation: The subarray [4,-1,2,1] has the largest sum of 6.

Example 2:

Input: nums = [1]

Output: 1

Explanation: The subarray [1] has the largest sum of 1.

Example 3:

Input: nums = [5,4,-1,7,8]

Output: 23

Explanation: The subarray [5,4,-1,7,8] has the largest sum of 23.

Simple Approach: Brute Force

The simplest approach to solve the Maximum Subarray Sum problem is to systematically evaluate every possible subarray and determine the maximum sum among them. While this method might not be the most efficient, it offers a straightforward way to grasp the essence of the problem before diving into more optimized solutions like Kadane's Algorithm.

Here's how the brute force approach works:

1. Initialize a variable maxSum to keep track of the maximum sum encountered during the process.

2. Loop through each element in the array using an outer loop with an index i from 0 to n - 1, where n is the size of the array.

3. For each i, initiate an inner loop with an index j starting from i to n - 1.

4. In the inner loop, calculate the sum of the subarray from index i to index j, continuously adding the values of the elements in this range to a variable currentSum.

5. Compare the value of currentSum with the current maxSum. If currentSum is greater, update maxSum to the value of currentSum.

6. After the inner loop finishes for a particular i, move to the next element in the outer loop and repeat the process.

7. Once both loops have run through all possible subarrays, the maxSum will hold the maximum sum of all contiguous subarrays.

8. Return the value of maxSum as the final result.

While this method is straightforward to understand, it can be computationally expensive for larger arrays due to the nested loops. As we progress in our exploration, we'll uncover the ingenious Kadane's Algorithm, which dramatically improves the efficiency of solving the Maximum Subarray Sum problem.

def maximumSubarraySum(arr):
    n = len(arr)
    maxSum = float('-inf')

    for i in range(n):
        currSum = 0

        for j in range(i, n):
            currSum += arr[j]
            maxSum = max(maxSum, currSum)

    return maxSum

if __name__ == "__main__":
    a = [1, 3, 8, -2, 6, -8, 5]
    print(maximumSubarraySum(a))

Time complexity: O(N^2), Where N is the size of the array.
Space complexity: O(1)

Efficient Approach: Kadane’s Algorithm

Kadane's Algorithm stands as an iterative dynamic programming technique, designed to efficiently determine the maximum sum subarray within an array. It achieves this by calculating the maximum sum subarray that concludes at a given position, utilizing information from the maximum sum subarray ending at the previous position. The following steps illustrate the algorithm's solution to the problem:

1. Define two variables: currSum, responsible for storing the maximum sum ending at the current position, and maxSum, dedicated to holding the maximum sum encountered overall.

2. Initialize currSum with 0 and maxSum with INT_MIN (negative infinity), ensuring a baseline for comparison.

3. Iterate over the entire array, element by element, and update currSum as follows:

   • Add the value of the current element to currSum.

   • Compare currSum with maxSum:

     • If currSum is greater than maxSum, update maxSum with the value of currSum.

     • If currSum is less than zero, reset it to zero. This step ensures that negative subarray sums are excluded, as they won't contribute positively to the maximum sum.

4. After completing the iteration, maxSum will hold the maximum sum of all contiguous subarrays.

5. Finally, print the value of maxSum.

Through this systematic approach, Kadane's Algorithm efficiently identifies the maximum subarray sum without resorting to exhaustive computations, making it an essential tool for tackling the Maximum Subarray Sum problem.

def maximumSubarraySum(arr):
    n = len(arr)
    maxSum = -1e8     # Initialize maxSum to a very small value
    currSum = 0       # Initialize currSum to track the current subarray sum

    for i in range(n):
        currSum += arr[i]      # Add the current element to currSum

        if currSum > maxSum:   # Update maxSum if currSum is larger
            maxSum = currSum

        if currSum < 0:        # Reset currSum to zero if it becomes negative
            currSum = 0

    return maxSum

if __name__ == "__main__":
    # Your code goes here
    print(maximumSubarraySum([1, 3, 8, -2, 6, -8, 5]))

Time complexity: O(N), Where N is the size of the array.
Space complexity: O(N)

Conclusion

In the realm of technical interviews, mastering problem-solving is key. Our exploration of the Maximum Subarray Sum problem has uncovered Kadane's Algorithm—a dynamic programming gem. From basic methods to efficient solutions, you've seen algorithms evolve to conquer challenges.

Now, you're ready to confidently tackle this problem and others. It's about nurturing your problem-solving skills and thinking critically. As you step into technical interviews, approach each question as a strategic problem-solver. Your coding journey has begun, and armed with these techniques, you're set to shine in tech interviews.

Wishing you success and growth in your coding journey!