🔰 ShaderGraph can bloat your shaders, and here is when

Introduction

Since the rise of new rendering pipelines in Unity Engine developers have been incentivized to create graphical shaders using a tool called ShaderGraph since hand-writing such shaders is no longer as simple as in Legacy RP + Unity's SRP shader docs don't help at all with new macros, functions & code conventions.

ShaderGraph certainly simplifies shader creation for many developers and also many devs found out they actually enjoy creating shaders thanks to it.

Most developers and artists take all of ShaderGraph's nodes and settings for granted but have you ever wondered if the HLSL code behind them is actually efficiently written? Every graphical tool which is created as an abstraction over any code base or API will most likely create unnecessary (redundant) code behind the scenes and that's exactly what I will be showing you today using Unity 2022.3.2f1 (LTS) and HDRP version 14.0.8.

Before we start

To measure HLSL code efficiency I decided to use AMD Radeon GPU Analyzer which when used as an offline shader compiler, allows developers to see ISA disassembly as well as the number of clock cycles each instruction needs.

Of course, the amount of instructions as well as their cycle counts is only a general indicator of the efficiency of your code. There are many other factors that come into play such as the number of cores your GPU has, occupancy, throughput and many others.

For the sake of simplicity, I chose ISA instruction amount and a total clock cycle count as my metrics. In short: the lesser amount of ISA instructions and clock cycles, the quicker the GPU executes a given shader.

List of Abbreviations

(S)RP - (Scriptable) Rendering Pipeline

SG - Shader Graph

LTS - Long Term Support

ISA - Instruction Set Architecture

RGA - Radeon GPU Analyzer by AMD

RDNA2 - GPU microarchitecture designed by AMD

D3D11 / 12 - Rendering APIs Direct3D 11 & Direct3D 12

FXC - Older shader compiler for D3D11

DXC - Modern shader compiler for D3D12

GPU - Graphics Processing Unit

Rotate (UVs)

Sometimes we just need to rotate those UVs and a convenient way to do so is via Rotate Node.

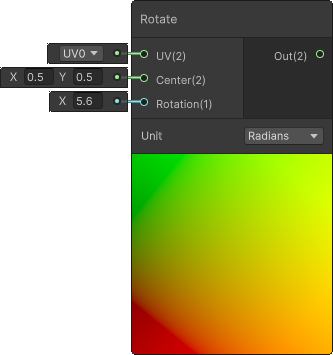
This node generates the following HLSL code:

void Unity_Rotate_Radians_float(float2 UV, float2 Center, float Rotation, out float2 Out)
{
    //rotation matrix
    UV -= Center;
    float s = sin(Rotation);
    float c = cos(Rotation);

    //center rotation matrix
    float2x2 rMatrix = float2x2(c, -s, s, c);
    rMatrix *= 0.5;
    rMatrix += 0.5;
    rMatrix = rMatrix * 2 - 1;

    //multiply the UVs by the rotation matrix
    UV.xy = mul(UV.xy, rMatrix);
    UV += Center;

    Out = UV;
}

The raw ISA disassembly of this function looks like this:

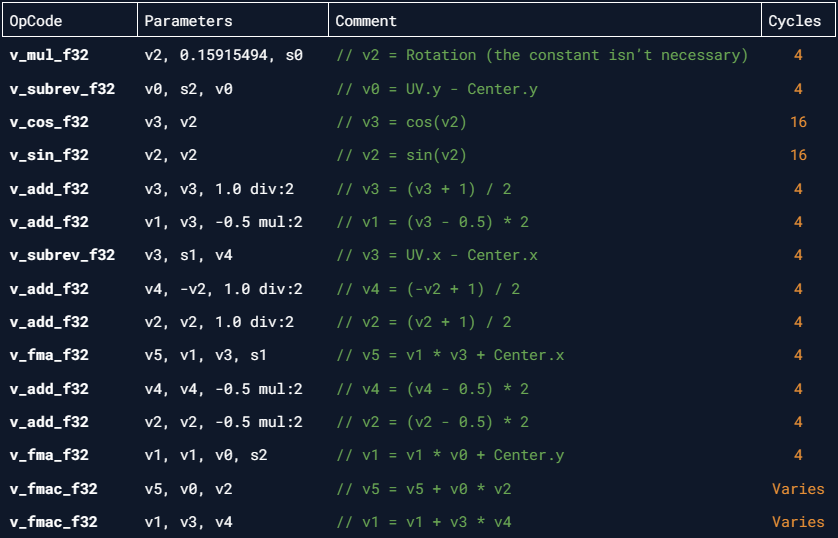
In total it costs at least 73 clock cycles. Can you spot the redundancy?

// These 2 lines remap 'rMatrix' values from [-1, 1] range to [0, 1] range
rMatrix *= 0.5;
rMatrix += 0.5;

// This line remaps 'rMatrix' values from [0, 1] range back to [-1, 1]
rMatrix = rMatrix * 2 - 1;

Why are these 3 lines necessary? I have no clue why Unity team decided to put them in but since they are inverse operations of one another, removing this junk doesn't affect the output of the shader at all. Maybe it's some old forgotten code related to something which is long removed? Nobody probably knows.

After cleanup:

float2 RotateUVs(float2 uv, float2 center, float rotation)
{
    uv -= center;

    float s = sin(rotation);
    float c = cos(rotation);
    // One could also use 'sincos(rotation, s, c)' function

    float2x2 rotMatrix = float2x2(c, -s, s, c);
    return mul(uv, rotMatrix) + center;
}

And the ISA disassembly view:

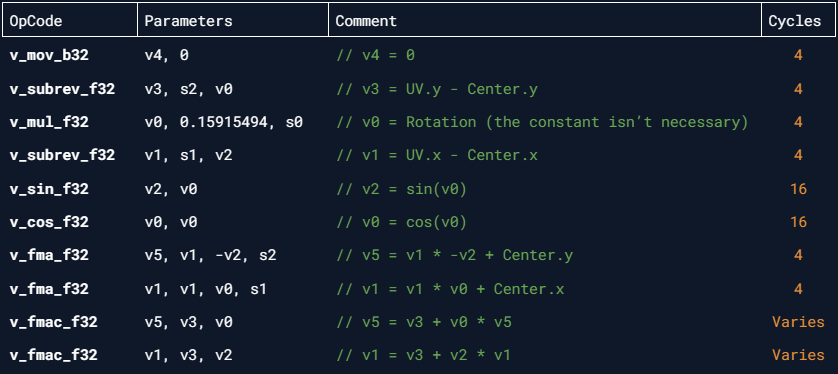
Now the simplified function costs at least 56 clock cycles which is a decent update.

Reason

When constructing a 2D rotation matrix you have to use sin and cos and since these functions return values in the range of [-1, 1], it's unnecessary to remap them to [0, 1] using x = x * 0.5 + 0.5 and then back to [-1, 1] using x = x * 2 - 1.

Sometimes the compiler is smart enough to produce fast assembly even with such redundant code but keep in mind you might not be that lucky next time.

Remarks

Just out of curiosity, I've translated the FXC compiled shader back into HLSL and this is how the FXC simplified my code:

float2 RotateUVs(float2 uv, float2 center, float rotation)
{
    uv -= center;

    float s, c;
    sincos(rotation, s, c);

    float3 r3 = float3(-s, c, s);
    float2 r1;

    r1.y = dot(UV, r3.xy);
    r1.x = dot(UV, r3.yz);

    return r1 + center;
}

It replaced the 2D matrix multiplication function with 2 dot products, which is logical since that's how the math for 2D matrix-vector multiplication works and with such a change it skipped a lot of unnecessary cycles on executing a mul() call.

Rotate About Axis

Rotate about axis might not be used as often but I certainly found it useful recently when I needed to rotate GPU-instanced grass blades around the terrain's surface normal.

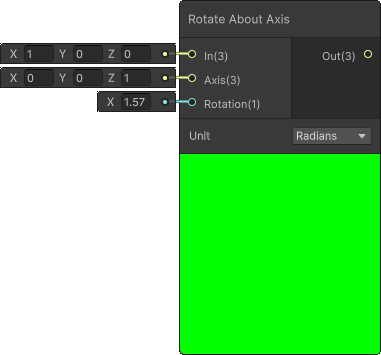
Here's a code we get from SG:

void Unity_RotateAboutAxis_Radians_float(float3 In, float3 Axis, float Rotation, out float3 Out)
{
    float s = sin(Rotation);
    float c = cos(Rotation);
    float one_minus_c = 1.0 - c;

    Axis = normalize(Axis);

    float3x3 rot_mat =
    {   one_minus_c * Axis.x * Axis.x + c, one_minus_c * Axis.x * Axis.y - Axis.z * s, one_minus_c * Axis.z * Axis.x + Axis.y * s,
        one_minus_c * Axis.x * Axis.y + Axis.z * s, one_minus_c * Axis.y * Axis.y + c, one_minus_c * Axis.y * Axis.z - Axis.x * s,
        one_minus_c * Axis.z * Axis.x - Axis.y * s, one_minus_c * Axis.y * Axis.z + Axis.x * s, one_minus_c * Axis.z * Axis.z + c
    };
    Out = mul(rot_mat,  In);
}

It is a pretty standard way of calculating such rotation vector but since the ISA disassembly is quite long for this one, I will summarize everything at the end of this section after asking my favorite question... can we simplify this?

Well, using Rodrigues' rotation formula we can simplify the code to just 3 lines:

float3 RotateAroundAxis(float3 v, float3 axis, float angle)
{
    float c = cos(angle);
    float s = sin(angle);
    return v * c + cross(axis, v) * s + axis * dot(axis, v) * (1 - c);
}

The resulting vector from this direct translation of Rodrigues' formula into HLSL is exactly equal to the SG's Unity_RotateAboutAxis_Radians_float() function output.

Comparison of properties of both functions:

Reason

Since we as humans are not perfect, I believe every algorithm and calculation can be simplified even further and a quick internet search assured me this is just the case for SG's implementation. Notice they normalize the axis vector for you, something which will trigger unnecessary re-normalization if you're like me who always keeps such vectors normalized even before a call to such function.

Remarks

When inspecting the FXC compiled shader I noticed it has been reduced from 20 instructions for SG's function to just 10 instructions using Rodrigues' function. But as you can see from the comparison table above, half FXC reduction doesn't always equal half reduction in the actual ISA assembly.

Fresnel Effect

Fresnel Effect node is very useful when you're dealing with many types of materials where you either don't remember the fresnel equation or you just want to simplify your workflow. What I found about its code surprised me and will probably you as well.

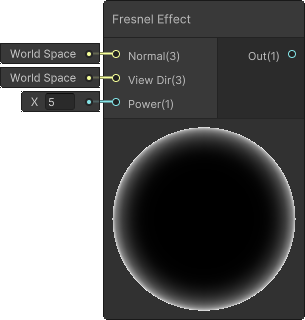
Generated code from SG:

void Unity_FresnelEffect_float(float3 Normal, float3 ViewDir, float Power, out float Out)
{
    Out = pow((1.0 - saturate(dot(normalize(Normal), normalize(ViewDir)))), Power);
}

And its ISA disassembly:

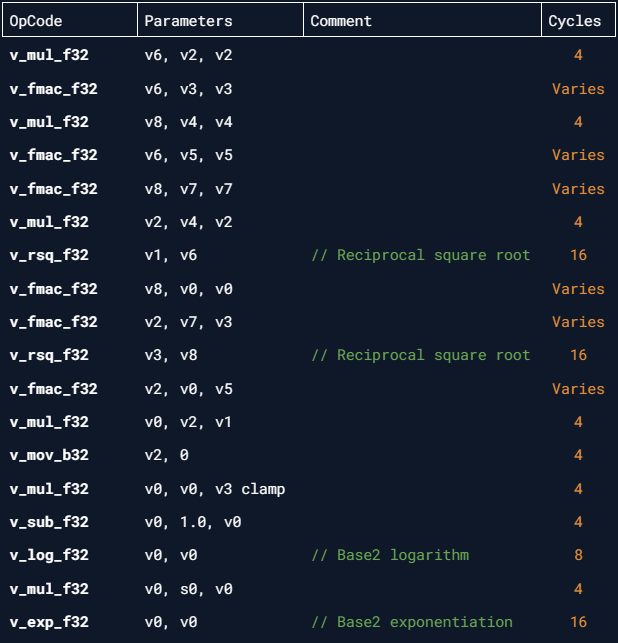
Quite long isn't it? The ISA execution will cost at least 88 clock cycles because it has to normalize both Normal and ViewDir vectors.

I decided to remove the normalization part and here is the final HLSL:

float Fresnel(float3 normal, float3 viewDir, float power)
{
    return pow(1 - saturate(dot(normal, viewDir)), power);
}

With its new ISA disassembly:

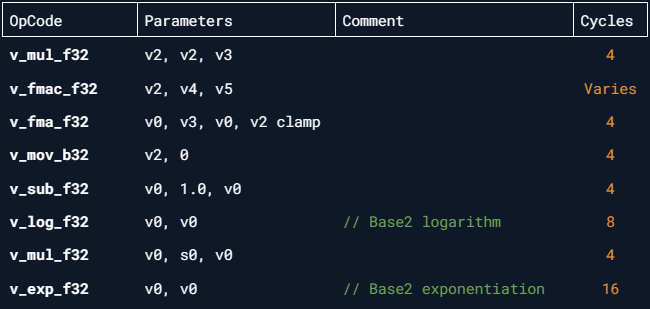
Now it shows us the amount of clock cycles has decreased by half to at least 44.

Reason

This is just my subjective opinion but every time I deal with normals, view direction or any other vector whose convention is to be always normalized I make sure to normalize them only once as soon as I obtain them. This way I know I don't have to re-normalize them again later in the shader, hence I removed the two redundant normalize() calls.

Of course, your opinion might differ so just keep in mind the Fresnel Node will normalize its input vectors every time which could be costly.

Remarks

Vector normalization is an expensive operation since it includes reciprocal square roots:

$$\displaylines{x_{norm} = {x \over{\sqrt{x^2+y^2}}} \\\\ y_{norm} = {y \over{\sqrt{x^2+y^2}}}}$$

And logically, the more components a vector has, the more calculations have to be done. The following HLSL code represents such normalization function:

float3 Normalize(float3 vect)
{
    return rsqrt(dot(vect, vect)) * vect;
}

For curious ones, the ISA breakdown of this function shows me it costs at least 32 clock cycles to compute. Of course that isn't much for a few vectors but can quickly add up if not careful.

Posterize

Usage of the Posterize Node might not be as common but I still wanted to show you how Unity team sometimes give unnecessary code to the GPU for execution.

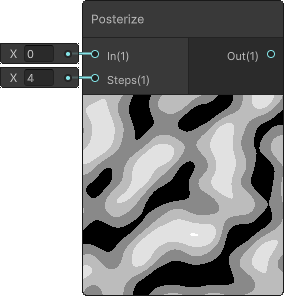
This is what SG generates:

void Unity_Posterize_float(float In, float Steps, out float Out)
{
    Out = floor(In / (1 / Steps)) * (1 / Steps);
}

I'm sure you can see the redundancy here. The ISA disassembly be like:

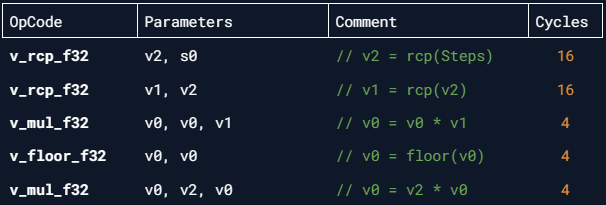
This shows us RGA decided to use two v_rcp_f32 calls, one of which is redundant. After simplifying this mess:

float Posterize(float value, float steps)
{
    return floor(value * steps) / steps;
}

Simplified ISA disassembly:

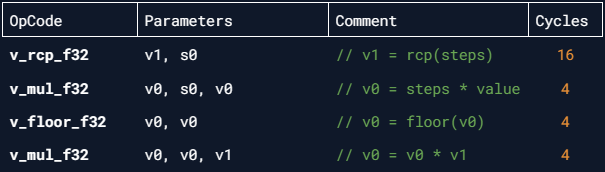
Just four instructions and only 1 v_rcp_f32. Of course, other GPU architectures might actually use division instruction so if that's bothering your performance you could use HLSL's rcp() (and half if on mobile):

half Posterize(half in, half steps)
{
    return floor(in * steps) * rcp(steps);
}

Reason

I really don't know why or how these obvious things slip into the production code but here's a quick explanation:

$${\left \lfloor in \over{1 \over steps} \right \rfloor} * {1 \over steps} = {{\left \lfloor in * steps \right \rfloor} \over steps}$$

Checkerboard

I view the Checkerboard Node as a useful visual debugging tool so I'm not as concerned with its efficiency but I am sure some developers use this node in production too. That's why I want to share my findings.

void Unity_Checkerboard_float(float2 UV, float3 ColorA, float3 ColorB, float2 Frequency, out float3 Out)
{
#if defined(SHADER_STAGE_RAY_TRACING)
    int2 checker = frac(Frequency * UV) > 0.5;
    Out = checker.x ^ checker.y ? ColorA : ColorB;
#else
    UV = (UV.xy + 0.5) * Frequency;
    float2 distance3 = 4.0 * abs(frac(UV + 0.25) - 0.5) - 1.0;
    float4 derivatives = float4(ddx(UV), ddy(UV));
    float2 duv_length = sqrt(float2(dot(derivatives.xz, derivatives.xz), dot(derivatives.yw, derivatives.yw)));
    float2 scale = 0.35 / duv_length.xy;
    float freqLimiter = sqrt(clamp(1.1f - max(duv_length.x, duv_length.y), 0.0, 1.0));
    float2 vector_alpha = clamp(distance3 * scale.xy, -1.0, 1.0);
    float alpha = saturate(0.5f + 0.5f * vector_alpha.x * vector_alpha.y * freqLimiter);
    Out = lerp(ColorA, ColorB, alpha.xxx);
#endif
}

The #if and #else preprocessor directives tell us that as long as the raytracing is not enabled (SHADER_STAGE_RAY_TRACING keyword is undefined) the GPU has to execute quite a lot of code for such a simple effect.

So can we simplify this?

All that is really necessary for such a checkerboard pattern is to use XOR logical operator. The code snippet from raytracing preprocessor block already implements such logic:

float3 Checkerboard(float2 uv, float3 colorA, float3 colorB, float2 frequency)
{
    uint2 checkerUV = frac(uv * frequency) > 0.5;
    return (checkerUV.x ^ checkerUV.y) ? colorA : colorB;
}

Here's the ISA breakdown comparison between both functions:

Reason

The checkerboard pattern is simple in a sense that one can imagine XOR's logical gate truth table output visualized on a 2x2 pixel grid. When output value == 0, draw a black pixel, otherwise draw a white pixel.

Remap

Although a Remap Node is written effectively I still wanted to show you how complicated formula at first is actually pretty simple one.

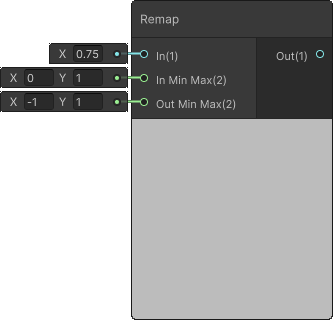
void Unity_Remap_float(float In, float2 InMinMax, float2 OutMinMax, out float Out)
{
    Out = OutMinMax.x + (In - InMinMax.x) * (OutMinMax.y - OutMinMax.x) / (InMinMax.y - InMinMax.x);
}

ISA disassembly:

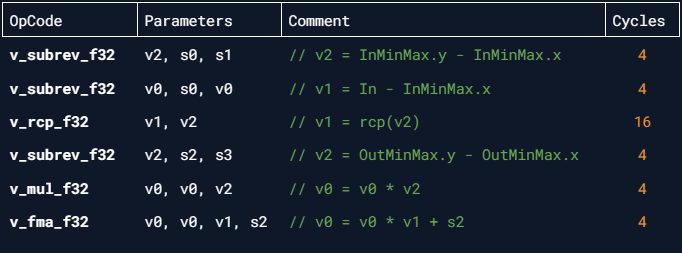
This formula is a pretty standard way of remapping values but could it be written to be more readable?

float Remap(float value, float2 inMinMax, float2 outMinMax)
{
    float normalizedValue = (value - inMinMax.x) / (inMinMax.y - inMinMax.x);
    return lerp(outMinMax.x, outMinMax.y, normalizedValue);
}

This code change reduces the instruction count for Remap from 6 to 5 which is a tiny gain but readability has increased much more.

Reason

From the second code snippet it is clear what remap actually does:

1. Use inverse linear interpolation to find normalized value from the input range.

2. Use linear interpolation to remap normalized value to the output range.

External Links

• How to read shader assembly by Kostas Anagnostou (2021)

• Shader Playground by Tim Jones (2018)

Thank you for reading!

Like what you see? If you found my facts about ShaderGraph helpful and want to show your appreciation, consider buying me a coffee on Ko-Fi. Your support helps me create more content like this!