Understanding Transformer Models - Part 1| The Self Attention Mechanism
 Parv Pareek
Parv Pareek
Introduction
In a world where cutting-edge technologies like ChatGPT, Bard, and DALL-E are making waves, you might be wondering how these technologies work. The enginge propelling these innovations is the revolutionary (In Optimus Prime voice)Transformer model. Tansformers have directly or indirectly changed everyone's lives in a way that it's influence is undeniable. It first proposed in the paper Attention Is All You Need [Vaswani et. al] by a team of researchers at Google Brain. It was initially introduced for language translation but no one knew about it's immense potential. Today we are going to discuss Self Attention, the backbone of the Transformer model.
Self Attention
The English language has words whose meanings change according to their surrounding context—bear, bank, bat, fair, lie, minute, and others. The term "bank," for instance, can denote a financial institution or a stretch of land sloping alongside a river, dependent on its contextual usage. But how does one equip a computer to decipher the nuanced meanings of millions of words present in the english vocabulary? This is where self attention comes in. Self attention is a mechanism that weighs neighboring words to enhance the meaning of the word of interest.During training, the self-attention mechanism allows the model to learn the contextual relationships and dependencies within the data, making it capable of producing accurate predictions.
Deconstructing the Self-Attention Process
Imagine the sentence "I swam across the river to get to the other bank." Humans intuitively discern that "bank" here signifies a riverbank. Conversely, the self-attention mechanism undertakes a multistep journey to unravel sentence meaning.
Step 1: Tokenization
The sentence is partitioned into individual words(called tokens)via a proecess known as tokenization. In the given sentence "I swam across the river to get to the other bank.", there are 11 tokens.
Step 2: Vectorization
Neural Networks don't possess the ability to understand words; they understand numbers. Therefore, each token undergoes a transformation into a vector representation, a process known as vectorization, often accomplished using algorithms like Word2Vec. These algorithms engineer vectors so that words that share a relationship or have a similar meaning are represented as neighboring vectors. Let's take a look at an Example
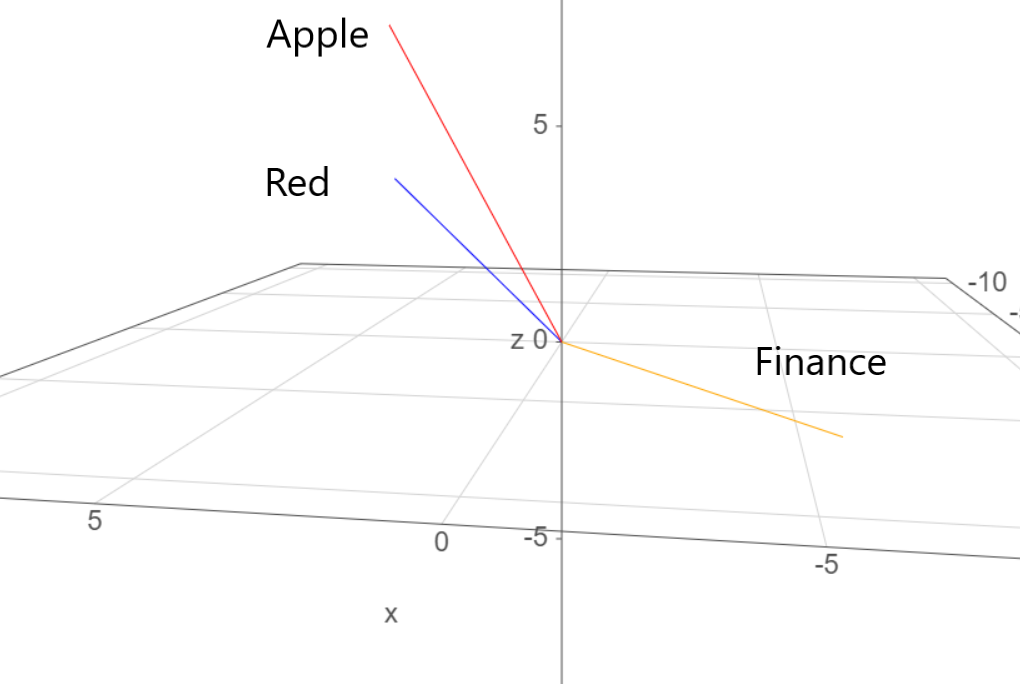
Consider this analogy: "Apple" and "red" coexist frequently, which reflects in their vectors, unlike "finance" that rarely associates with either. To visualize this phenomenon, we can refer to the word2vec mapping within the Tensorflow Projector.
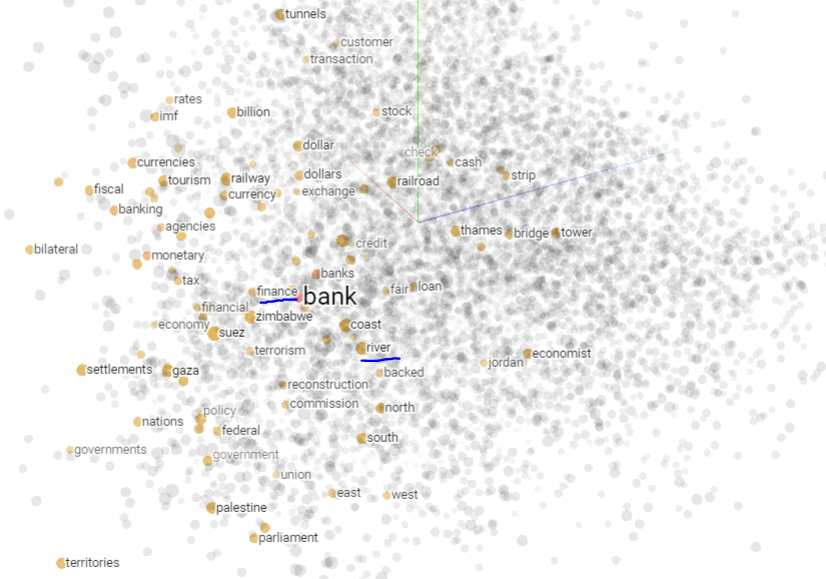
This tool shows vectors of the 100 closest neighbors to words like "bank," exposing correlations with "finance," "monetary," "tax," alongside "canal," "river," and "coast." Play around with it at https://projector.tensorflow.org/.
Step 3: Attention Scores
So far we can visualize our progress as such. We split the sentence into individual tokens and converted each token into a vector(1d matrix).

Attention scores quantify the "closeness" of words within a sentence. These scores are computed for every word in the sentence. Calculating these scores employs the concept of the dot product, a notion from linear algebra. The dot product between two vectors results in a singular number: higher values signify greater "closeness" between vectors. To calculate an attention score for a specific word(a.k.a the query) its dot product with every word in the sentence(the key) is evaluated. For a given query dot product is calculated for every possible pair in the sentence.
These scores then are passed through a nonlinear Softmax function, which normalizes them, giving us weights(which can also be called coefficients) that represent the importance of each word in the sentence with respect to a specific query. For example for the query "bank", the weights for the words "river" and "swam" will be higher compared to the other words in the sentence because the weights are generated by calculating the dot product of the vectors of each word with "bank"(in this example) and dot product is higher for vectors that are closer to each other. This process will "weigh" the words "swam" and "river" to be more significant with respect to bank.

The heatmap is a representation of the attention scores when dot product is calculated for words. Notice how the diagonal is completely white which means the score are really high because they are the same words. Notice the dark spots and how the two corresponding words are not all that related. The first row represents attention scores for the first word "I" with respect to each of the words in the sentence.
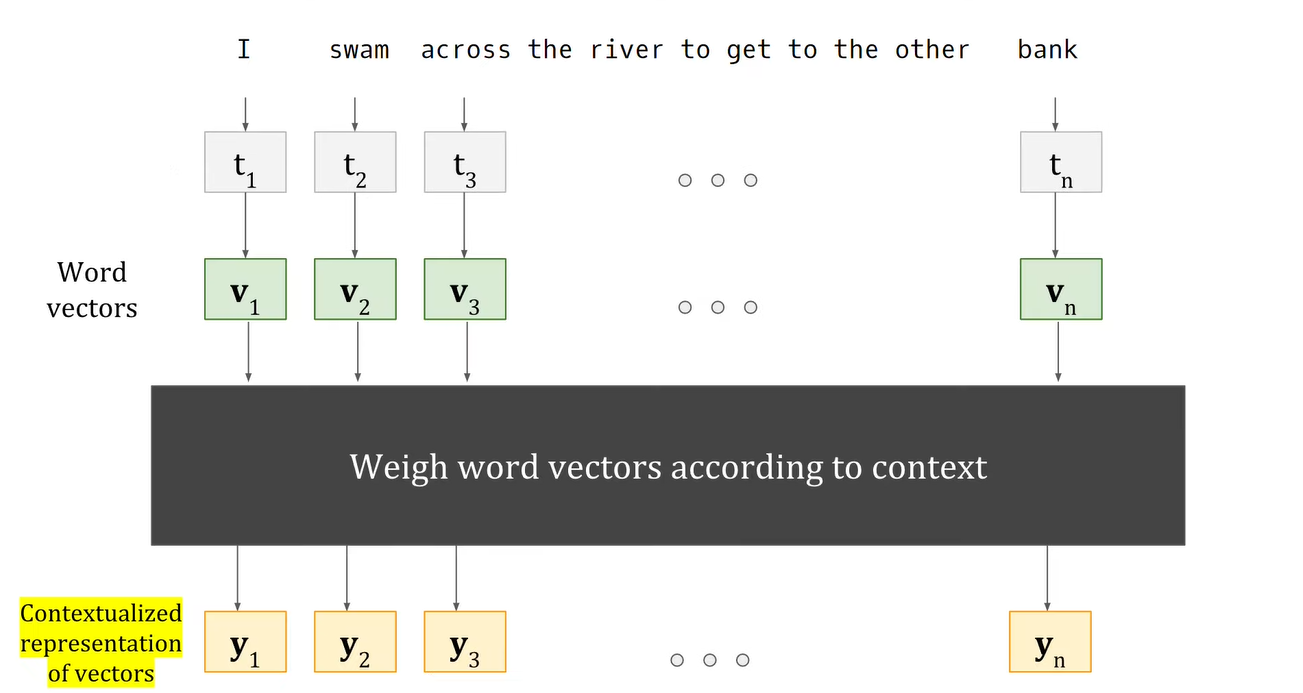
Step 4: Contextualized Representations
Now that we possess the assigned weights for each word, let's dive into how these weights give the context in relation to a specific word. To illustrate, consider the term "bank" from the sentence "I swam across the river to get to the other bank". The vectorized representations of the sentence's words (referred to as keys) will be labeled as v1, v2, v3... v11, corresponding to the 11 words present.
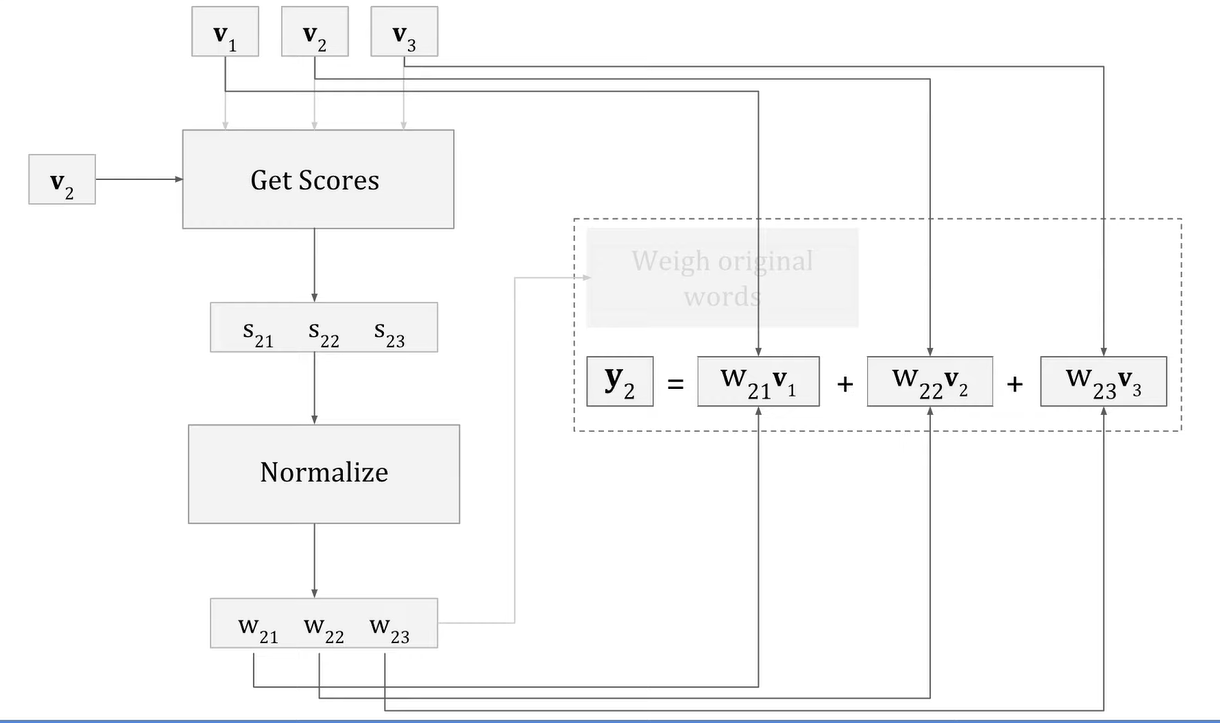
The concept of a contextualized word representation is fundamentally a vector. This vector encapsulates the comprehension of the context in which the word is present. In the original paper, this contextualized representation is also called as "Value" and going forward we will denote it as such. Each word maintains its individual contextualized representation: y1, y2, y3, y4... yn. To elaborate, let's consider the value for the initial word "I":
$$\begin{align*} y_1 &= w_{11}v_1 + w_{12}v_2 + w_{3}v_3 + \ldots + w_{111}v_{11} \\ y_2 &= w_{21}v_1 + w_{22}v_2 + w_{23}v_3 + \ldots + w_{211}v_{11} \\ \end{align*}$$
This y1 vector contains all the context between I and the rest of the words
Here, W1n captures the nuanced relationship between the first word and the nth word. It's imperative to recall that the dot product elevates for words that frequently co-occur, such as "apple" and "red." Extending this principle, the value assigned to the word "bank" becomes:
$$y_{11} = w_{111}v_1 + w_{112}v_2 + w_{113}v_3 + \ldots + w_{1111}v_{11}$$
From our knowledge we can conclude that the weights for the words "river" and "swam" will be higher for the value of the word bank because they share relations. This contextualized representation tells the transformer which words to pay attention to and hence the name of the mechanism.
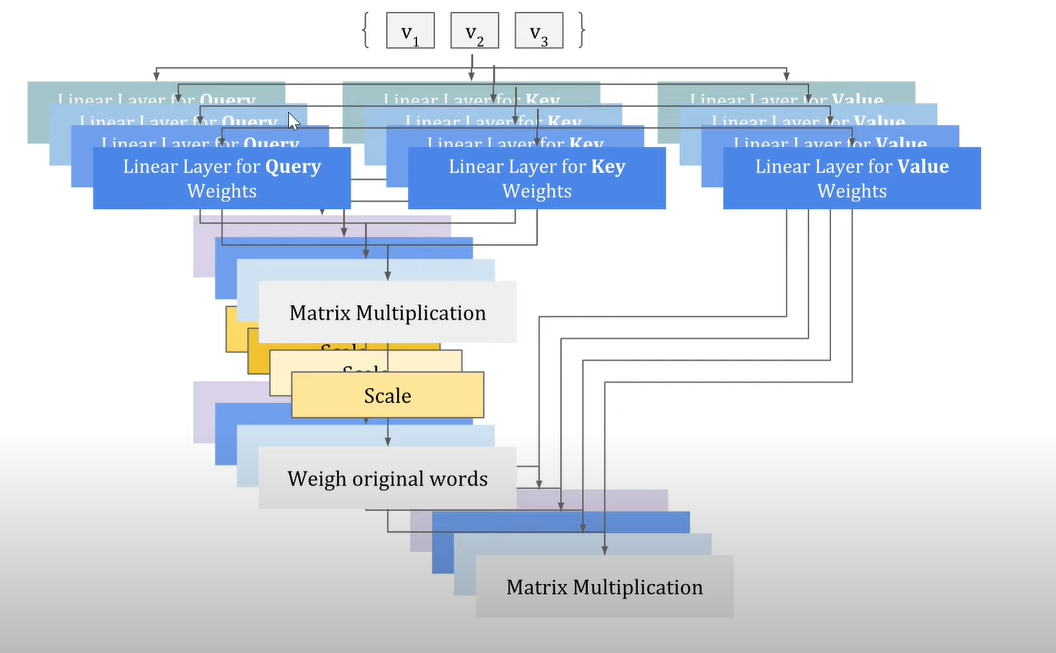
Step 5: Multi Head Attention
Multi-head attention is an extension of the self-attention mechanism used in transformer-based models, where the self-attention process is applied multiple times in parallel but with different sets of learned parameters. It enables the model to capture different types of relationships and dependencies within a sequence, enhancing its ability to extract and incorporate relevant information.
Conclusion
Armed with a mathematical grasp of the revolutionary transformer model's fundamental, the self-attention mechanism I've unveiled its potential. In a forthcoming article, I'll discuss about the Encoder's utilization of self-attention and delve into various encoder-based transformers, such as the renowned BERT model.
Subscribe to my newsletter
Read articles from Parv Pareek directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
