Understanding Lasso Regression

Lasso regression, short for Least Absolute Shrinkage and Selection Operator Regression, is a supervised learning model that uses the L1-Regularization technique to reduce the overfitting of the model. Well, you will get to know what the abbreviations mean shortly.

Intuition

Lasso Regression is based on Linear Regression. Linear regression is a common method used to model the relationship between a dependent variable and one or more independent variables.

Linear Regression Equation: Y=w X + b,w and b are the weight and bias of the model.

Now, let's consider a situation where a linear model uses higher-degree polynomial equations. As we observe the image below, we can see that the 9th-order polynomial is overfitting the data, where X is an independent variable and Y is dependent on X.

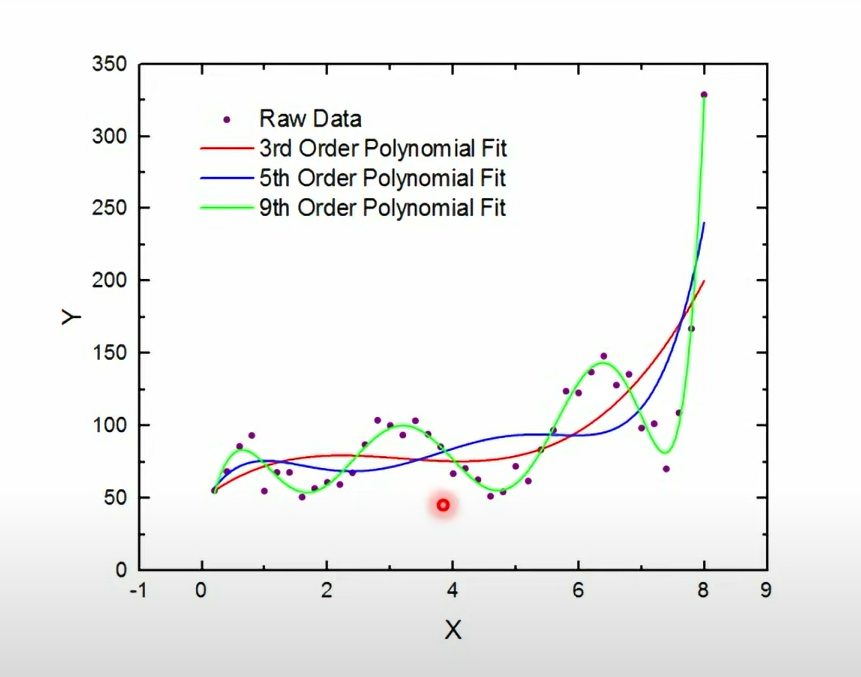
Overfitting is a common problem in ML models where the accuracy of the training data is very high, but the accuracy of the test data is low which leads to inaccurate predictions. As the complexity of the model increases, it tends to overfit within its data. If it is a simple model, there will be no problem of overfitting. This is where regularization comes into play.

Now let's see in the sense of Multiple Linear Regression, where the value of a dependent variable is predicted based on two or more independent variables which also tends to overfit the data because of high-dimensional data and multicollinearity (occurs when two or more independent variables are highly correlated).

Simple Linear Regression: Y= wX +b

Multiple Linear Regression:

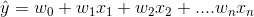
where (x1, x2, x3 ) are the dimensions/features of the data. Because of the more features the model tends to be overfit the data. So to reduce the overfitting of data, you need to use a regularization technique.

What is Regularization (λ)?

Regulation is used to reduce the overfitting of the model by adding a penalty term (λ) to the model.

• Lasso Regression uses the L1 regularization technique.

• By the introduction of a penalty term serves to diminish the significance of certain coefficients in a mathematical model, effectively reducing the impact of their influence. As a result, overfitting can be avoided. This process is known a Shrinkage.

• 

After introducing the penalty term (λ), the previously overfitted curve has transformed into a well-fitting one.

Feature Selection

Feature Selection encourages certain coefficients in a linear regression model to be exactly zero. This results in automatic feature selection, as the Lasso penalty aims to eliminate the impact of less important features by shrinking their corresponding coefficients to zero.

So Lasso, or Least Absolute Shrinkage and Selection Operator, achieves feature selection and shrinkage in linear regression by encouraging certain coefficients to become precisely zero based on a regularization parameter.