Dutch National Flag Algorithm
 Alisha Kausheen
Alisha Kausheen
Talking about Dutch National flag algorithm all we can think of is a problem , if and else conditions in loop and there we go the array is sorted.But we never talked about its intution , why we use and how it actually work. Lets dive into the algorithm.
Introduction
Dutch National Flag Algorithm revolves around sorted and unsorted parts of array i.e. expanding the sorted section and shrinking the unsorted section of that array.
Approach
- This is a 3-pointer approach algorithm
Taking 3-pointers named:
low
mid
high
(named them in this way so that it is easy to remember and recall)
Motive:
It will divide the array in a way like:
should contain all 0's--->extreme left
should contain all 1
should contain all 2's---->extreme right
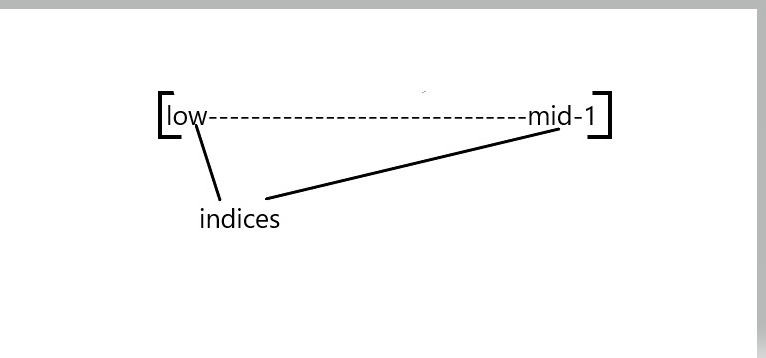
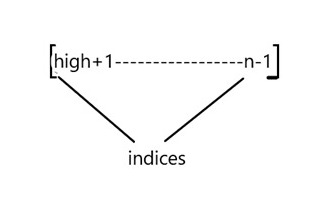
According to the Dutch National Flag Algorithm, array will somewhat look like:

We can see that from 0 index to mid-1 index and from high+1 to n-1 indices array is sorted and from mid to high array is unsorted
Now lets sort the unsorted section.
Remember in the beginning we talked about shrinking the unsorted section and expanding the sorted sectioh.
Its the right time to understand that:
Algorithm
Three steps:
Step1:
array[mid]==0
then swap(array[low],array[mid])
and low++,mid++
Step2:
array[mid]==1
then mid++
Step3:
array[mid]==2
then swap{array[mid],array[high])
high--
{i.e. shrinking the portion between mid and high indices}
Intiution
To understand whats behind all this arrangement and taki8ng 3-pointers lets take the famous 0's 1's 2's sorting problem
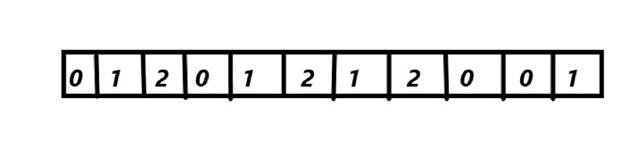
Problem:
Sort an array 0's 1's 2's
Using Dutch National Flag Algorithm:
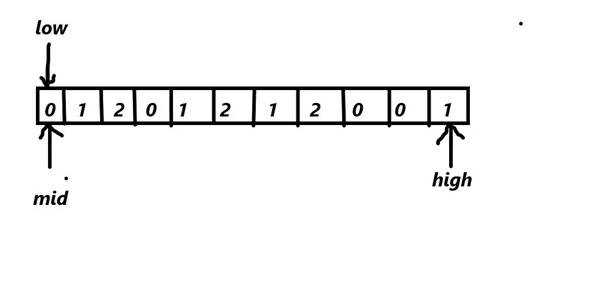
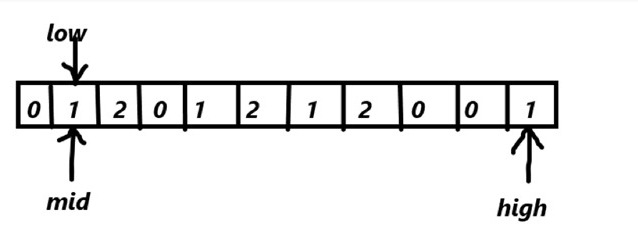
As the whole array is umsorted
mid=0
low= 0
high=n-1
where n= length of the array
array[mid]==0
so mid++, low++
swapping array[mid]=array[low] wont makes sense as low = mid
array[mid]==1
mid++
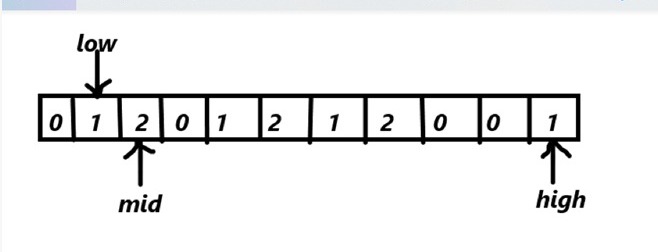
array[mid]==2
swap(array[mid],array[high])
high--
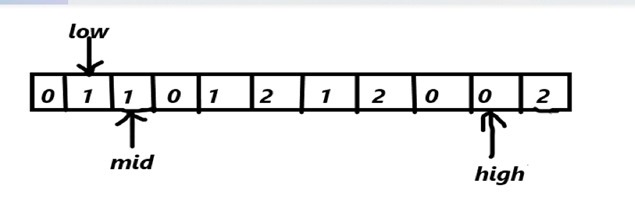
array[mid]=1
mid++
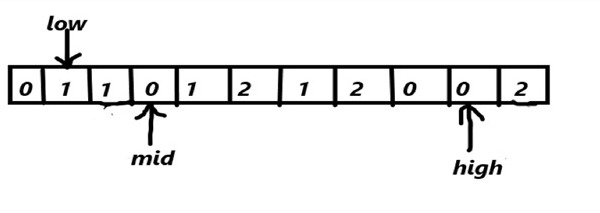
array[mid]==0
swap(array[mid],array[low])
mid++
low++
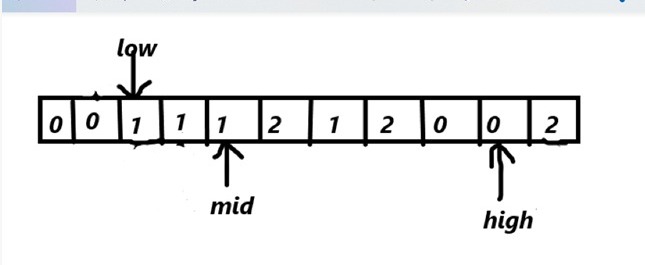
array[mid]==1
mid++
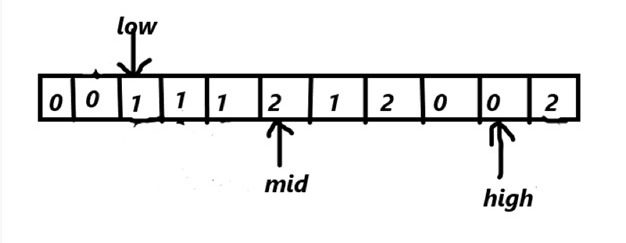
array[mid]==2
swap(array[mid],array[high])
high--
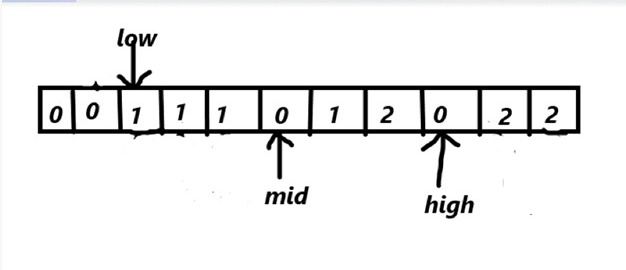
array[mid]==0
swap(array[mid],array[low])
mid++
low++
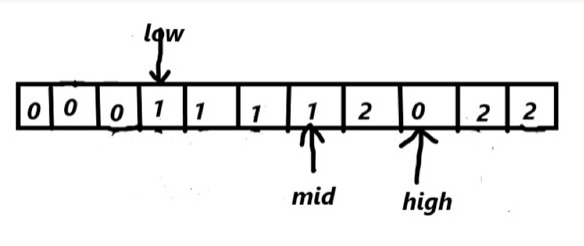
array[mid]==1
mid++
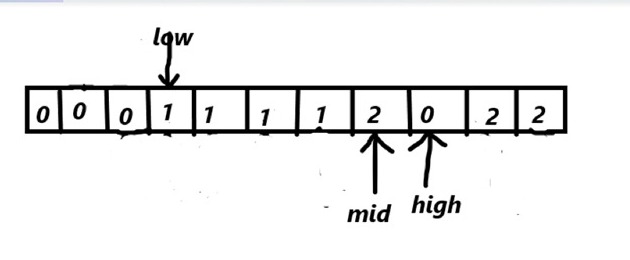
array[mid]==2
swap(array[mid],array[high])
high--
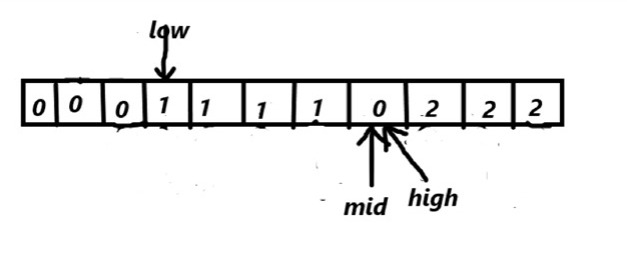
array[mid]==0
swap(array[mid],array[low])
mid++
low++
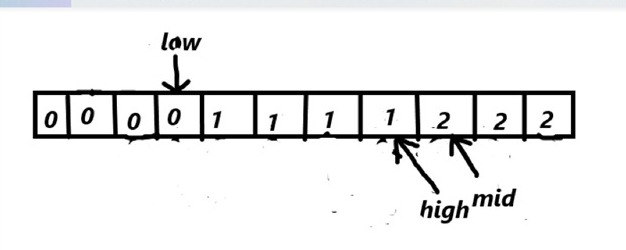
We can see that mid by-passed high pointer
that indicates the end of sorting and the array is sorted now.
Dry Code
int low=0,mid=0,high=n-1;
while(mid<=high)
{
if(array[mid]==0)
{
swap(array[low],array[mid]);
low++;
mid++;
}
else if(array[mid]==1)
{
mid++;
}
else{
swap(array[mid],array[high]);
high--;
}
}
Time Complexity: O(n)
Space Complexity:O(1)
Subscribe to my newsletter
Read articles from Alisha Kausheen directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by