Nonlinear Finite Element Analysis (FEA)

Finite Element Analysis (FEA) is a powerful tool for solving complex problems in various engineering fields. One of its more advanced applications is nonlinear FEA, which is designed to address issues that don't conform to linear behavior. In this blog post, we'll break down the basics of nonlinear FEA and walk through some examples to help its principles.

What is Nonlinear FEA?

In engineering, many systems exhibit linear behavior under certain conditions, meaning their response is directly proportional to the input or load. However, when materials, geometric conditions, or boundary conditions deviate from this linearity, nonlinear FEA is necessary.

Nonlinear FEA can be categorized into three primary types:

1. Material Nonlinearity: When materials no longer obey Hooke's law (i.e., stress is no longer proportional to strain). Examples include plastic deformation in metals or hyperelastic behavior in rubbers.

   

2. Geometric Nonlinearity: Often called "large deformation" or "large displacement" analysis. It occurs when the deformation of the structure changes its original geometry substantially.

   

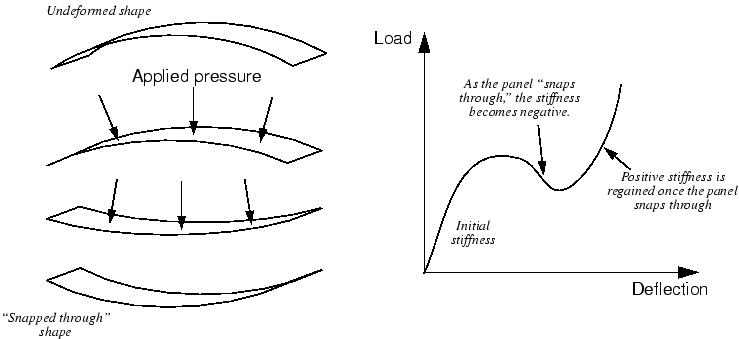
3. Boundary Nonlinearity: This involves changing boundary conditions, such as contact between components.

Why Use Nonlinear FEA?

Linear FEA is faster and requires fewer computational resources. However, nonlinear FEA becomes necessary when:

• Predicting the failure of a component or structure.

• Designing materials that undergo large deformations.

• Analyzing structures with complex contact interactions.

Examples

Example 1: Rubber Seal Analysis (Material Nonlinearity)

Consider a rubber seal placed between two rigid bodies. As the bodies are pressed together, the seal undergoes large elastic deformations. Using a hyperelastic material model for the rubber, nonlinear FEA can predict the stress distribution and the deformation of the seal under load.

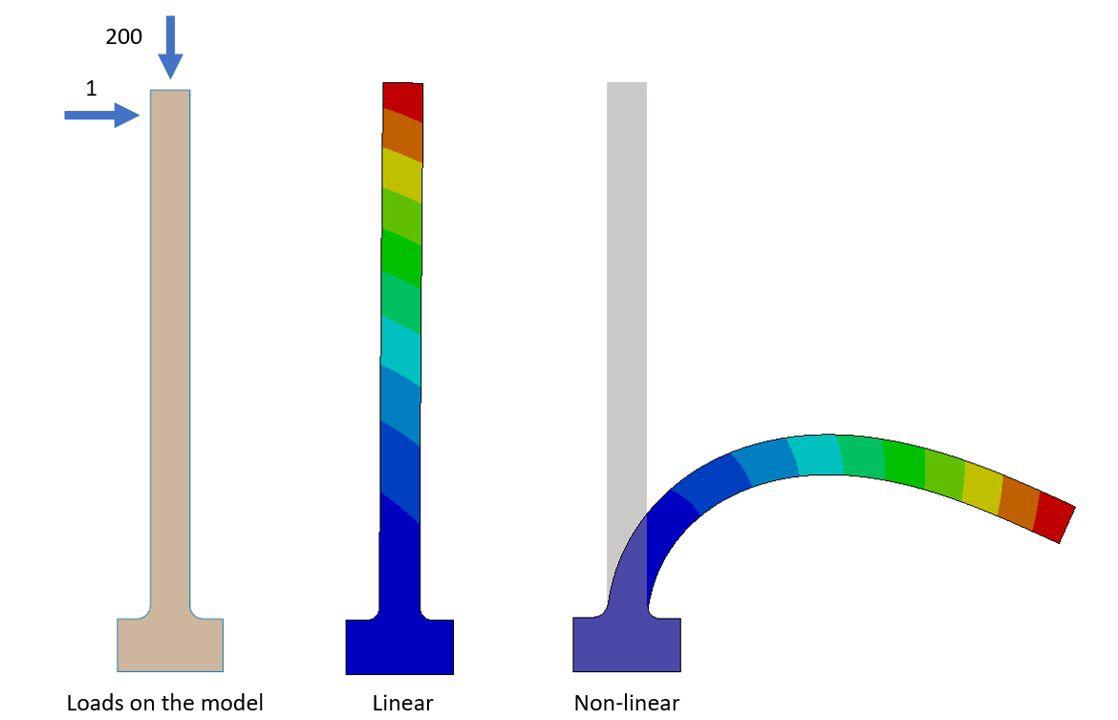
Example 2: Buckling of a Slender Column (Geometric Nonlinearity)

Imagine a slender column under compressive load. As the load increases, there's a point where the column suddenly buckles and deflects laterally. This behavior is inherently nonlinear and requires nonlinear FEA to predict the buckling load accurately.

Example 3: Gear Interaction (Boundary Nonlinearity)

For two interacting gears, as they rotate, different teeth come into contact, causing the boundary conditions to change. Nonlinear FEA, with a contact algorithm, is crucial to evaluate the stresses on the gear teeth accurately.

Challenges in Nonlinear FEA

• Convergence Issues: Due to the inherent complexity of nonlinear problems, solutions might not converge, especially if the problem is ill-posed or the mesh isn't adequate.

• Computational Cost: Nonlinear FEA requires iterative methods, making them more computationally intensive than linear simulations.

• Material Modeling: Accurate material models are critical, and sometimes experimental data is required to calibrate these models.

Best Practices

• Start Simple: Before diving into a full nonlinear analysis, begin with linear assumptions and then gradually introduce nonlinearity. This stepwise approach can help identify issues early on.

• Mesh Refinement: Nonlinear problems are sensitive to mesh quality. Start with a coarser mesh and refine in areas of interest or where higher accuracy is needed.

• Use Symmetry: If the geometry and loading conditions allow, use symmetry to reduce the size of the model and save computational time.

Conclusion

In simple terms, nonlinear FEA is like a detailed map for engineers. Even though it can be tricky to use, it's super helpful. It lets us see how things like rubber bands stretch or when a machine part might break. By using it, engineers can make better and safer designs.