What is Bloch Sphere of a Qubit?

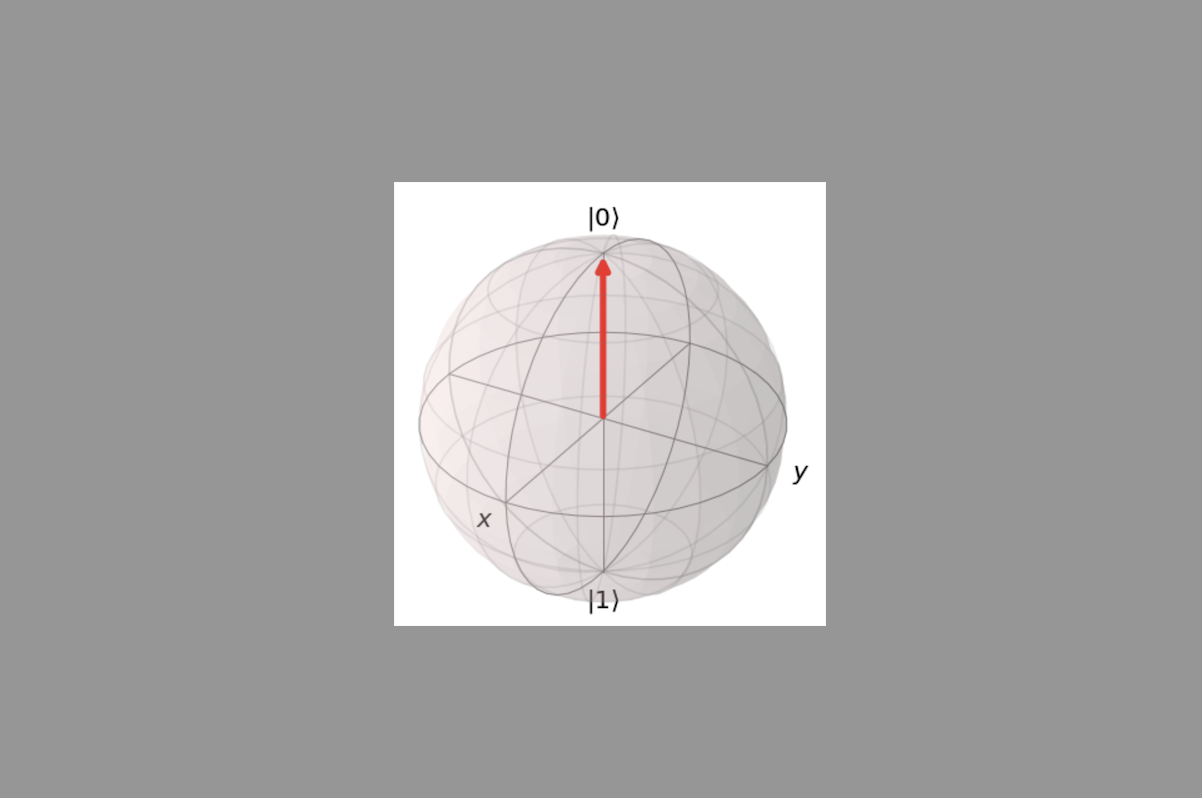
"Visual memory is the strongest memory! Let's visualize a qubit"

Index

• Mathematics and Representation of the Bloch Sphere

  • Relative and Global phases

• Different states on the Bloch Sphere

  • States on the Z-axis

  • States on the X-axis

  • States on the Y-axis

• Eigenstates of Pauli X, Pauli Y, Pauli Z matrix

  • Pauli-Z Gate

  • Pauli-X Gate

  • Pauli-Y Gate

• Inner Product

  • Z-axis Gate

  • X-axis Gate

  • Y-axis Gate

• Coordinates of states on the Bloch Sphere

  • States on the Z-axis

    • |0> state

    • |1> state

  • States on the X-axis

    • |+> state

    • |-> state

  • States on the Y-axis

    • |↺> state

    • |↻> state

• Rotations on Bloch Sphere and Trajectory

  • Right-Hand Thumb Rule

  • X-Gate

  • Y-Gate

  • Z-Gate

• Code Snippet for one of the traces on Bloch Sphere

• Conclusion

Mathematics and Representation of the Bloch Sphere:

In geometry, the equation of a circle in the X-Y coordinate plane is given by x = rcosθ and y = rsinθ. For a standard unit circle, r=1. Hence the equation of the standard unit circle is given by x=cosθ and y=sinθ. Now, the number of angles associated with the equation is one i.e. θ and the circle it represents is a 2-D circle. So if there are 'n' angles associated with an equation, it represents a geometric object of 'n+1' dimensions.

Now in quantum information theory, a valid quantum state is given by the equation :

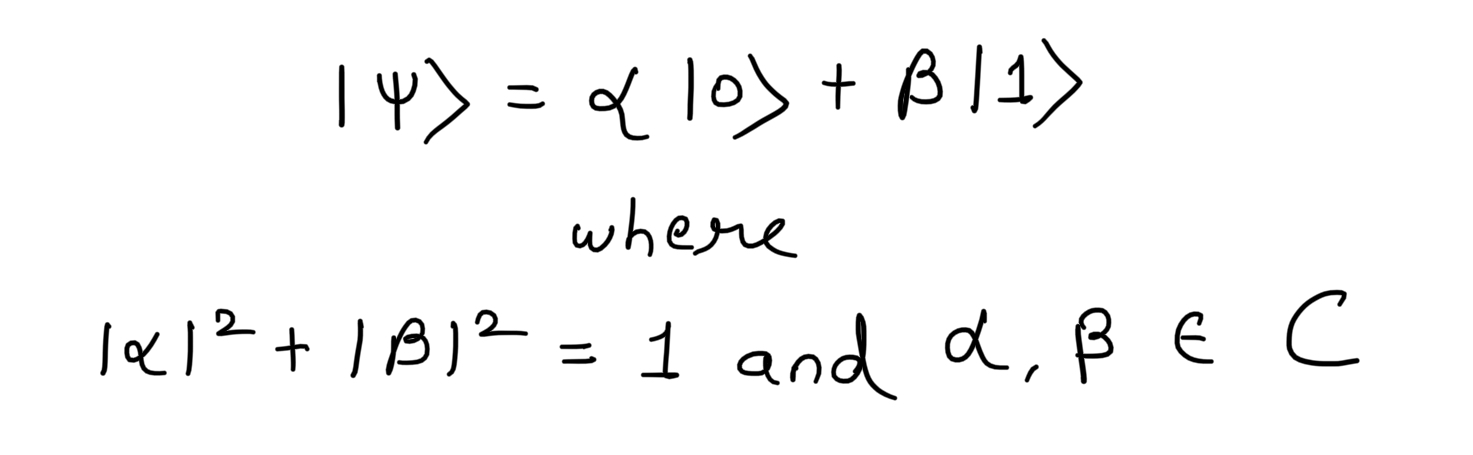
where 'C' is a set of Complex numbers.

Let's consider an angle 'Φ' which introduces a relative phase in the qubit state. A relative phase is the difference between the phases of the coefficients of |0> and |1>. E.g. |0>+|1> and |0>-|1> differ by a phase of Φ=Π. A relative phase is the core of quantum computing. If there are 2 quantum states with different relative phases(i.e. 2 values of Φ) then both the qubit states are different. Mathematically a qubit state with a relative phase is given as :

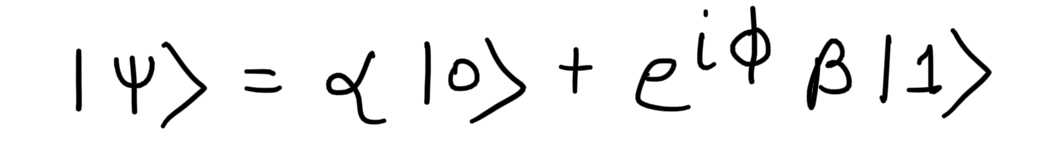
Let's consider an angle 'γ' which introduces a global phase in the qubit state. A global phase is a phase applied on coefficients of |0> and |1> both together. The global phase does not affect the quantum state i.e. a quantum state remains unchanged on application of a global phase. Mathematically a qubit state with a global phase is given as:

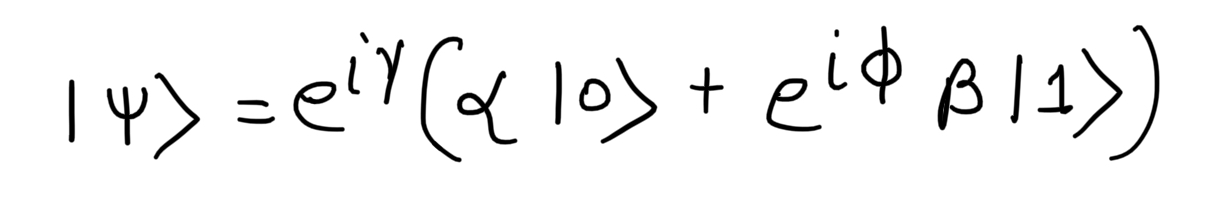
Consider an example to understand why the global phase does not affect the quantum state:

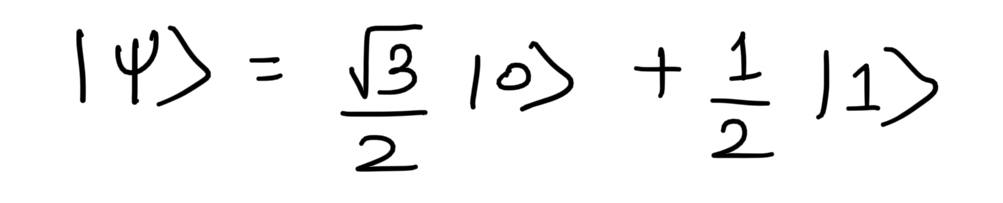
If we measure the quantum state on Z-basis then the probabilities are given as follows:

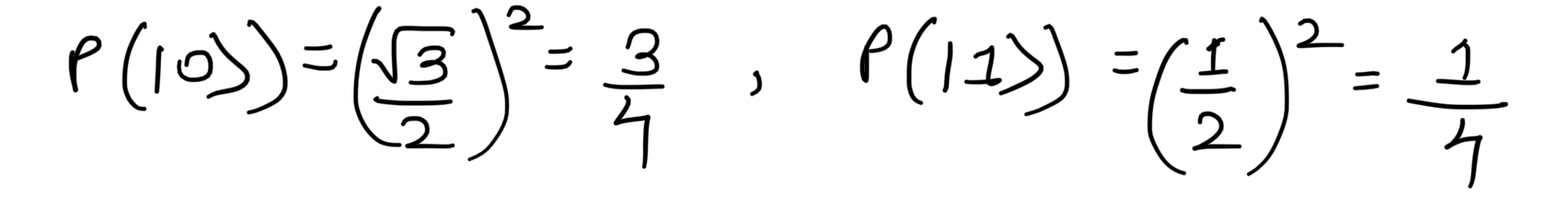
Let's introduce a global phase 'γ'

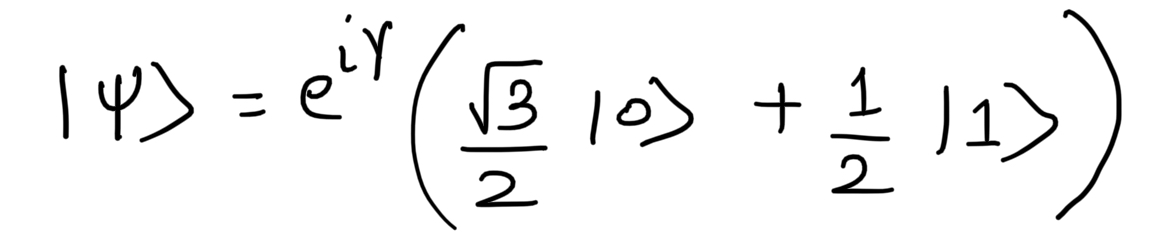
Now if we measure the above quantum state on a Z-basis then the probability of getting the state |0> is

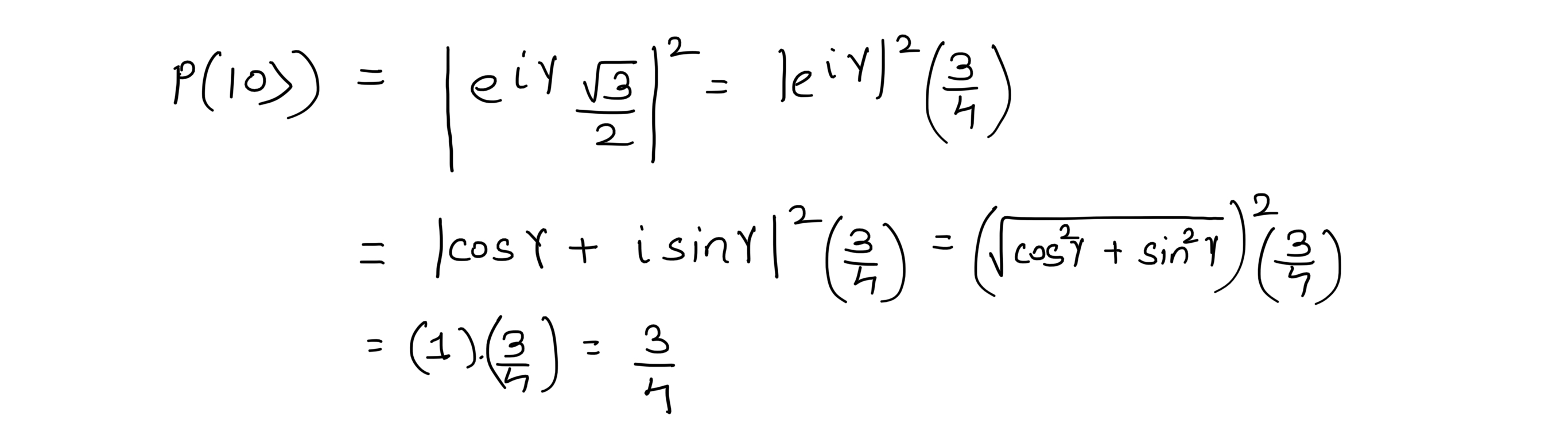
Also, the probability of getting the state |1> is

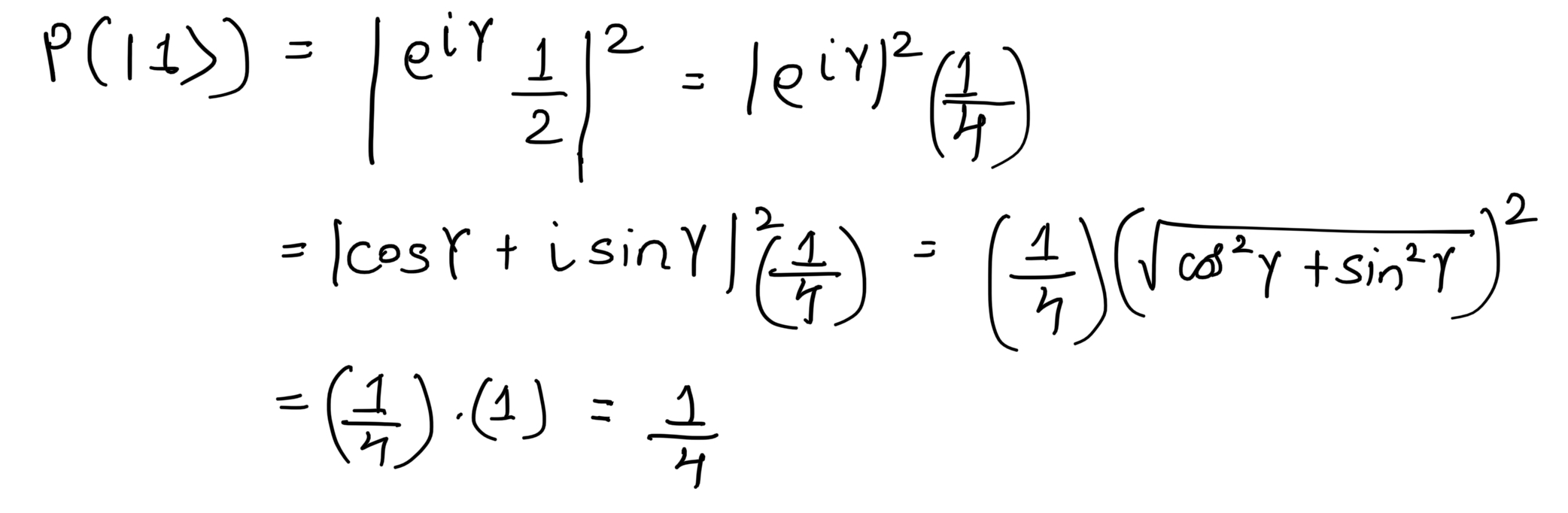
So the probability of getting state |0> or |1> is the same for both cases (with or without the global phase). Hence global phase does not affect a quantum state. Due to this, we will write our quantum state as

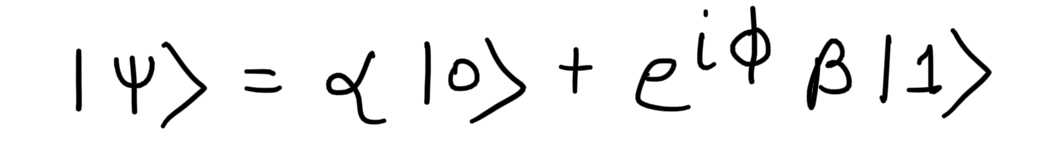
The amplitude of our quantum state must be 1 i.e.

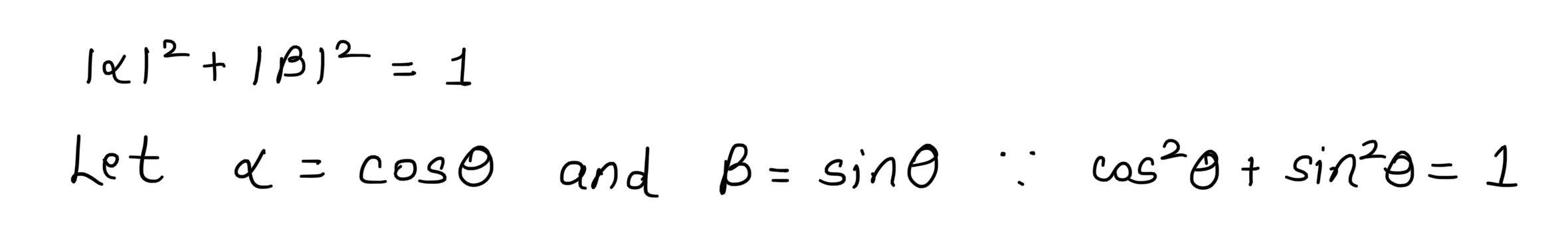
Hence, the final representation of a qubit is given as:

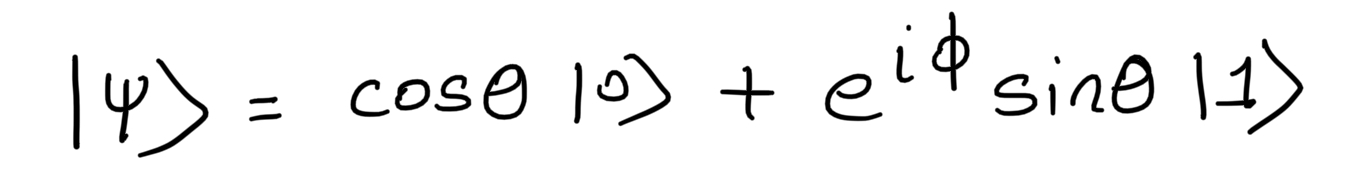
Here there are 2 angles θ and Φ. Hence the given equation can be represented in (2+1)=3 dimensional sphere. This sphere is called a Bloch Sphere. It is a visualization tool that maps the 2-D complex state vector onto a real 3-D space. This Bloch Sphere is defined in the Hilbert Space which is a geometrical space equipped with an inner product.

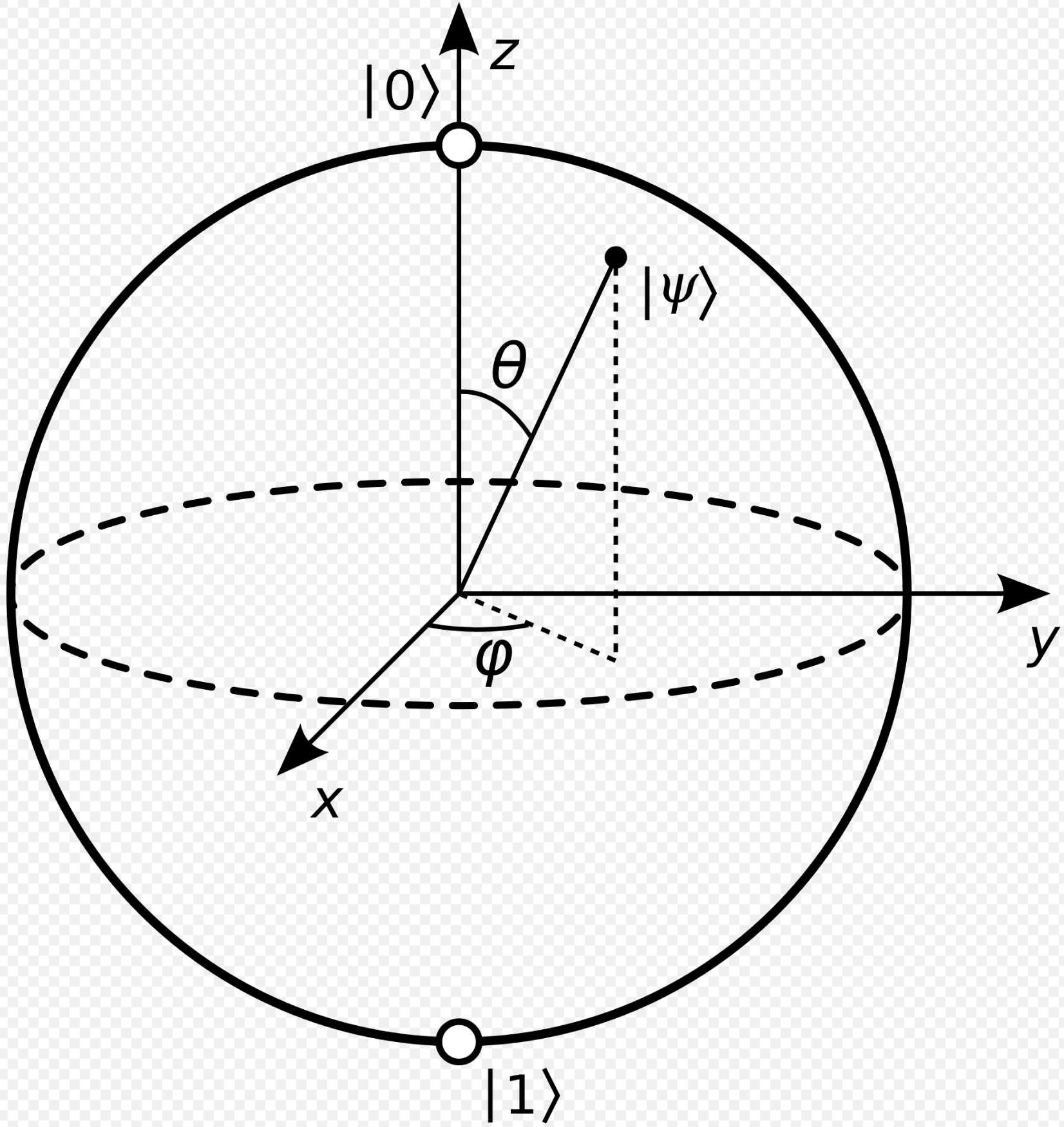
θ is the angle w.r.t. Z-axis and Φ is the angle w.r.t. X-axis. The antipodal points on a bloch sphere represent orthogonal vectors. Hence |0> and |1> are orthogonal vectors. The radius of the Bloch sphere is of length 1. Each point on the surface of the Bloch sphere is a unique Quantum state. Rotations on the Bloch sphere do not reduce the length of the vector.

Different states on the Bloch Sphere: There are 6 important states on the Bloch Sphere. 2 on the X-axis, 2 on the Z-axis and 2 on the Y-axis.

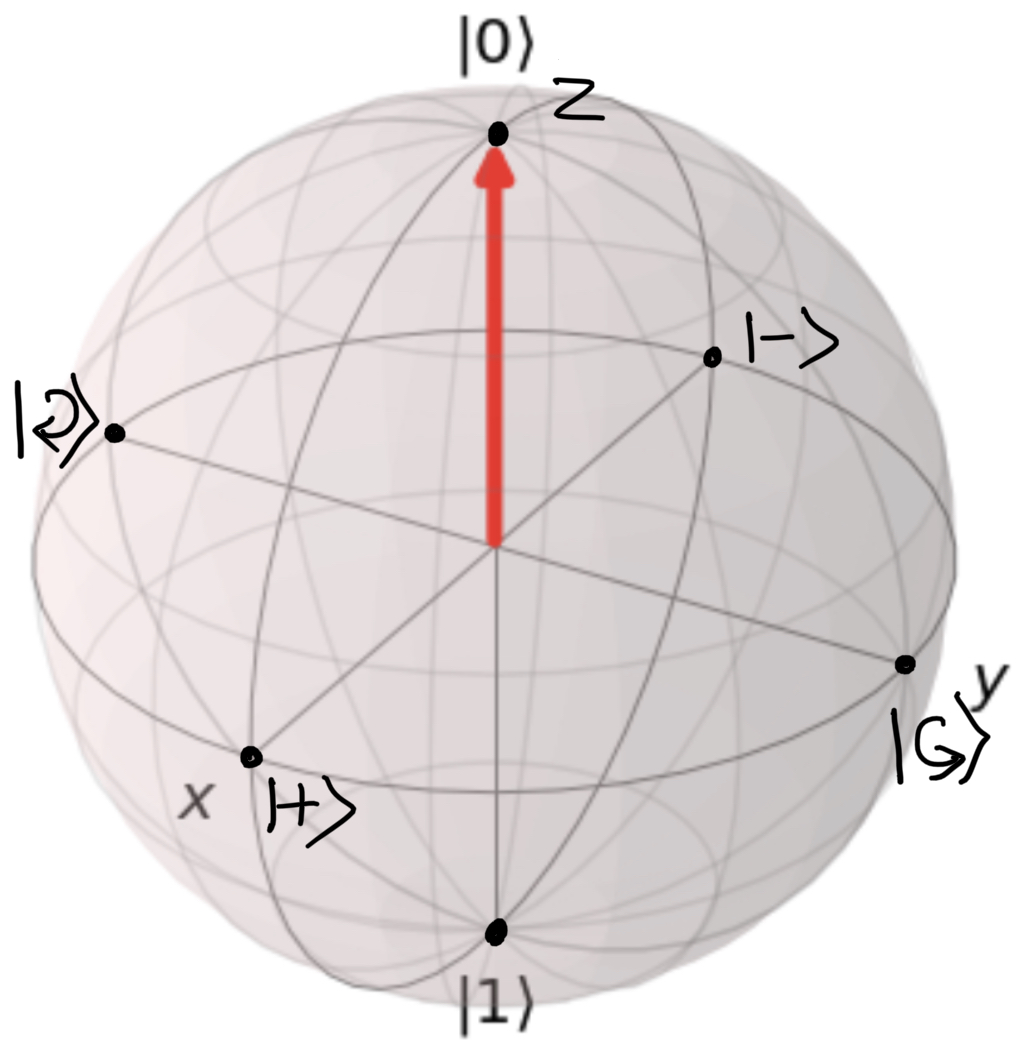
1. States in the Z-axis:

   

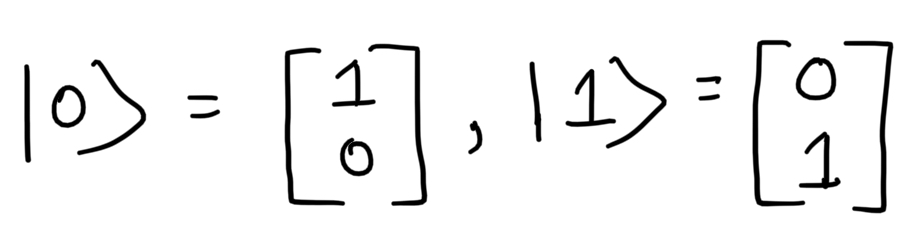
2. States in the X-axis:

   

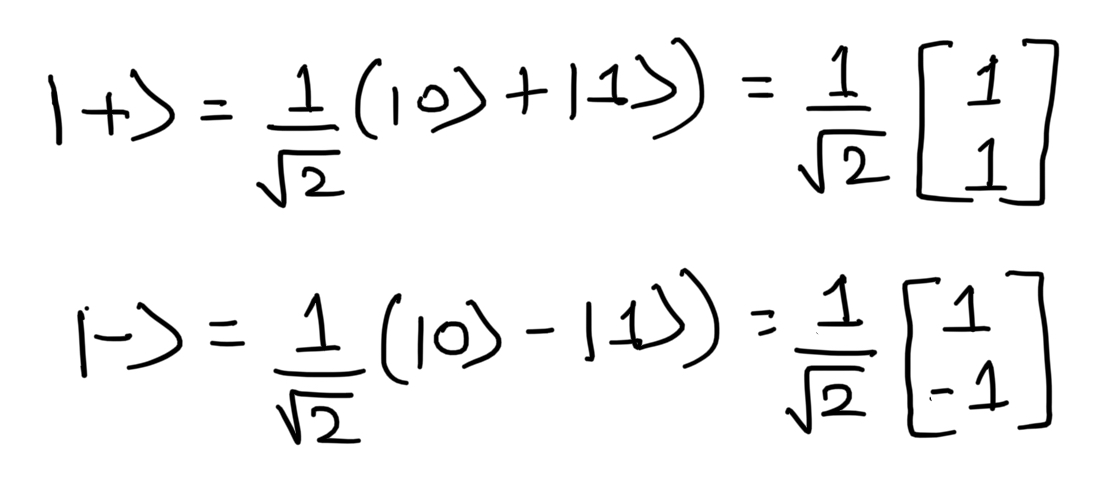
3. States in the Y-axis:

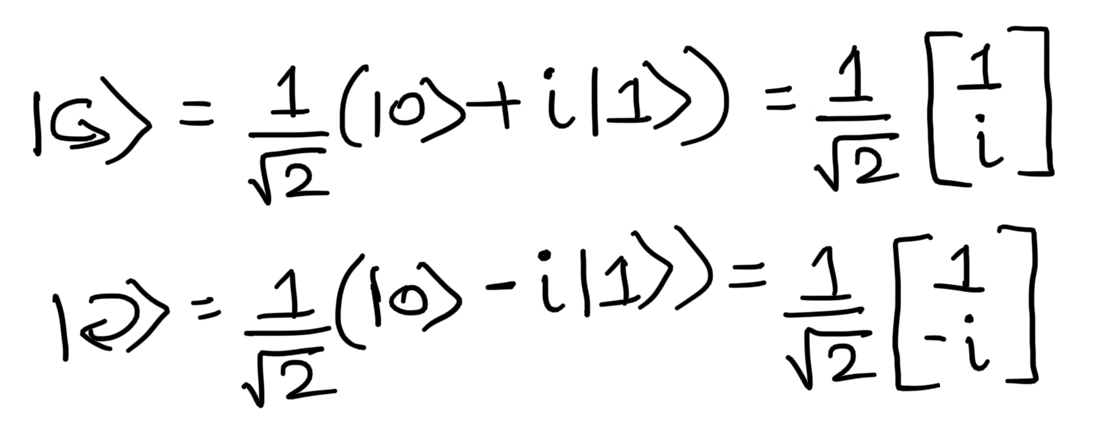
Eigenstates of Pauli X, Pauli Y, Pauli Z matrix:

If 'A' is a square matrix, 'x' is the eigenvector of 'A' and 'λ' is the eigenvalue of 'A' then Ax = λx.

1. Pauli-Z Gate

   Consider the Z-Gate matrix.

   

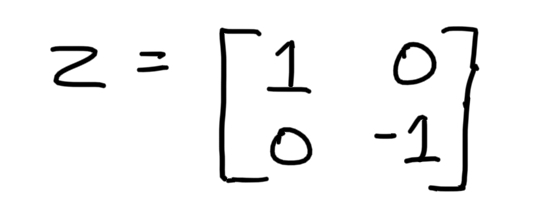
   Consider the states on the Z-axis.

   

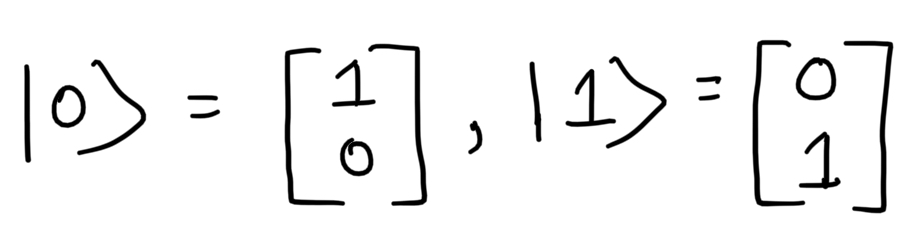
   Now let's check the equation for the eigenvalue and eigenvector.

   

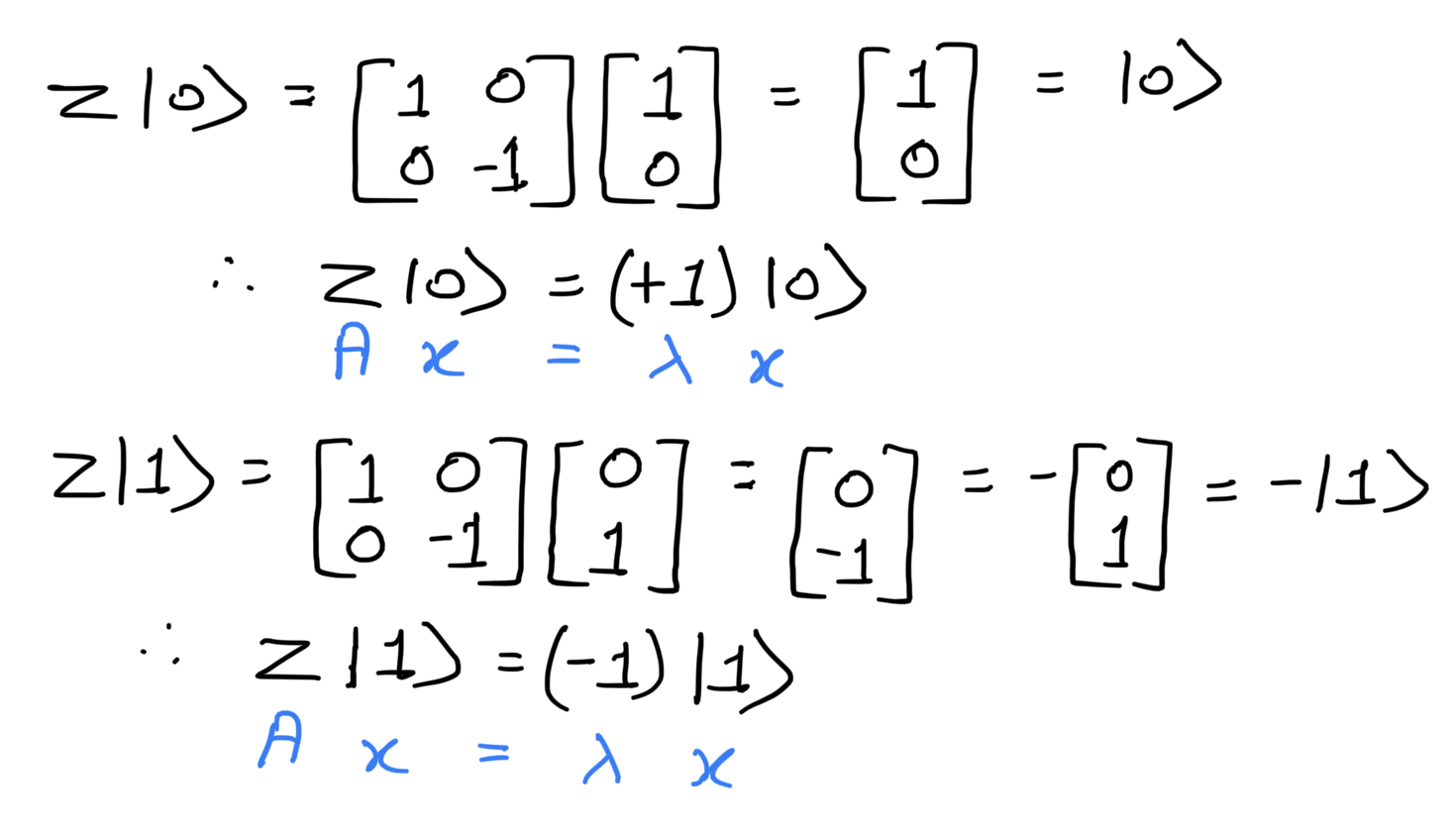
   Hence +1 and -1 are the eigenvalues and |0> and |1> are the eigenvectors of the Pauli-Z matrix.

2. Pauli-X Gate

   Consider the X-Gate matrix.

   

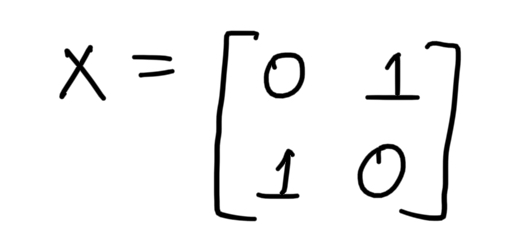
   Consider the states on the X-axis.

   

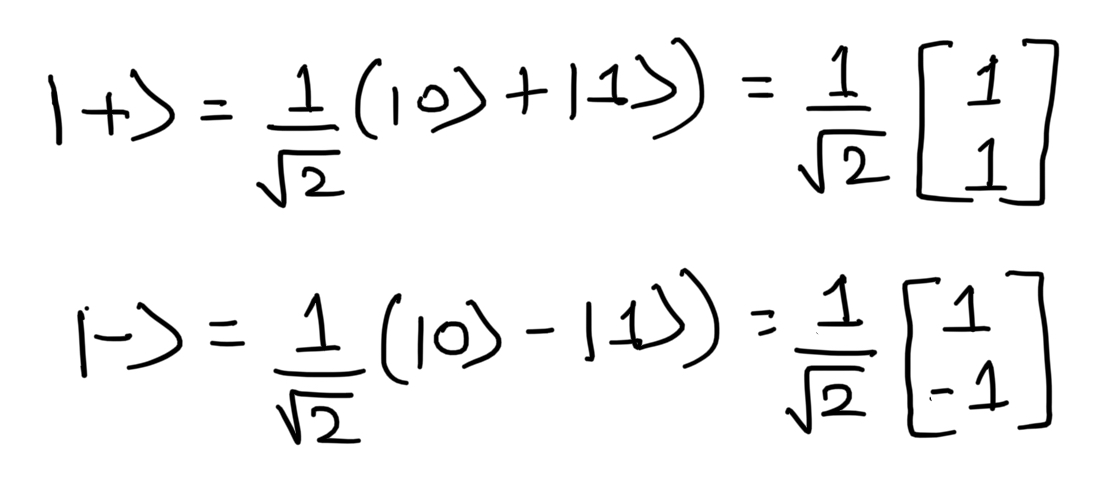
   Now let's check the equation for the eigenvalue and eigenvector.

   

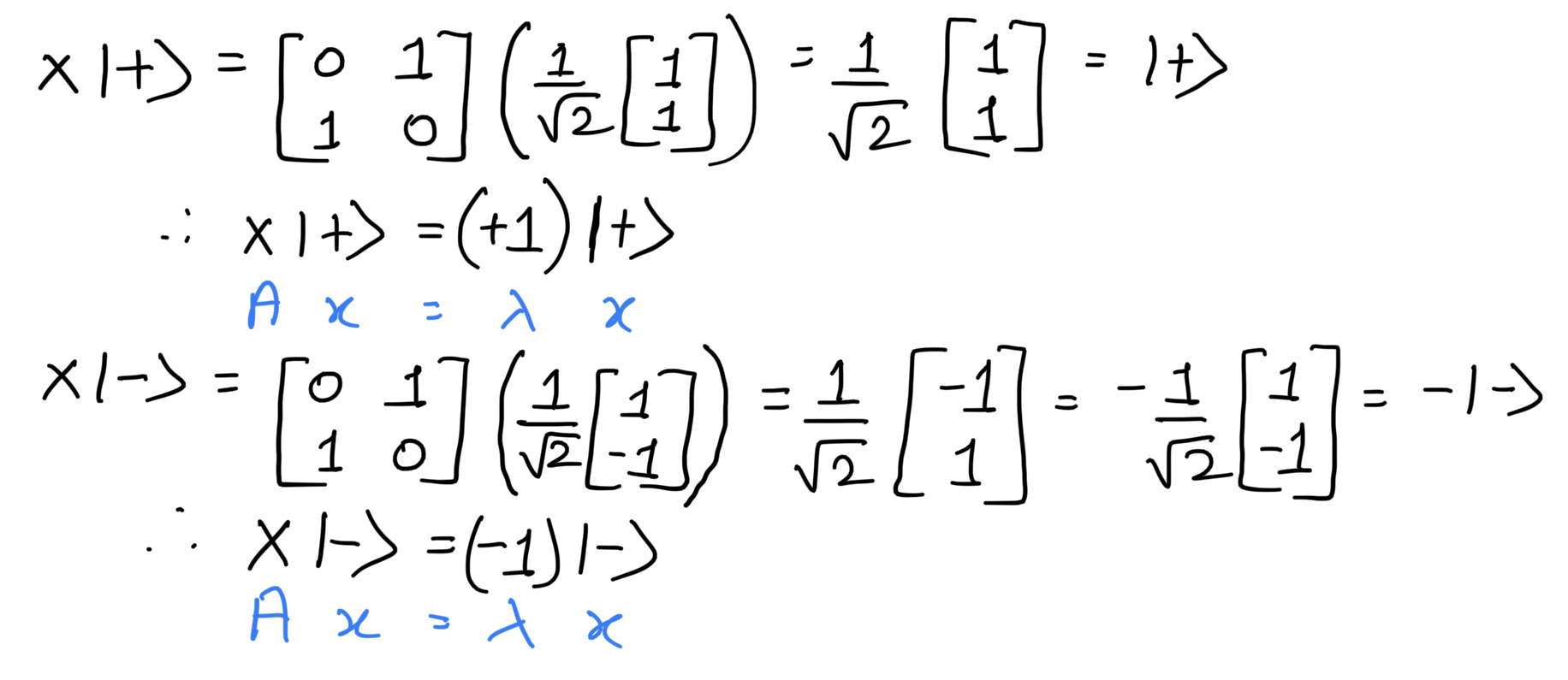
   Hence +1 and -1 are the eigenvalues and |+> and |-> are the eigenvectors of the Pauli-X matrix.

3. Pauli-Y Gate

   Consider the Y-Gate matrix

   

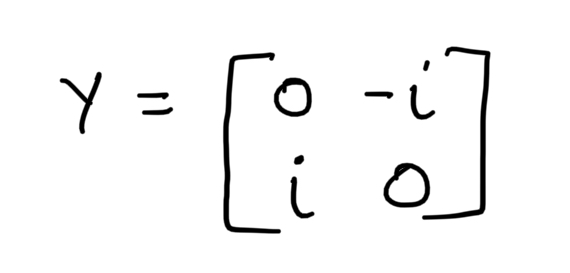
   Consider the states on the Y-axis.

   

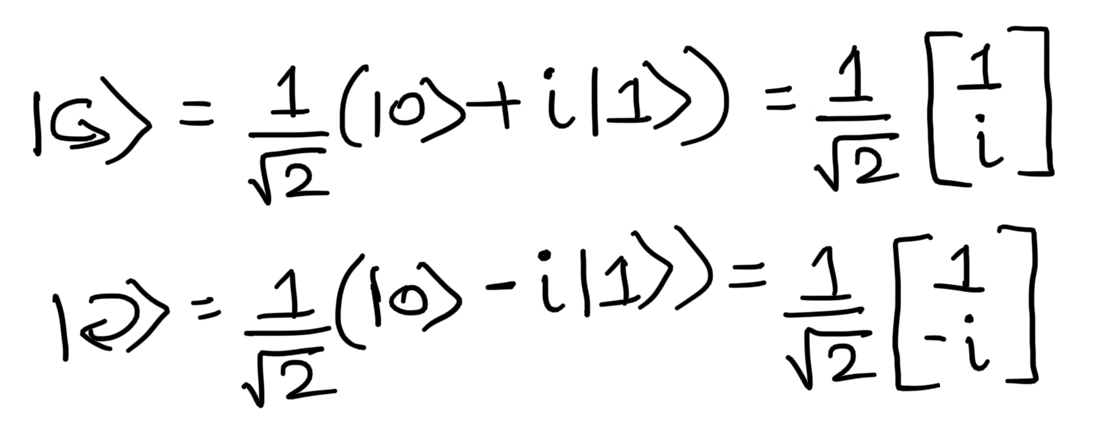
   Now let's check the equation for the eigenvalue and eigenvector.

   

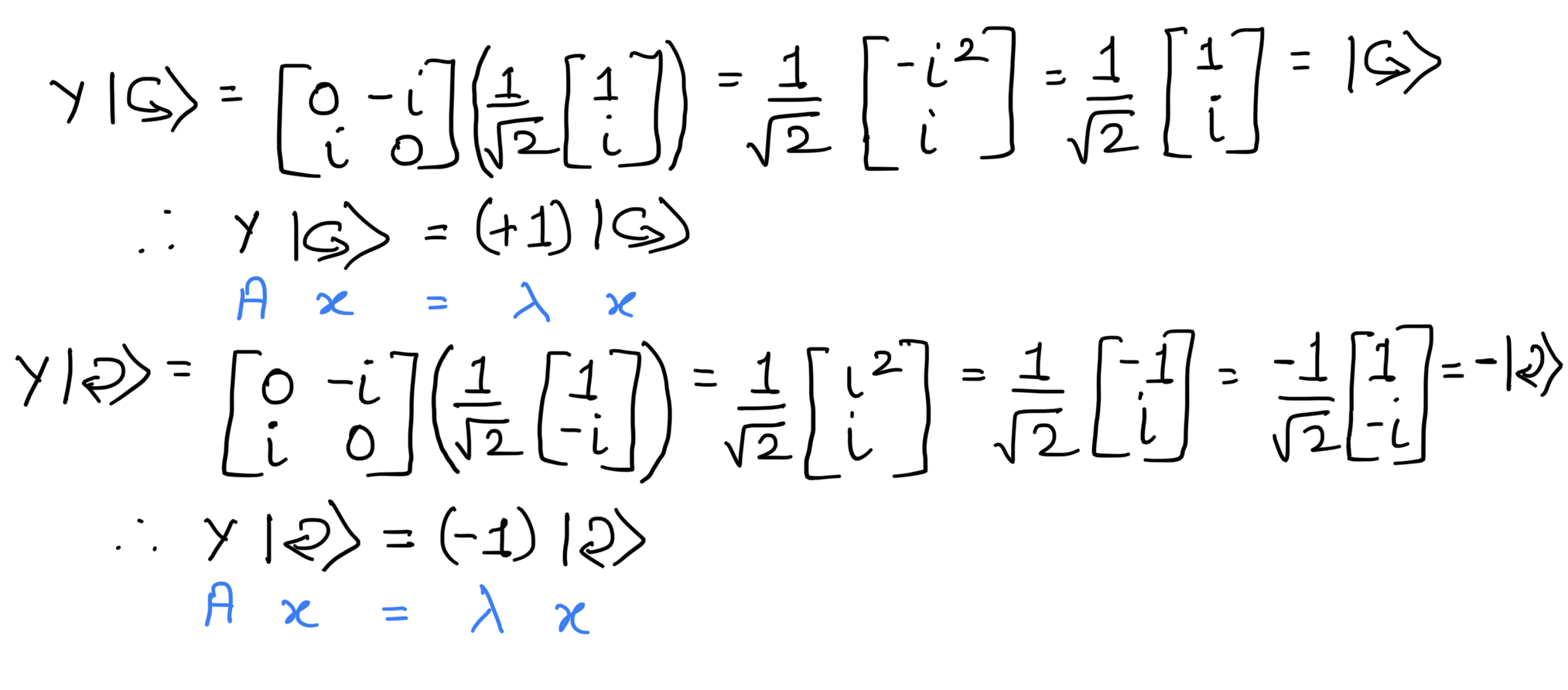
   Hence +1 and -1 are the eigenvalues and |↺> and |↻> are the eigenvectors of the Pauli-Y matrix.

Therefore, the states on the X, Y and Z axes of the Bloch sphere are the eigenstates of the Pauli-X, Pauli-Y, Pauli-Z matrix.

Inner Product:

It is a generalization of a dot product of two vectors. The result is scalar. The inner product of two orthogonal vectors is 0 and the Inner product of two same vectors is 1.

Z-axis states

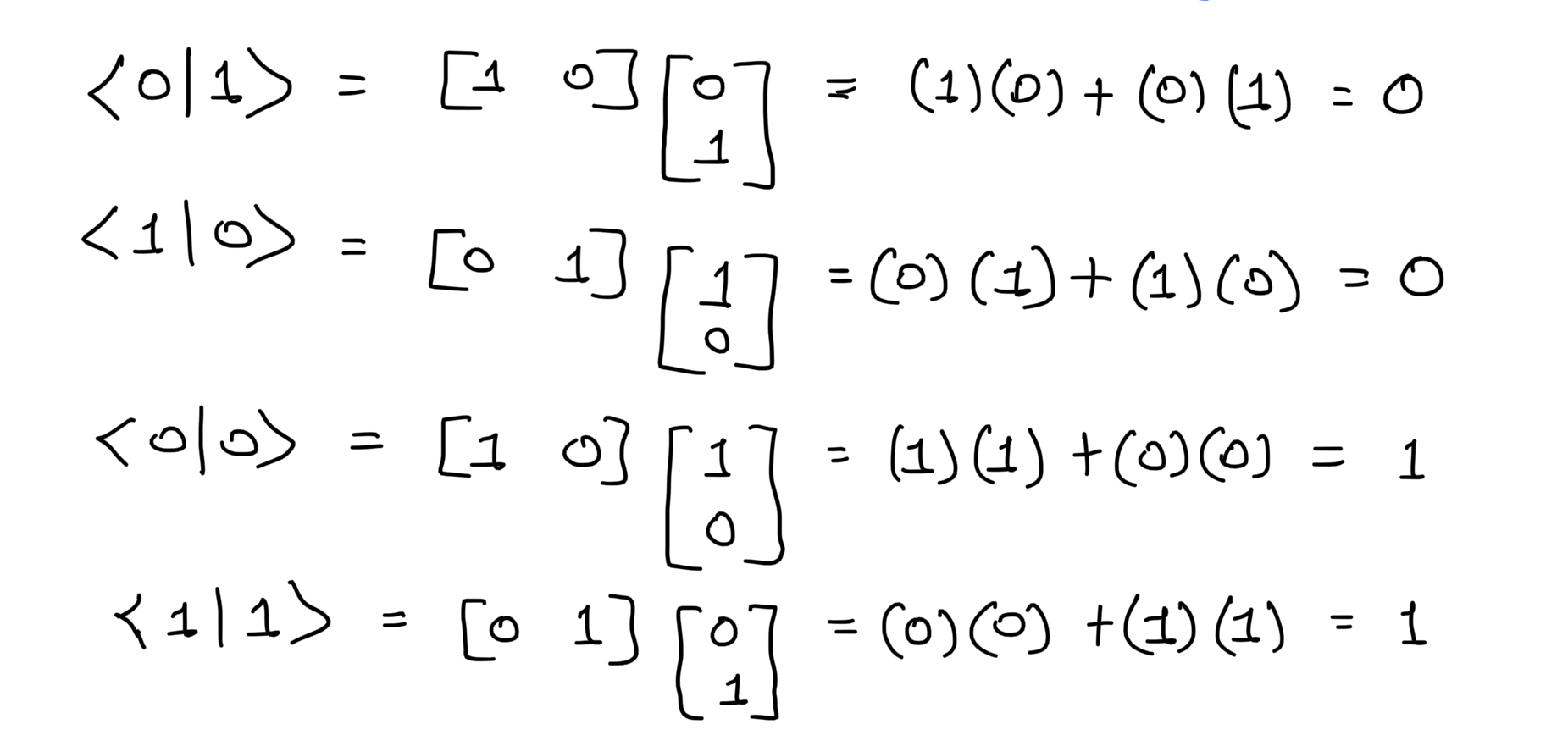
X-axis states

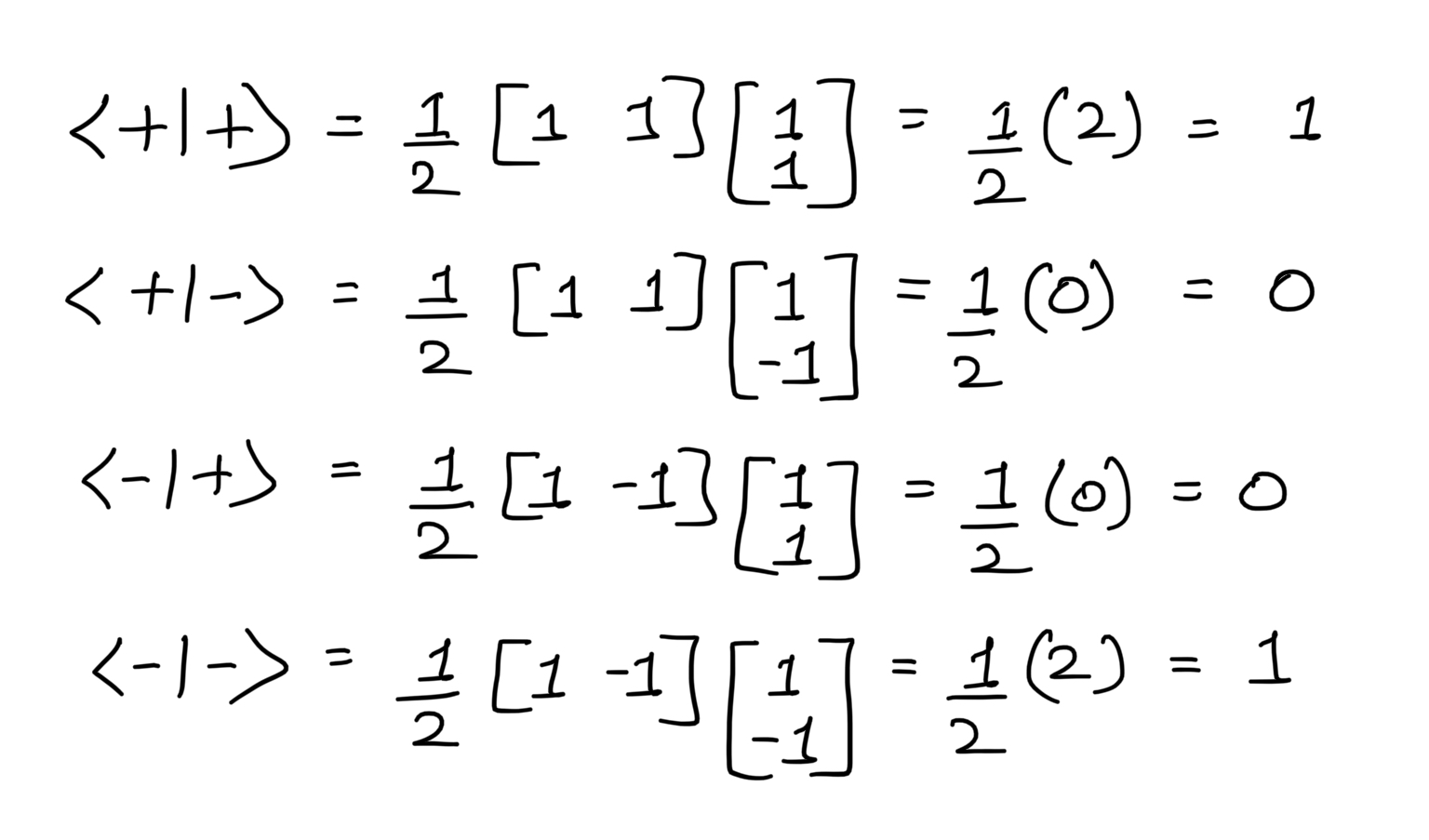
Y-axis states

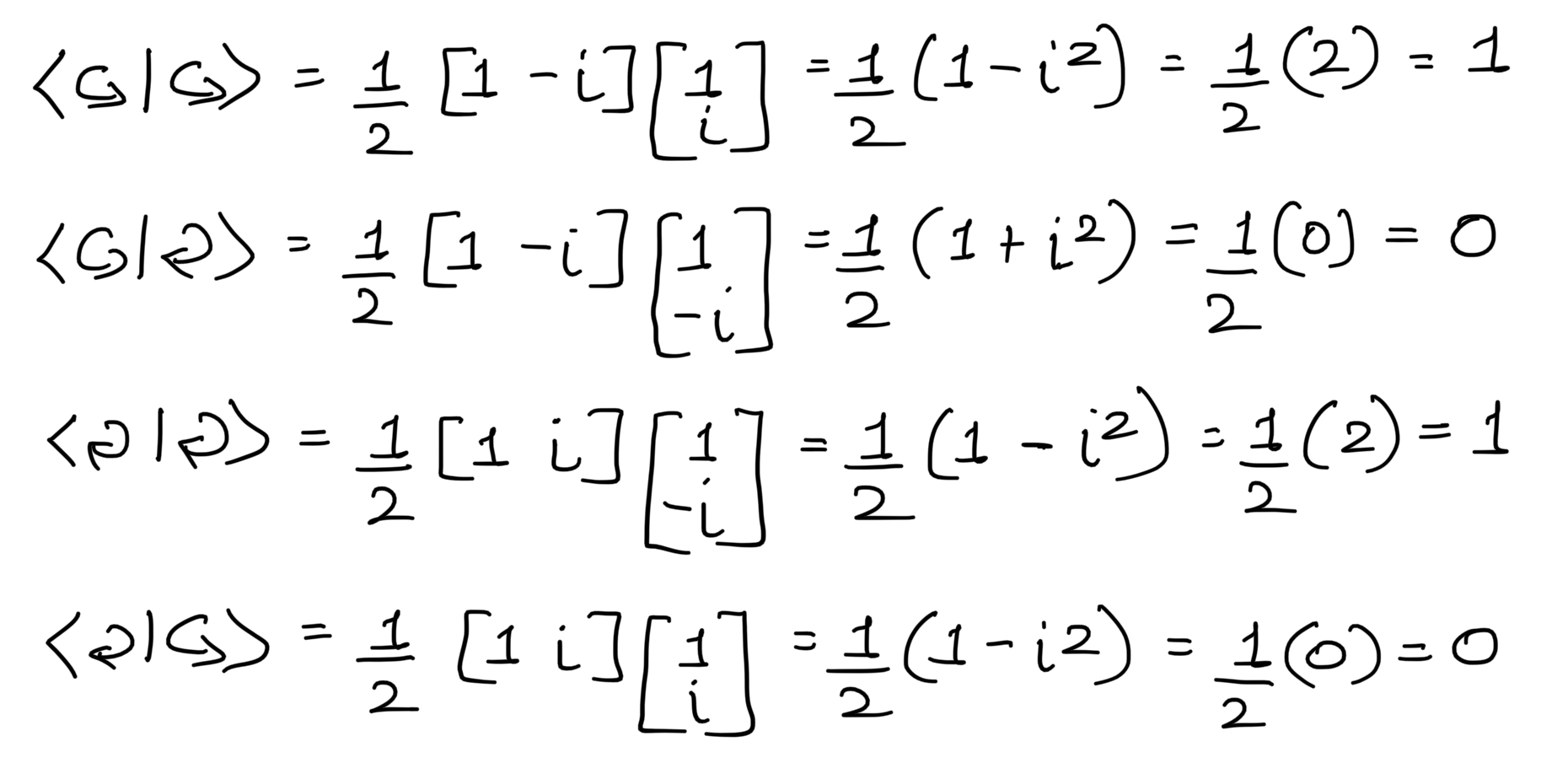
Coordinates of states on the Bloch Sphere:

To calculate the coordinates of the states we consider a different mathematical property known as the Expected Value of an Observable. An observable is an operator which acts on a quantum state to give its eigenvalue and the state changes to the eigenstate. If |Ψ> is a quantum state and 'M' is the observable then the average value or the expected value of the observable is given by <M> = <Ψ|M|Ψ>. It can also be used to calculate the coordinates of the Bloch Sphere.

States on the Z-axis

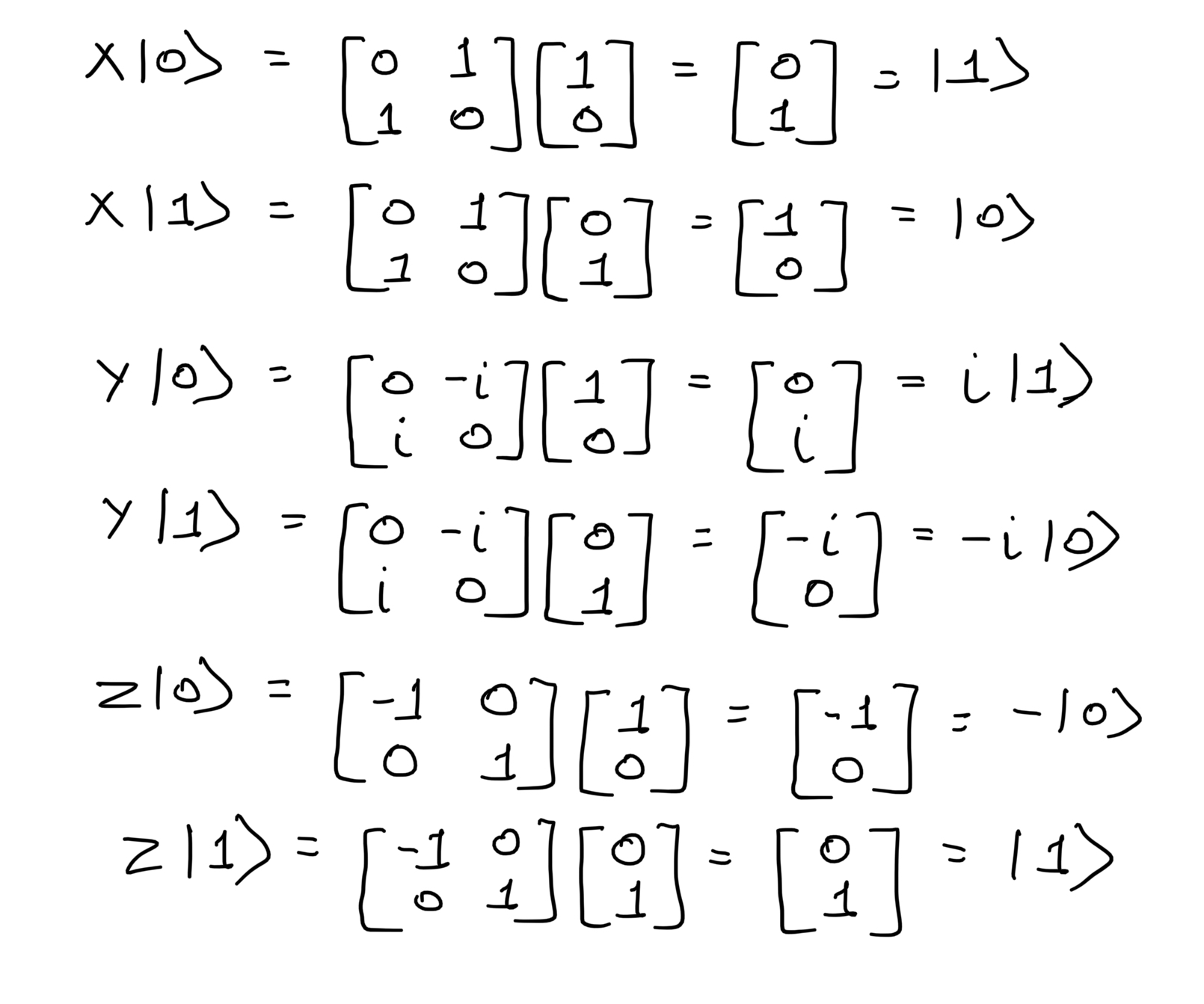
1. |0> state

   

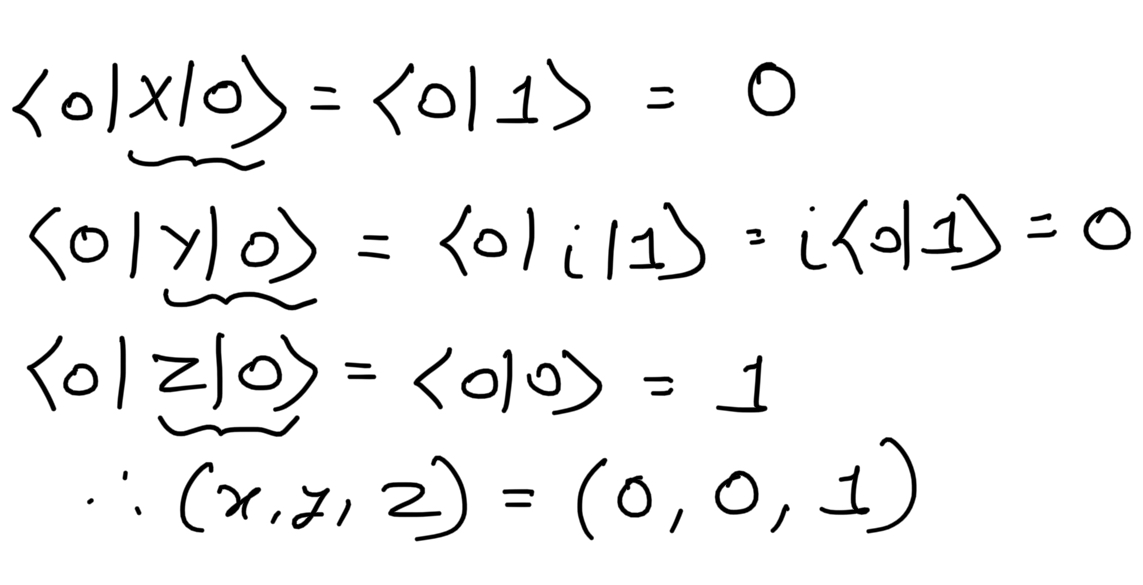
2. |1> state

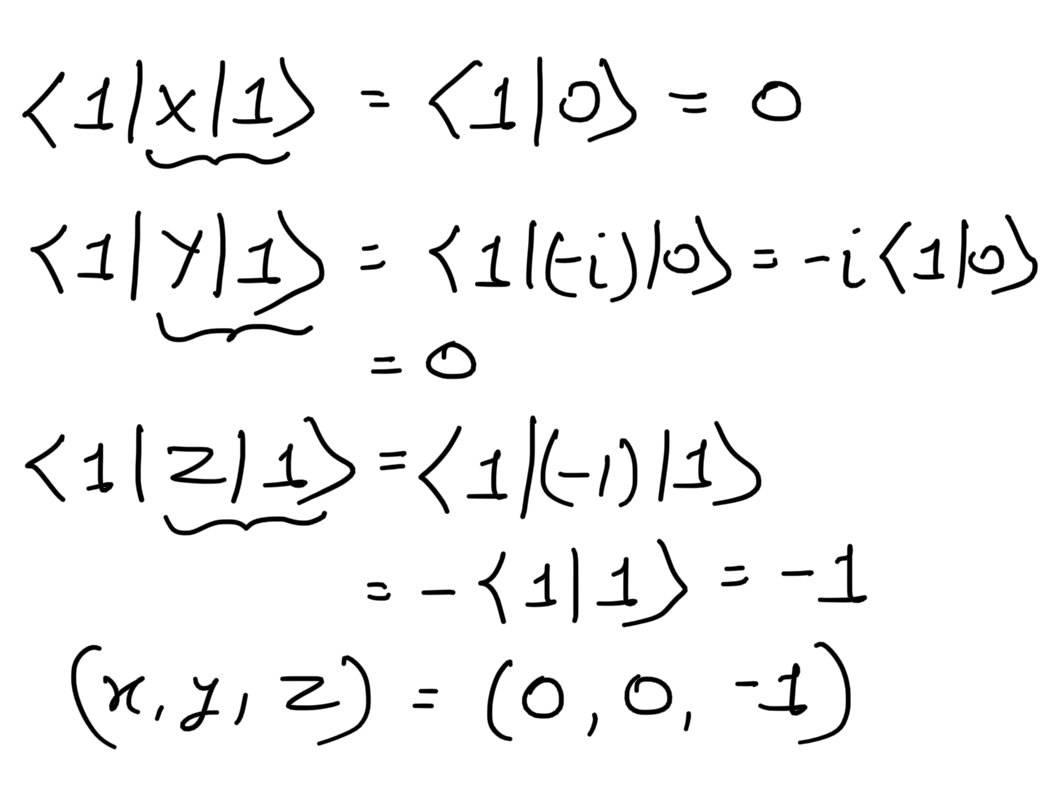
States on the X-axis

1. |+> state

   

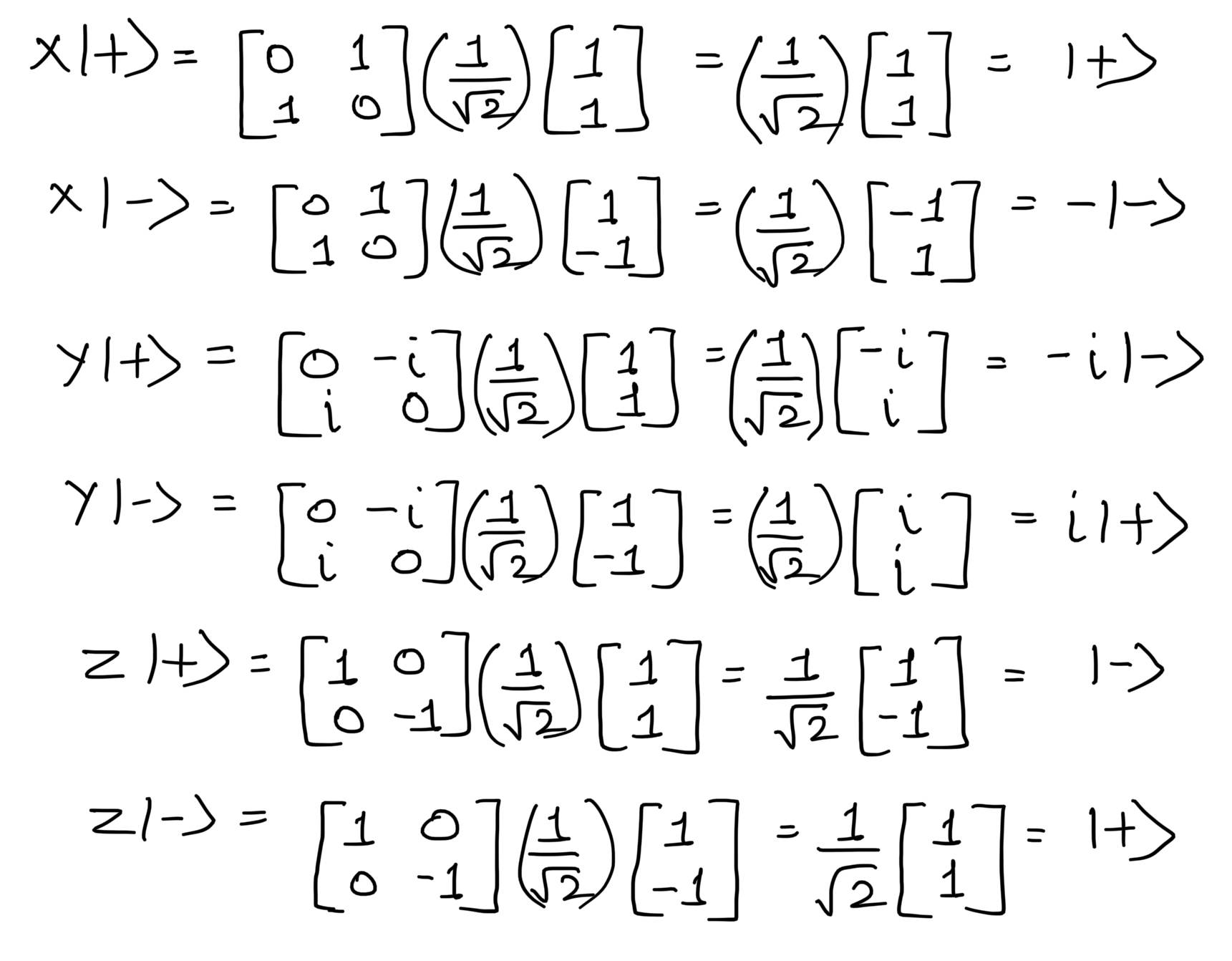
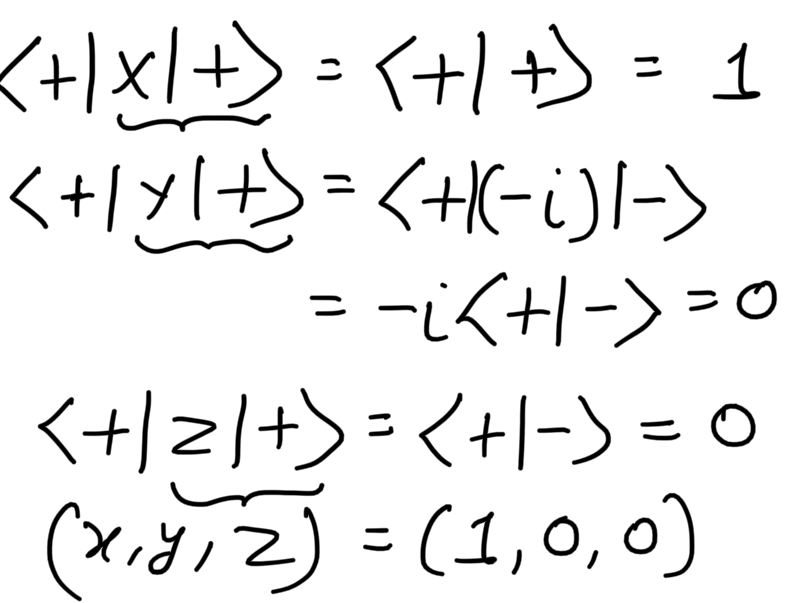
2. |-> state

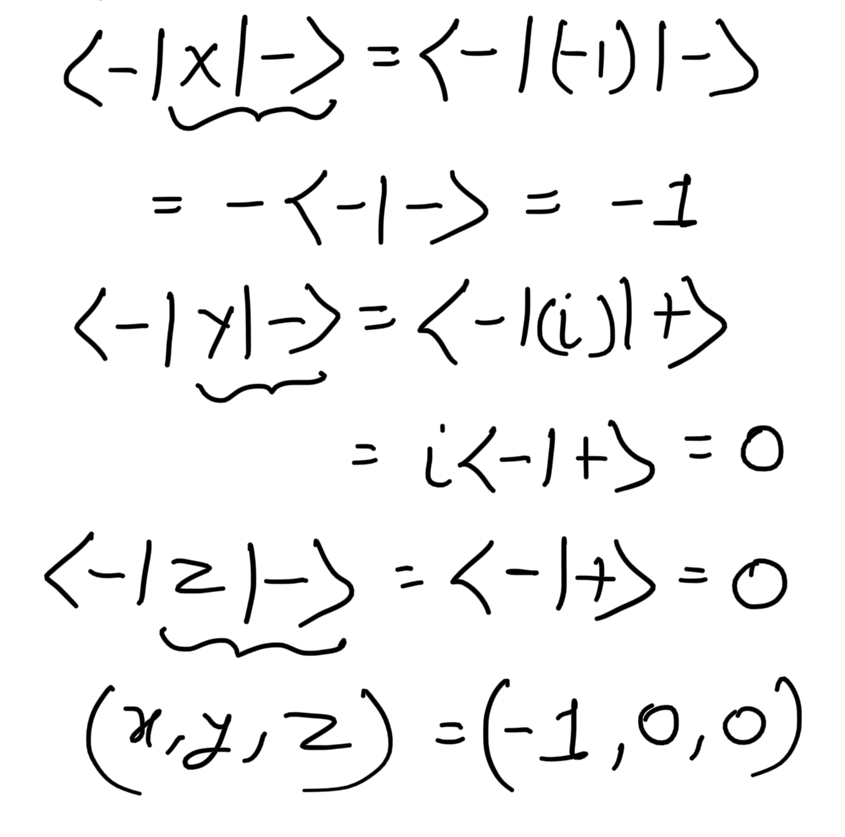
States on the Y-axis

1. |↺> state

   

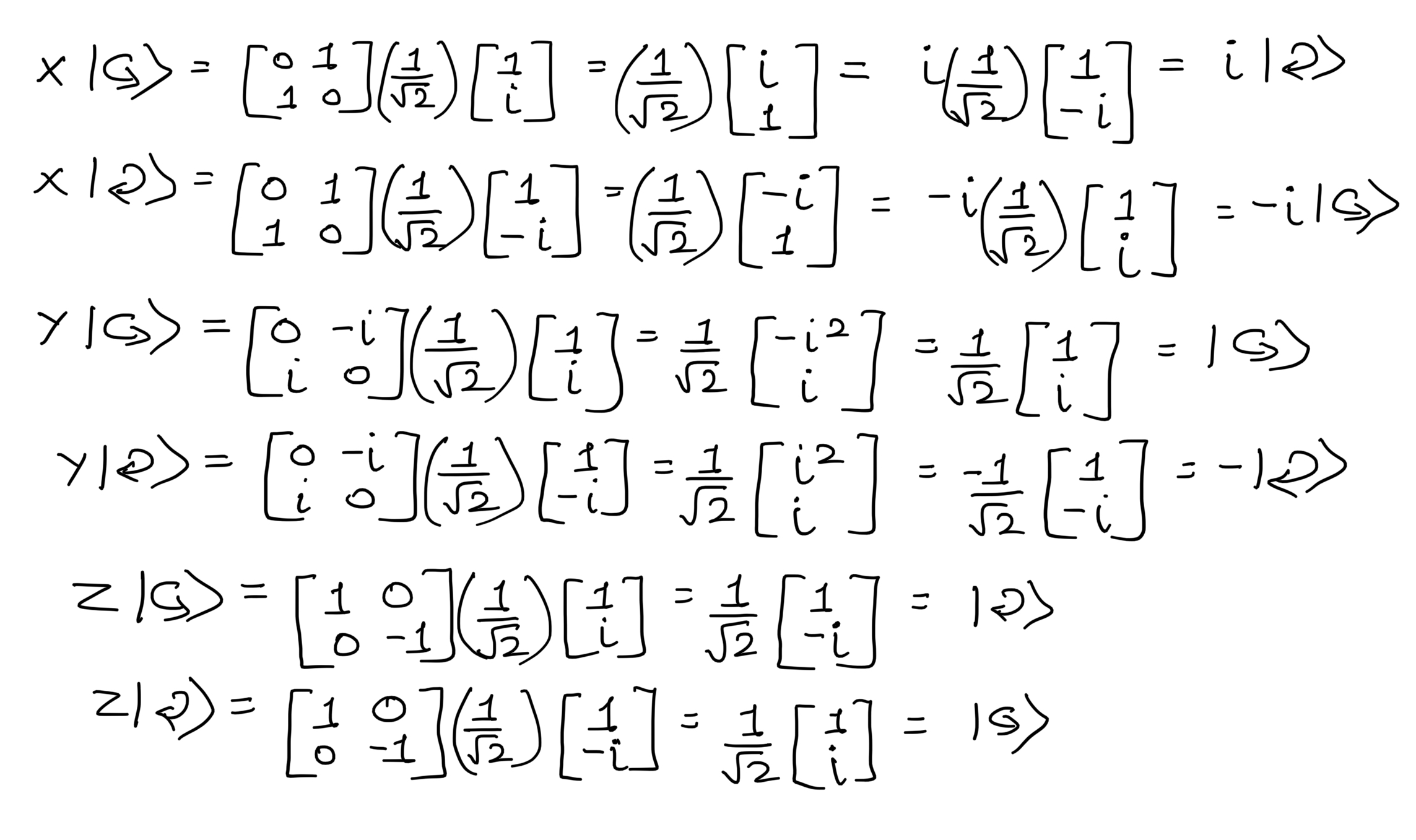
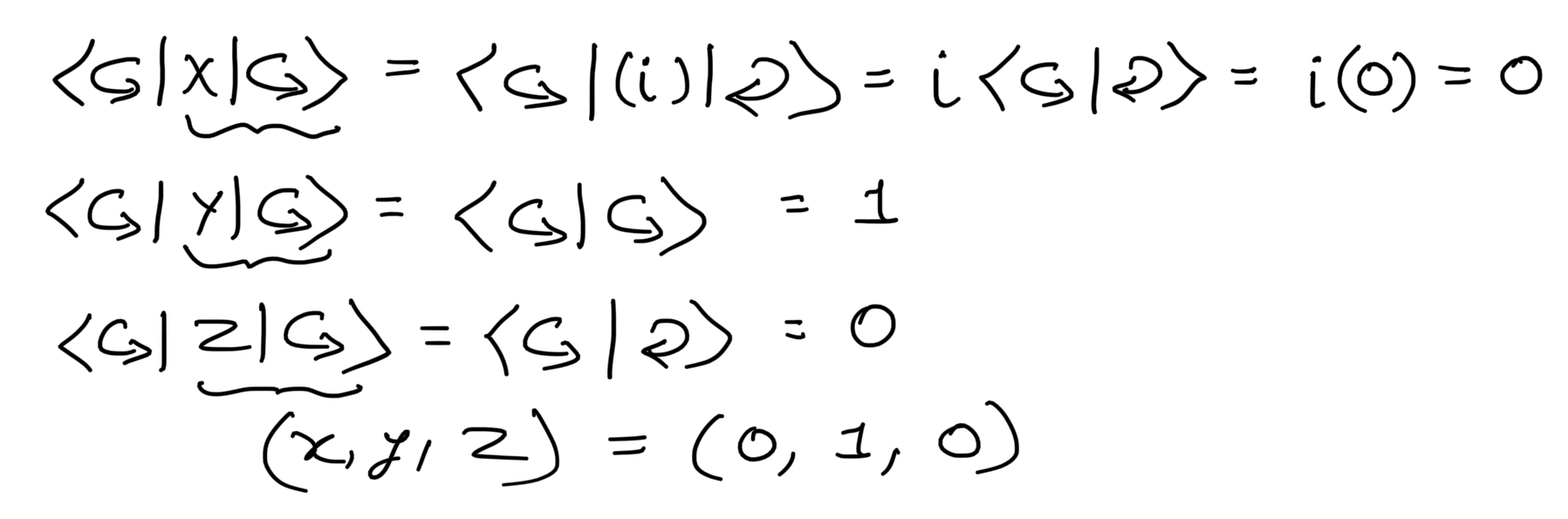
2. |↻> state

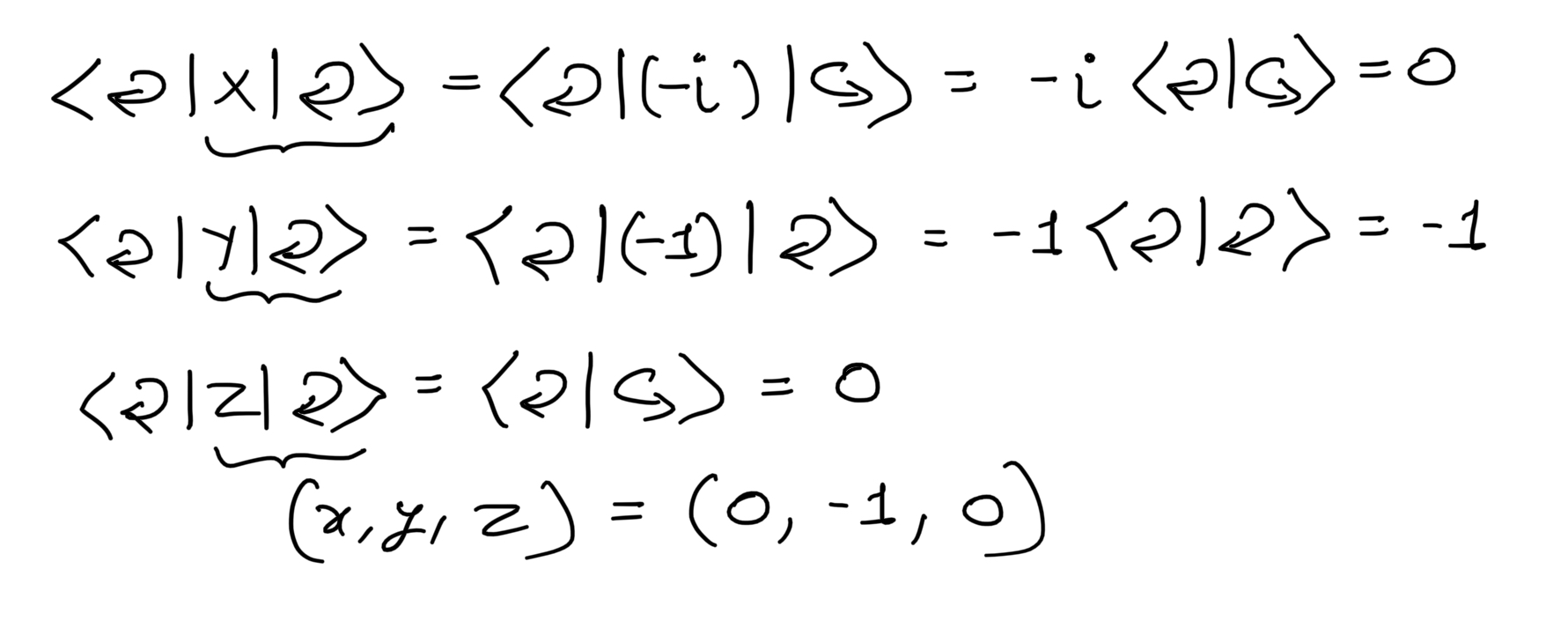
Rotations on Bloch Sphere and Trajectory

Let's consider the rotations around the Bloch Sphere. The rotation gates in quantum computing are Rx, Ry and Rz gates. X, Y and Z gates are special cases of Rx, Ry and Rz gates. These rotations around the Bloch Sphere are given by the Right-Hand Thumb Rule.

Right-Hand Thumb Rule: If the thumb of your right hand depicts the positive side of any axis(X, Y or Z) then the curled fingers depict rotation caused due to the gate.

1. X Gate: Rotation around X-axis (+X axis is right-hand thumb)

   

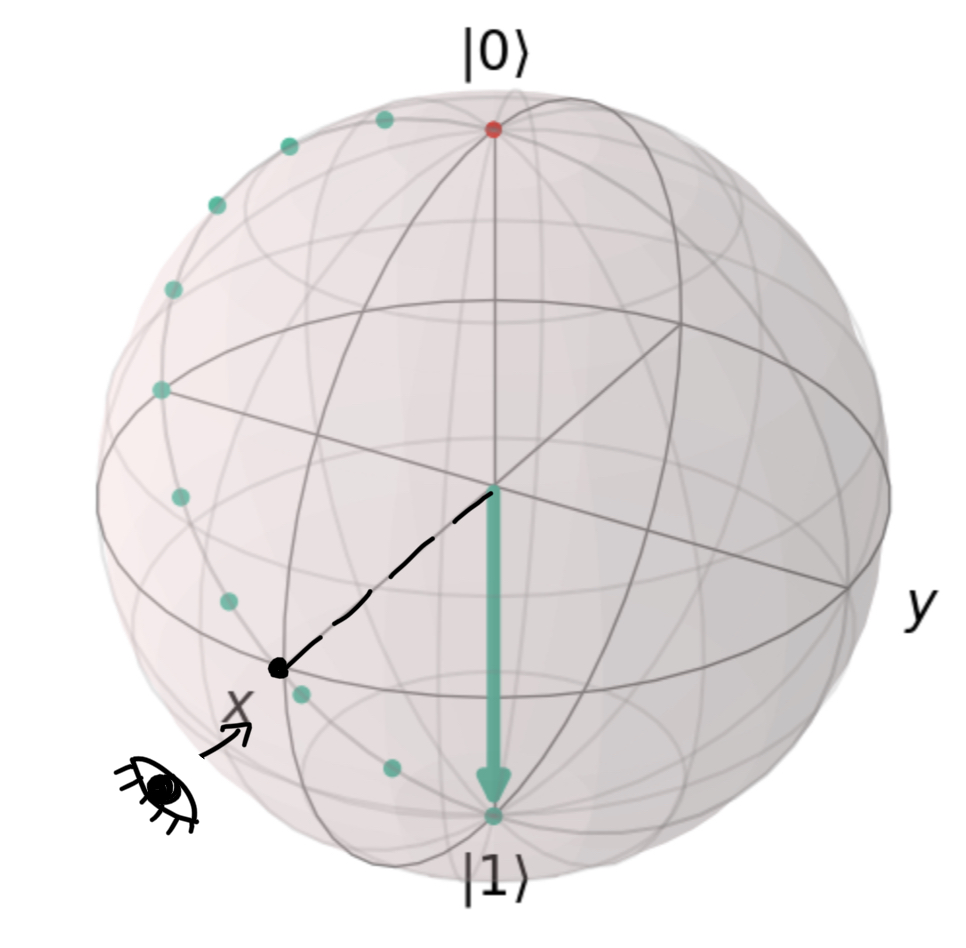
   Perpendicular view from the eye:

   

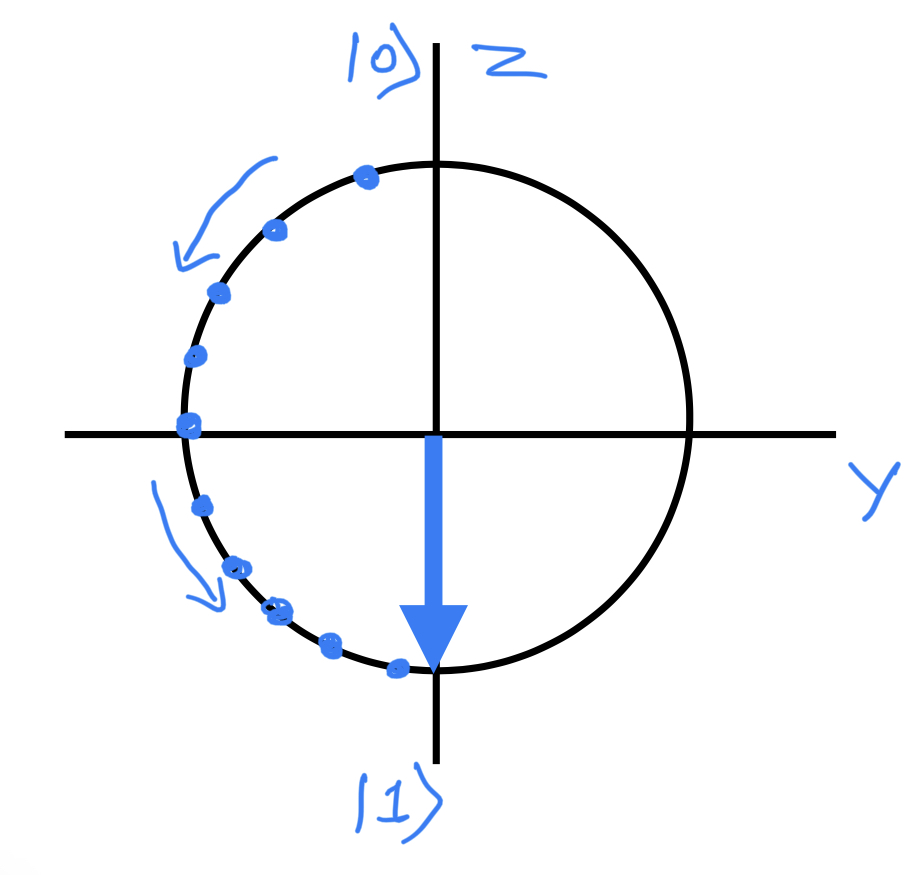
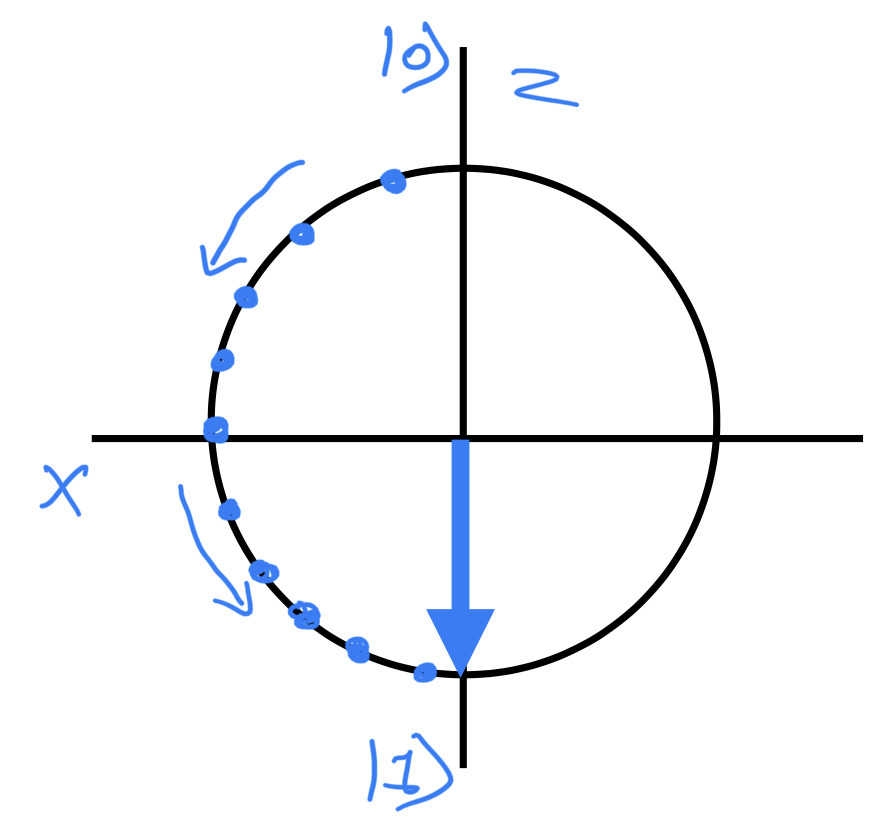
2. Y Gate: Rotation around the Y-axis (+Y axis is right-hand thumb)

   

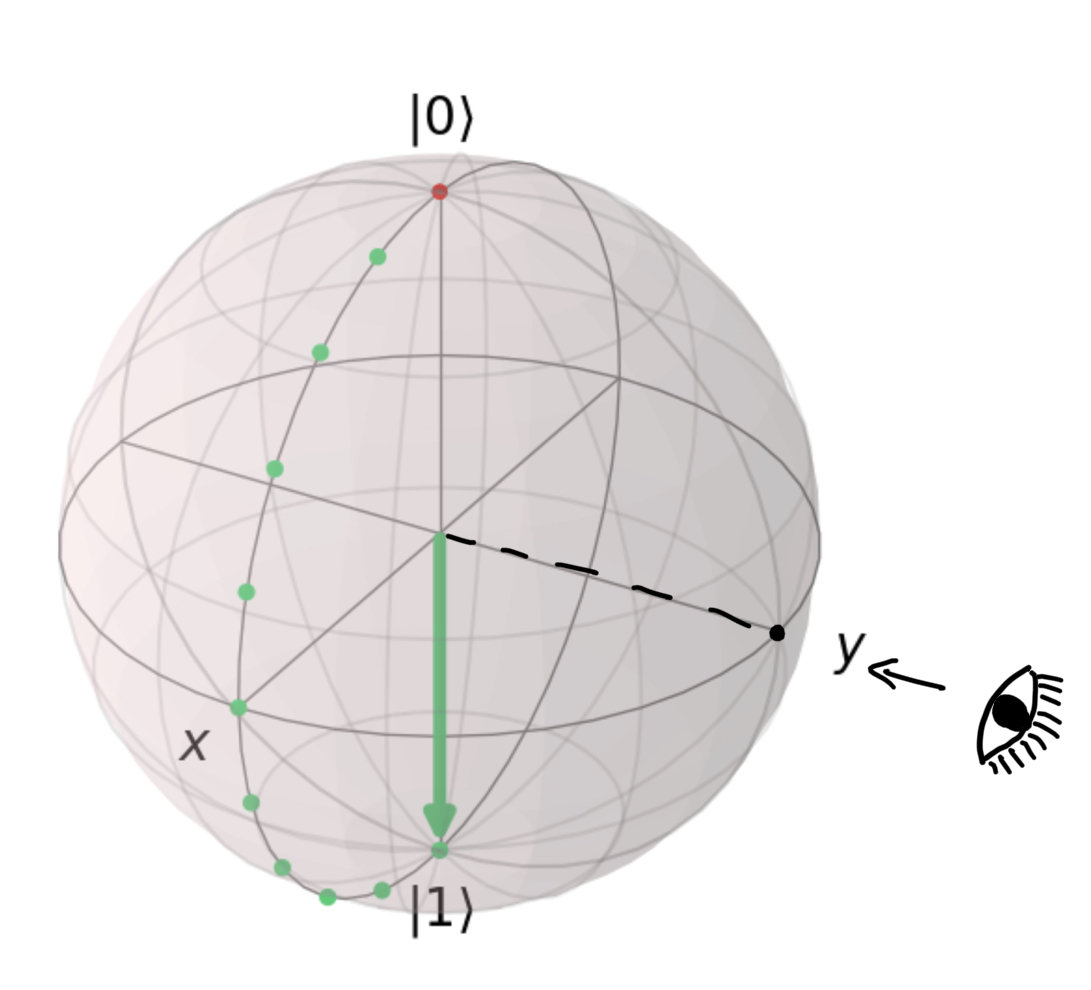
   Perpendicular view from the eye:

   

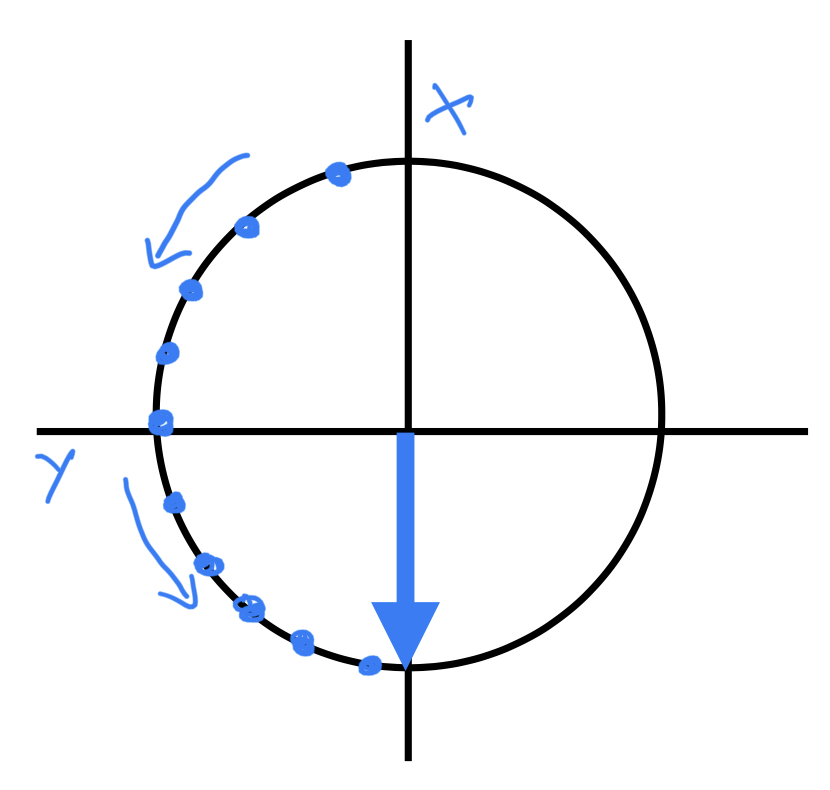
3. Z Gate: Rotation around the Z-axis (+Z axis is right-hand thumb)

   (Note: Ignore the grey dots here. To reach the |+> state on X-axis we have to apply H-Gate)

   

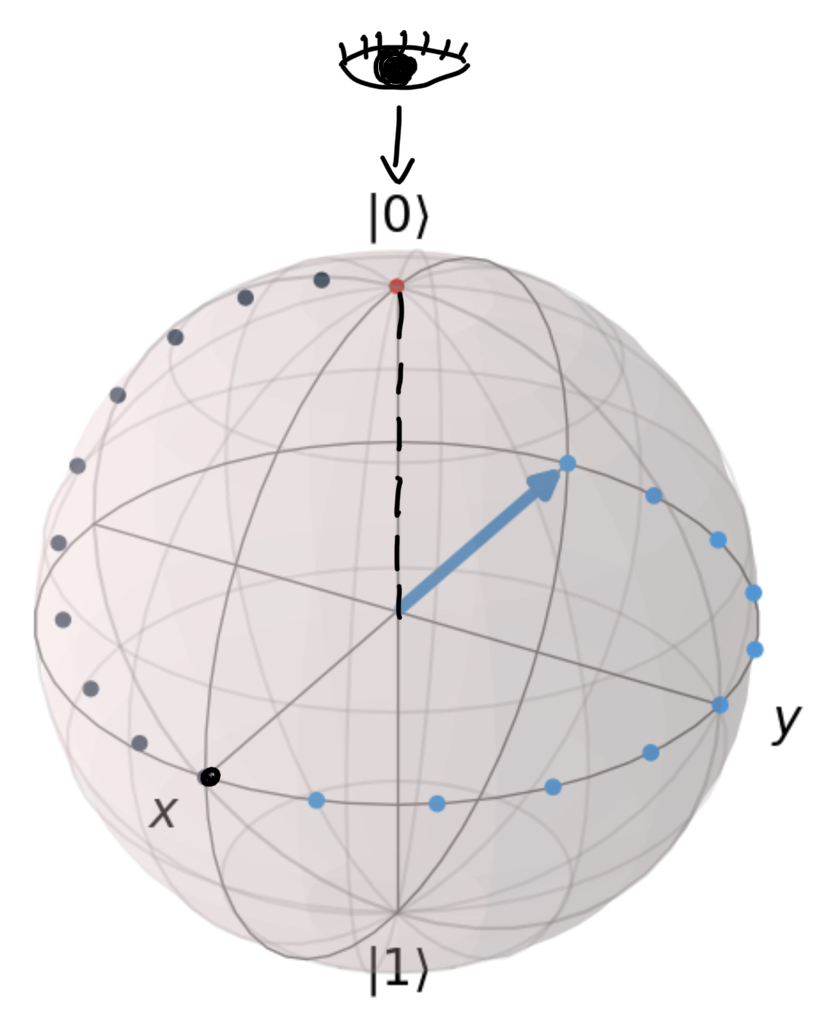
   Perpendicular view from the eye:

   

Code Snippet for one of the above traces:

From the above trace diagrams, we can conclude that rotation around the Bloch sphere happens in an anticlockwise direction when viewed from the positive side of an axis.

Conclusion

Hence Bloch Sphere is derived from the equation of the qubit. It is used to represent a single qubit state. There are different states associated with the X, Y and Z axes of the Bloch Sphere. Rotation around the Bloch Sphere is given by the right-hand thumb rule. However, these Bloch Sphere are not useful to represent entangled qubits. For that, we have a different visualization tool called the QSphere.

Thank you, IBM, QubitByQubit, and the Qiskit community.