INTRODUCTION

When I started to learn programming everything seemed to be simple and easy except for floating-point arithmetic. Yeah, you may argue with me that floating-point numbers are just numbers with decimal places like 1.1 and why would someone struggle with floating-point numbers? I would agree with you but I felt that there are more things to be unravelled with floating point numbers

For example, consider the following Python program

a = 0.1
while a != 5.0:
    a += 0.1
print(a)

When you perform the calculations on hand you would say that the program outputs 5.0 and terminates. But your calculations don't seem to explain what's happening here, The program does not produce any output.

Also here is another anomaly which I came across...

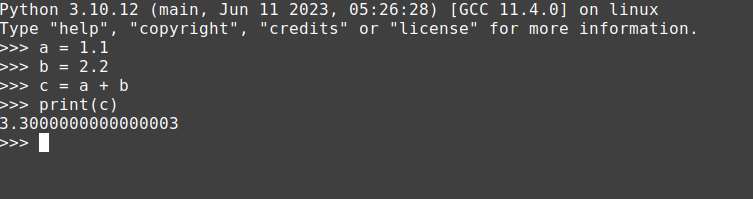
As we are always aware 1.1 + 2.2 is always 3.3 but, our python3 is telling us that 1.1 + 2.2 is 3.3000000000000003. You may argue that the error in this calculation is 0.0000000000000091% which is so small that it won't affect calculations. (Pardon me I am about to exaggerate things 😊😊) But we are ignoring the fact that computers are primarily designed for computational needs, even if it calculates such a small thing with error then how can we rely on computers for complex calculations?

WHAT'S GOING ON?

There is no machine with 100% efficiency.

On one thought you can understand that the loop never gets terminated(Of course, since there is no other part of the code that has the possibility of executing infinitely). But why would the loop never get terminated? Has not the terminal condition been reached? But when we do some manual calculations the loop must have terminated after 50 iterations, isn't it? Okay, fine let's see what's going on by changing the relational operator != into <.

a = 0.1
while a < 5.0:
    a += 0.1
print(a)

The program produces 5.099999999999998 as output and gets terminated. Now it is obvious that a never becomes 5.0 rather it becomes 5.099999999999998 which results in the infinite loop. But according to our calculations, the is no possibility for the variable a to be 5.099999999999998 since we are incrementing that variable by 0.1 in each iteration.

This happens due to an error in converting the human language into machine language. As you may be already aware, Machines cannot understand human language, numbers, or anything complex. They can understand only 1's and 0's as these are the only possible states of a transistor(ON and OFF). Everything that is stored in the computer is converted into 0 or 1 by the processor so, our numbers 0.1, 0.5 and 5.099999999999998 are converted into binary by the processor and then it is stored in the memory.

CONVERSIONS

we are familiar with the decimal number system(The number system with 10 symbols [0-9]). Now let's see a binary representation of a decimal number.

Consider the number 5.75 which is in the decimal number system. The binary equivalent of this decimal number is 101.11. The conversion of decimal to binary is explained below.

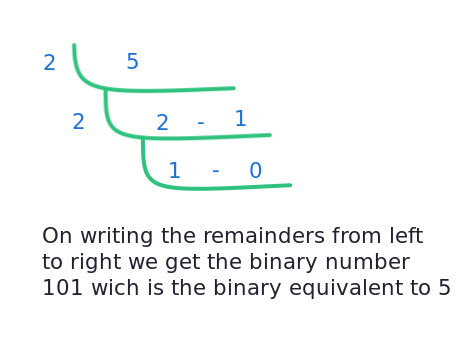
Now everything seems to be simple

• For every number that is in the decimal number system, there exists a unique binary equivalent.

• The binary equivalent is unambiguous.

But the above points are completely wrong

• For every Binary number, there exists a unique decimal number but the converse cannot be true in all cases.

• The binary-to-decimal conversion is unambiguous but the decimal-to-binary conversion may not be always unambiguous.

Am I concluding that the systems that humans developed over long generations are error-prone and cannot do some basic calculations? Technically yes, But am I saying it without any form of proof? No!

ERRORS IN CONVERSIONS

Consider a simple number say 1.1 Now let's try to convert it into binary

Firstly for the decimal part 1, the binary value is simply 1

Secondly for the fractional part 0.1 the binary conversion takes place as follows

So when should I terminate this process? Are there any standard rules about when to stop performing this infinite multiplication operation? Sadly the answer would be no and then a yes...

REASON FOR NO PROPER STANDARDS:

But, Why aren't there any standard rules or procedures(There is actually IEEE - 754 we will discuss this in a later part) on when to stop iterating through even though these operations are carried out repeatedly over and over on a certain set of numbers?

The Path towards accuracy became a path towards inaccuracy

The answer is very simple, If you terminate the repeated multiplication operation after you find out there is a circular multiplication operation the resultant binary number would be less accurate i.e., It may not represent the actual decimal number in binary format

Consider the example below...

Now a common question arises in your mind. "Then how the floating point numbers are internally represented in the memory if there is no standard set of rules?".

Now comes the latter part "YES":

Even though any standard could be inaccurate there has to be something that ensures interoperability or else each system produces a different binary number for the same decimal number which introduces ambiguity among systems. So there has to be a standard even though it has its own limitations.

One such standard is IEEE - 754

IEEE - 754

You can find a detailed overview of this standard on IEEE -754 GEEKS FOR GEEKS

Now focusing only on the essential details of double precision:

The IEEE-754 suggest us to divide the binary number into three parts

• The signed bit

• The Exponent part

• The Normalized Mantissa part

Signed Bit(1 bit) - Represent whether the given binary number is positive or negative.

Exponent Part(11 bits) - Represents the exponent of the number in binary.

Normalized Mantissa Part(52 bits) - Represents the fractional part of the number in binary.

Converting decimal numbers into IEEE 754 double-precision numbers

Let's discuss our anomaly 1.1 + 2.2 != 3.3.

Things that we are about to discuss:

1. Converting 1.1 and 2.2 into their IEEE - 754 representations.

2. Summing up 1.1 and 2.2 and get the result (I mean summing up their scientific notations).

3. Checking our result with the value that is stored by python3.

Let's convert the number 1.1 to its IEEE - 754 representation

Step 1:

The number 1.1 in binary can be expressed as

1. 00011001100110011...

Step 2 (Scientific Notation):

1.00011001100110011... x 2 ^ 0

calculating biased exponent -> 1023 + 0 = 1023

converting 1023 to binary -> 01111111111 (11 bits)

Step 3 (IEEE Notation):

1. Signed Bit -> 0(Since the given number is positive)

2. Exponent Part -> 01111111111

3. Normalized Mantessa Part -> 0001100110011001100110001100110011001100110011001100

Combining the three parts and the resultant binary number will be

0 01111111111 0001100110011001100110011001100110011001100110011010

Let me just divide the binary numbers into nibbles which could make things easier to visualize

0011 1111 1111 0001 1001 1001 1001 ...

so the Hexa decimal value would be 3 f f 1 9 9...

Now for 2.2, the IEEE 754 value would be

0 100000000000 00011001100110011....

Scientific Notation: 1.0001100110011001100110011... x 2 ^ 1

Now we know the scientific notations of both 1.1 and 2.2 we can add them...

the result would be

1. 1010 0110 0110 0110 ... 0101 x 2 ^ 1

The calculations are as follows...

On reconverting this binary number into decimal the desired 3.3 but converting this binary number to decimal would result in 3.299999999

From this, we can conclude that there is an inaccuracy in floating point arithmetic operations....

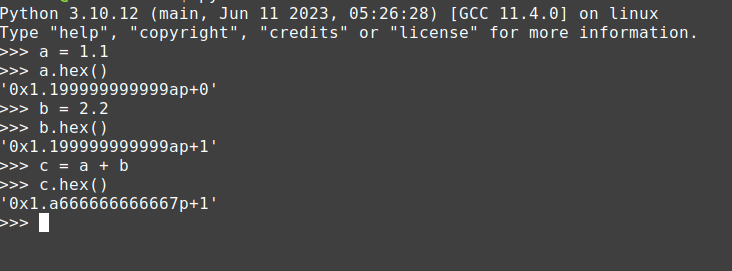
Let's compare our results with the values that are processed by python3

Conclusion

Now pretty much everything is clear...

From this, we can conclude that

1. Representing floating point numbers in binary is a difficult task.

2. Even though using standards like IEEE - 754 we may face inaccuracy.

3. We should be careful while working with floating point numbers.

Now here comes the next question

our result for 1.1 + 2.2 is 3.299999999 but python3 produces an output of 3.3000000000000003 why is there a difference? (But both the hexa decimal representations are same)

The answer to this is more Pythonic than floating point inaccuracies, So let's talk about this in an upcoming blog.