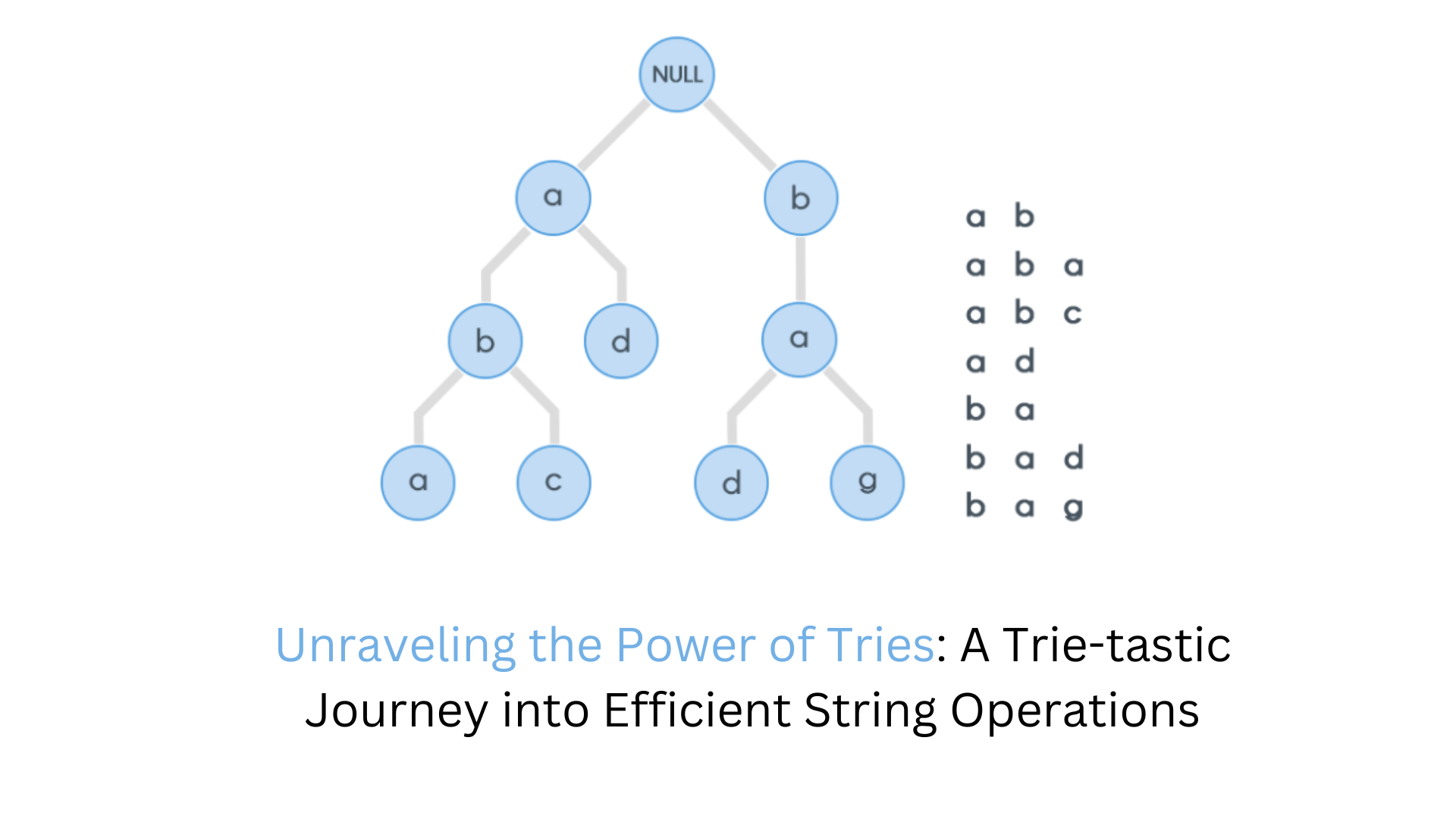
Introduction to Tries

A Trie short for retrieval tree or digital tree, is a tree-like data structure used primarily for efficient and fast string-related operations, especially when dealing with dynamic sets of strings or keys. A Trie is characterized by the following key features:

Tree Structure: Tries use a tree-like structure with nodes representing characters.
Nodes and Edges: Each node represents a character, connected by labeled edges. Paths from the root form strings, e.g., 'c', 'a', 't' for "cat."
Efficient Retrieval: Quick searches (O(L)) for words where L is the length of the word, perfect for extensive datasets.
Space Usage: space complexity for storing words O(N), where N is the total number of characters in all the words stored in the Trie. Each character in each word is stored as a node in the Trie

this is how a Trie look like

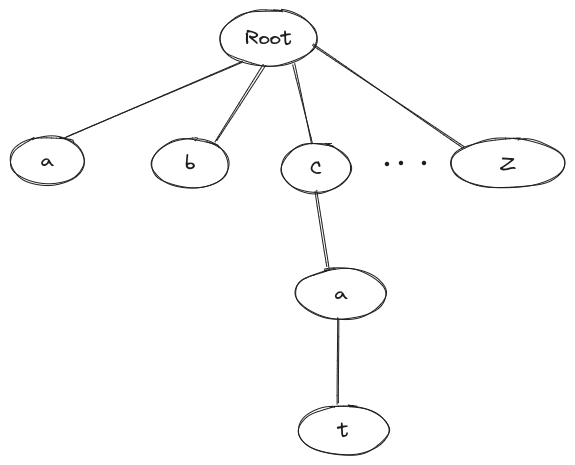
Why use Trie

Tries and Hash Maps can have similar time complexities of O(L) for insertion, deletion, and search operations (where L is the length of the word). However, Trie data structures often consume less space compared to Hash Maps, and here's why:

Word Storage: In Tries, the space usage primarily depends on the number of unique characters in your dataset, not the total number of words. For Hash Maps, you need to store the entire word as a key along with any associated values, which can be less space-efficient, especially when dealing with a large number of words.
Space Optimization: Various space optimization techniques can be applied to Tries. For instance, Patricia Tries (Radix Tries) compress common prefixes further, saving even more space.
Sparse Data Handling: Tries are particularly efficient when dealing with sparse data, where there are many words with shared prefixes. In such cases, Hash Maps may have a higher memory overhead due to storing complete words separately.

In a Hash Map, when creating four different words, each word is stored as a separate key-value pair. Even if two words share a common prefix, such as 'rat' and 'rap,' the Hash Map would store both words in their entirety

In a Trie, when creating four different words, the Trie efficiently reuses characters for common prefixes. For example, if you insert 'rap' and 'rat' into a Trie, the characters 'r,' 'a', in the common prefix 'ra' are shared between both words. This sharing of characters and prefixes makes Tries more space-efficient in scenarios where words have common beginnings

Basic operations of Trie

code :

#include <iostream>
#include <vector>
using namespace std;

// Define a class for Trie node
class tnode {
public:
  char val;                  // The character stored in this node
  vector<tnode *> children;  // An array to store child nodes for each alphabet (26 in total)
  bool isTerminal;           // Flag to mark if this node represents the end of a word

  // Constructor to initialize a Trie node with a character 'ch'
  tnode(char ch) {
    val = ch;
    children.assign(26, NULL);  // Initialize the children vector with 26 NULL pointers
    isTerminal = false;         // Initialize isTerminal as false
  }
};

// Define a Trie class
class Trie {
public:
  tnode *root;  // Pointer to the root of the Trie

  // Constructor to initialize a Trie with an empty root
  Trie() {
    root = new tnode('\0');  // The root node has a special character '\0'
  }
  // Function to insert a word into the Trie
  void insertnode(tnode *root, string word) {
    tnode *cur = root;
    // Traverse the Trie based on each character of the word
    for (int i = 0; i < word.size(); i++) {
      int ind = word[i] - 'a';  // Calculate the index for the character
      if (cur->children[ind] == NULL) {
        // If the child node for the character doesn't exist, create a new node
        tnode *newnode = new tnode(word[i]);
        cur->children[ind] = newnode;  // Link the new node to the current node's children
      }
      cur = cur->children[ind];  // Move to the next node in the Trie
    }
    cur->isTerminal = true;  // Mark the last node as the end of a word
    return;
  }
  // Function to insert a word into the Trie (using the root of the Trie)
  void insert(string word) {
    insertnode(root, word);
  }

  // Function to search for a word in the Trie
  bool searchtnode(tnode *root, string word) {
    tnode *cur = root;
    // Traverse the Trie based on each character of the word
    for (int i = 0; i < word.size(); i++) {
      int ind = word[i] - 'a';  // Calculate the index for the character
      if (cur->children[ind] == NULL) {
        // If the child node for the character doesn't exist, the word is not in the Trie
        return false;
      }
      cur = cur->children[ind];  // Move to the next node in the Trie
    }
    return cur->isTerminal;  // Check if the last node represents the end of a word
  }

  // Function to search for a word in the Trie (using the root of the Trie)
  bool search(string word) {
    return searchtnode(root, word);
  }
  // Function to search for a prefix in the Trie
  bool searchpre(tnode *root, string word) {
    tnode *cur = root;
    // Traverse the Trie based on each character of the word
    for (int i = 0; i < word.size(); i++) {
      int ind = word[i] - 'A';  // Calculate the index for the character
      if (cur->children[ind] == NULL) {
        // If the child node for the character doesn't exist, the prefix is not in the Trie
        return false;
      }
      cur = cur->children[ind];  // Move to the next node in the Trie
    }
    return true;  // If the prefix exists in the Trie, return true
  }
  // Function to check if a word with a given prefix exists in the Trie
  bool startsWith(string prefix) {
    return searchpre(root, prefix);
  }
};
int main() {
  Trie *a = new Trie;
  // Insert the word "MET" into the Trie
  a->insert("MET");
  a->insert("MEAT");
  // Search for the word "MET" in the Trie and print the result (should be true)
  cout << a->search("MET");
  return 0;
}

Insertion of word:

The code starts by defining a Trie node class (tnode) and a Trie class (Trie), which are used to represent the Trie data structure.
In the main() function, an instance of the Trie class a is created.
The word "MET" is inserted into the Trie using the insert function:
- The insert function internally calls the insertnode function with the root of the Trie and the word "MET."
- The insertnode function initializes cur as a pointer to the root of the Trie and begins traversing the Trie based on each character of the word.
- First, it processes 'M':
  - It calculates the index for 'M' as 12 ('M' - 'A' = 12).
  - Since the children vector of the root is initially filled with NULL pointers, it creates a new node for 'M' and sets it as a child of the root.
- Next, it processes 'E':
  - It moves to the 'M' node (the child of the root).
  - It calculates the index for 'E' as 4 ('E' - 'A' = 4).
  - Since the 'M' node doesn't have a child for 'E' yet, it creates a new node for 'E' and sets it as a child of the 'M' node.

Finally, it processes 'T':

It moves to the 'E' node (the child of the 'M' node).
It calculates the index for 'T' as 19 ('T' - 'A' = 19).
Since the 'E' node doesn't have a child for 'T' yet, it creates a new node for 'T' and sets it as a child of the 'E' node.
- After processing all characters in "MET," it marks the 'T' node as a terminal node by setting isTerminal to true. This indicates that "MET" is a complete word in the Trie.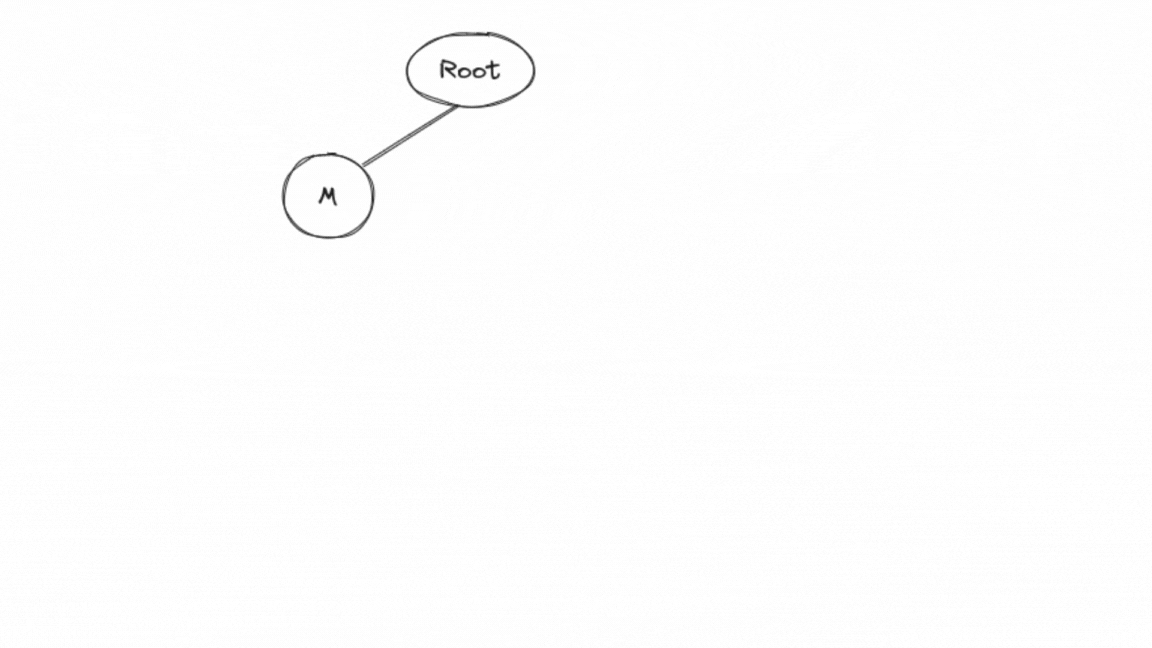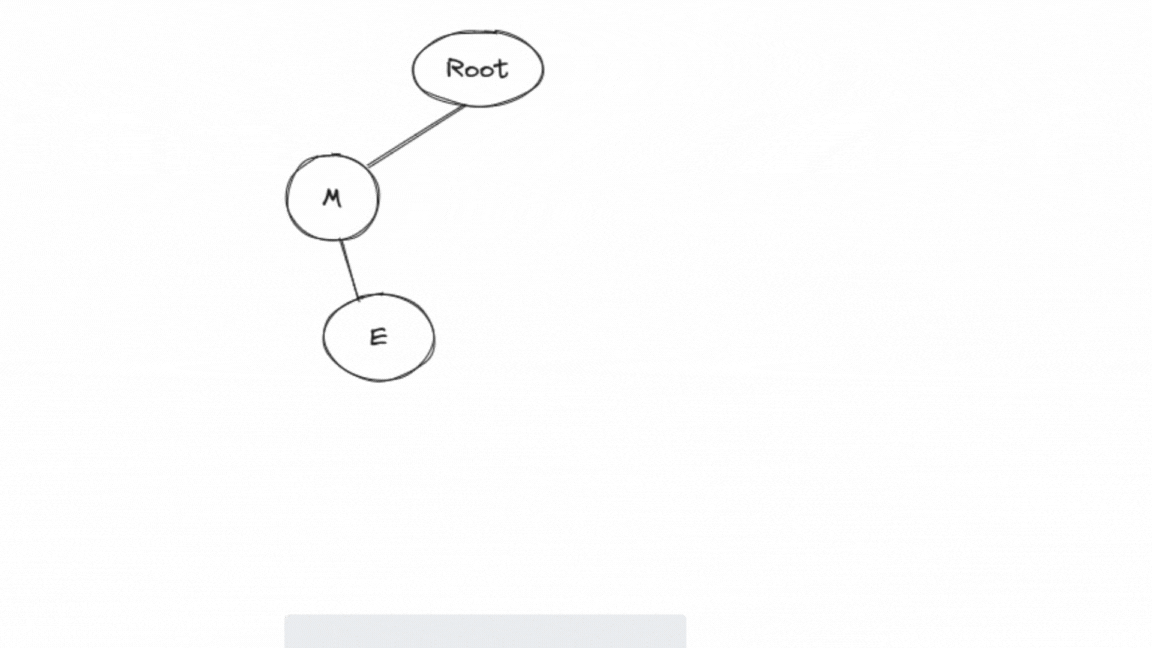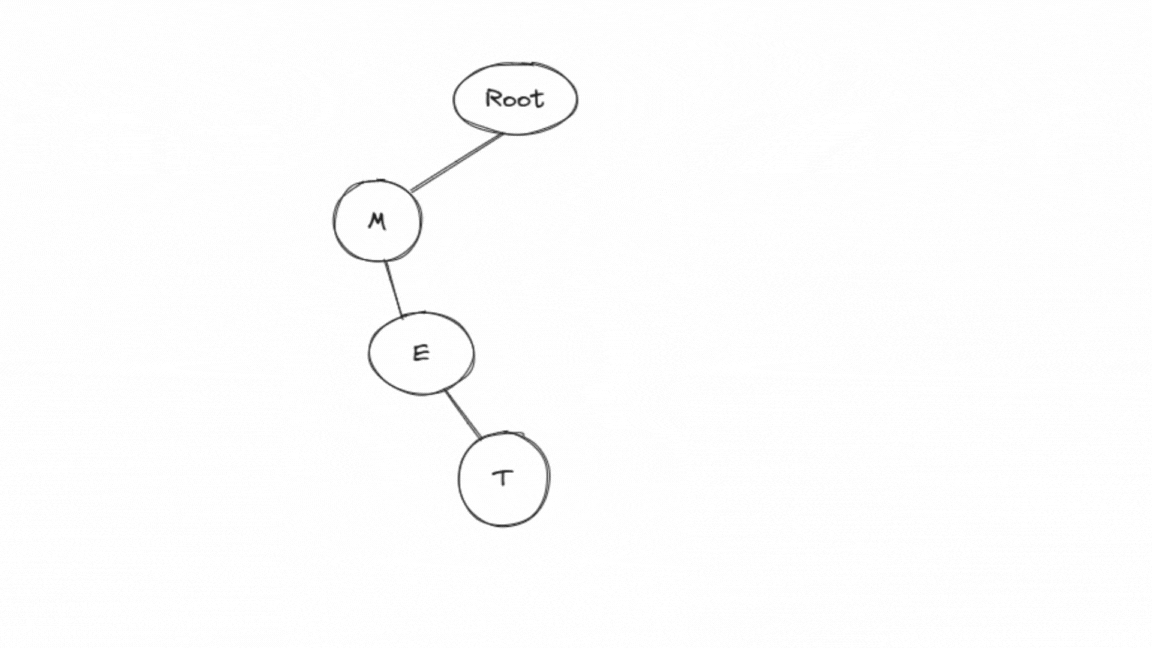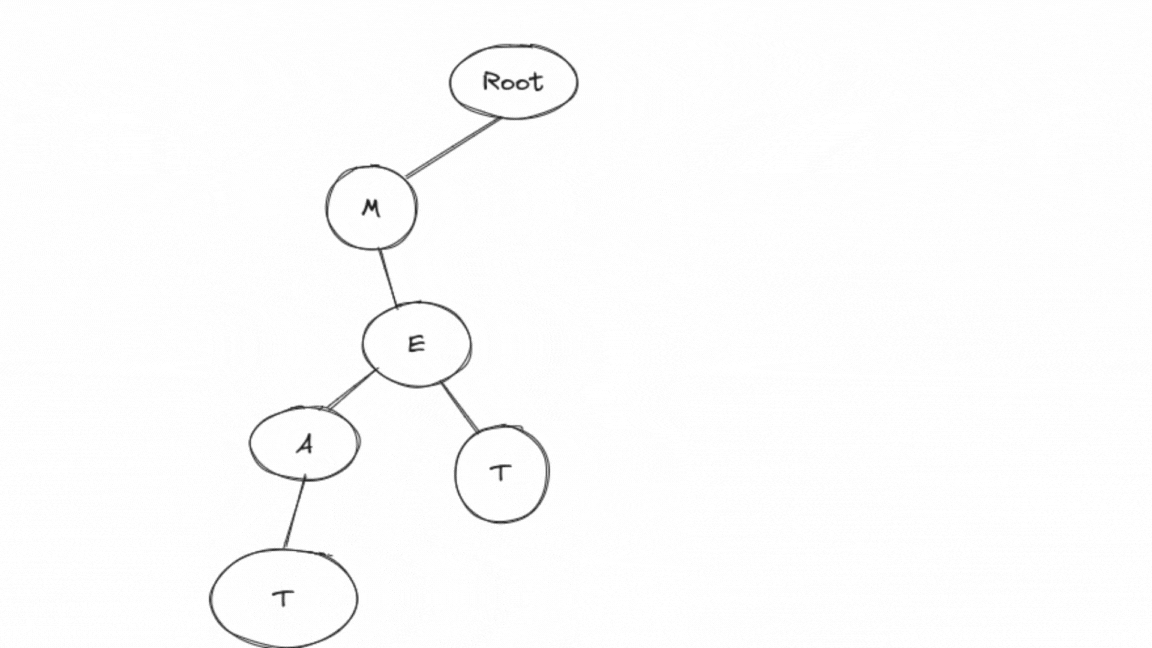

Search word in Trie:

The search function is used to check if a given word exists in the Trie.
It takes a single argument, word, which is the word we to search for in the Trie.
Inside the search function, it calls the searchtnode function, passing the root of the Trie (starting from the root of the Trie) and the word to search for.
The searchtnode function is responsible for traversing the Trie to check if the word exists.
It initializes cur as a pointer to the root of the Trie.
Then, it iterates through each character of the word.
For each character in the word, it calculates the index corresponding to that character by subtracting 'A' from the character, which gives the position in the children vector.
If at any point during the traversal, it encounters a NULL child node for the calculated index, it returns false, indicating that the word is not present in the Trie.
If it successfully traverses the entire word and reaches the last character, it checks if the isTerminal flag of the current node is set to true. If it is, it means the word exists in the Trie, and it returns true. Otherwise, it returns false.

Here's a step-by-step explanation of how the search function works:

In the main function, the word "MET" and "MEAT" are inserted into the Trie using the insert function.
Then, the search function is called with the word "MET."
Inside the search function, searchtnode is called with the root of the Trie and "MET."
The function starts from the root and traverses the Trie as follows:
1. 'M' exists as a child of the root.
2. 'E' exists as a child of 'M.'
3. Since 'T' is a terminal node, the function returns true.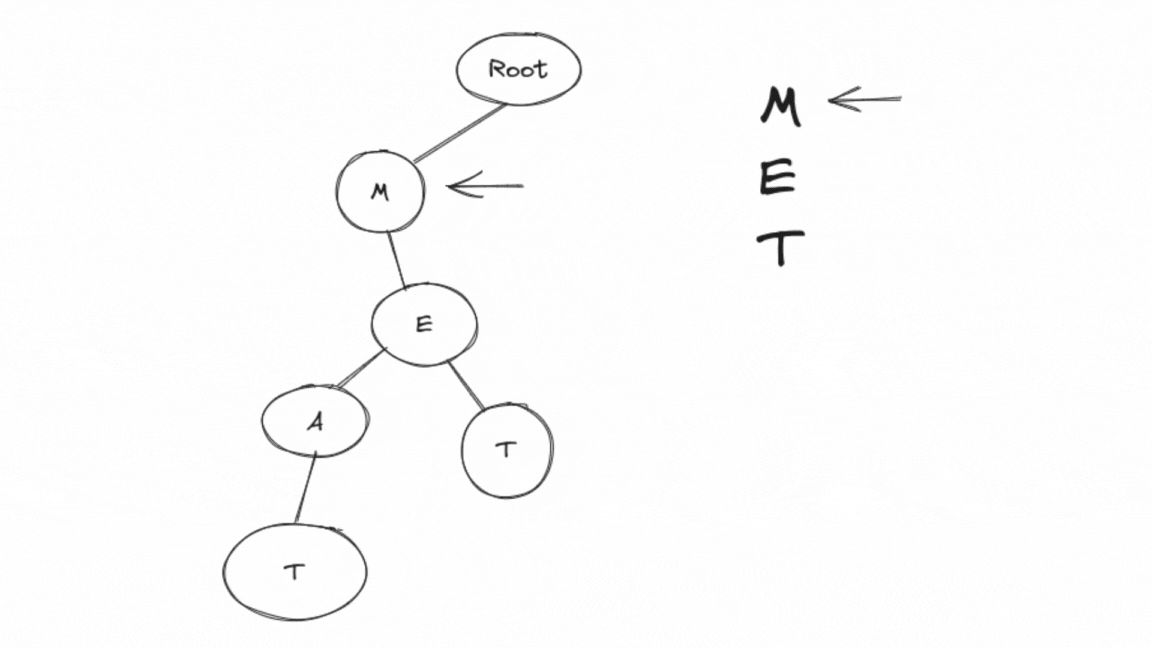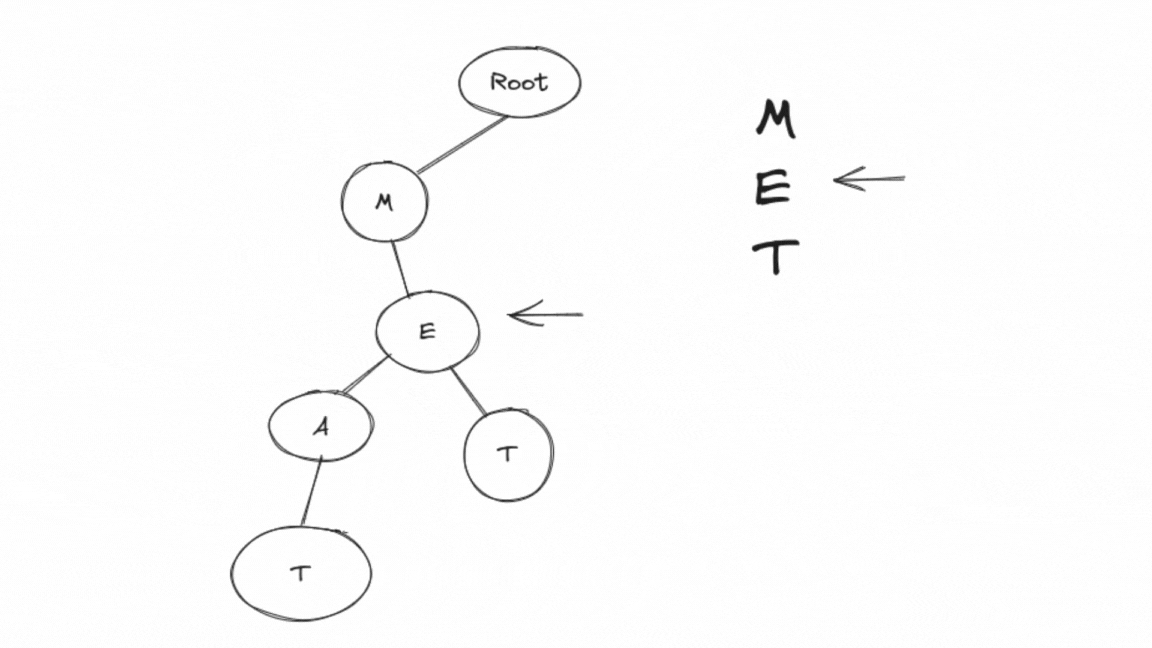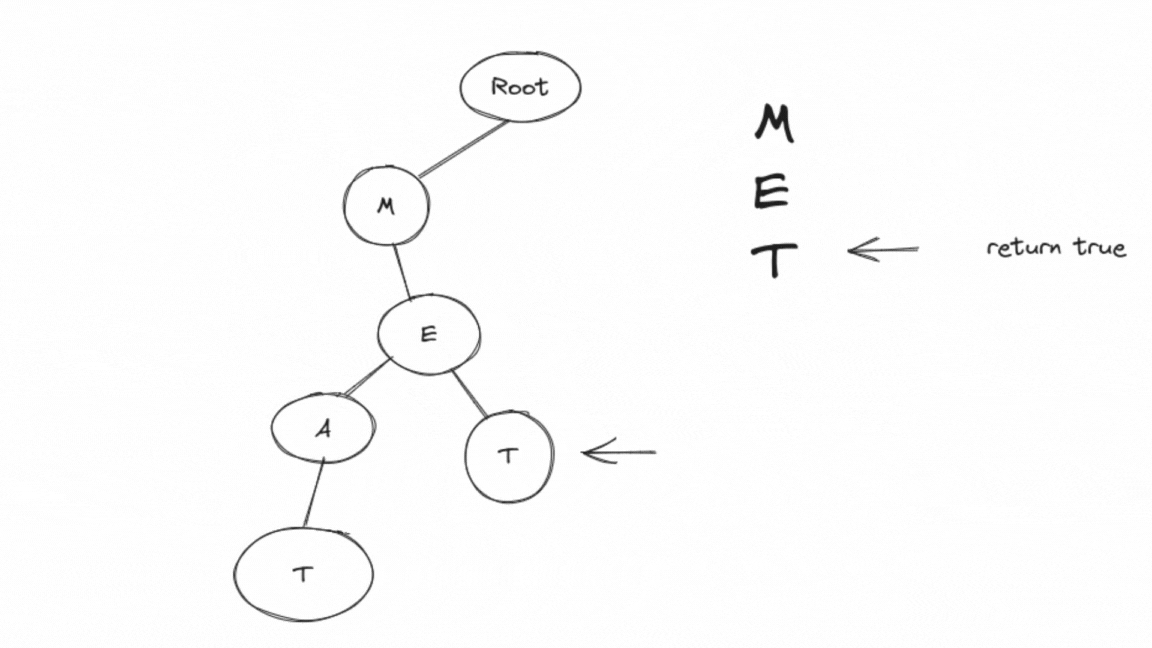

Remove word in Trie:

It starts at the root node and traverses the Trie character by character to find the word to be removed.
If the word is found in the Trie ( each character exists in the Trie), it marks the last node as non-terminal (removing the association of that node with the end of a word).
If the Trie contains the word and the last node is marked as non-terminal, it returns true to indicate that the word was successfully removed.
If the Trie does not contain the word (at any point, a character is not found), it returns false to indicate that the word doesn't exist in the Trie . Now, to remove "MET" from the Trie,

Mark the 'T' node as a non-terminal node by setting isTerminal to false, indicating that "MET" is no longer a complete word.

Application of Trie

Autocomplete and Predictive Text: Tries are widely used in search engines, text editors, and mobile keyboards to provide autocomplete suggestions as users type. They quickly offer a list of possible word completions based on the input prefix.
Spell Checking: Tries are essential in spell-checking algorithms. They can quickly determine if a word is correctly spelled or suggest alternative spellings when a word is misspelled.
Contact Management: Contact management applications use Tries to quickly search for contacts based on name prefixes, enhancing user experience in smartphones and email clients.
Dictionary and Word Games: Tries are used in word games like Scrabble and crossword puzzles. They enable efficient word lookup, word validation, and word formation.
IP Routing: In networking, Tries are employed to store and retrieve routing information for IP addresses. Routers and switches use Tries to determine the best path for data packets.
URL Routing: Tries can be used for URL routing in web applications, mapping URLs to specific resources or controllers. This ensures that the application can efficiently handle incoming requests.
Compression Algorithms: Tries can be utilized in compression algorithms like Huffman coding, where they help represent variable-length codes efficiently.
Genomics and Bioinformatics: Tries are used for DNA sequence alignment and searching for patterns in genetic data.
Natural Language Processing (NLP): In NLP tasks such as sentiment analysis, topic modeling, and language modeling, Tries can be used to efficiently search for and process words and phrases.
Software Engineering: Tries can be used in code completion and code analysis tools to provide suggestions and identify code patterns.
Caching: Tries can be used in caching systems for fast retrieval of cached data associated with URLs or keys.

File Systems: Some file systems use Tries to organize and search for files and directories efficiently.

conclusion

In summary, Trie data structures provide efficient solutions for various real-world tasks involving strings and words. They excel at handling common prefixes and performing quick string operations. They find applications in diverse fields like text processing, networking, genomics, and gaming.

Whether you're using a smartphone, playing word games, or building a powerful search engine, Tries play a crucial role in enhancing user experiences and optimizing data management. Their efficient use of space and versatility make them valuable in modern computing.

As you explore data structures and algorithms, consider adding Tries to your toolbox. With their tree-like structure and dynamic capabilities, Tries offer elegant solutions to complex string challenges.

We hope this introduction to Tries has illuminated their significance in computer science and software development. As you dive deeper into these fields, remember the Trie—a potent tool for efficient string operations.

Happy coding and Trie adventures!

Unraveling the Power of Tries: A Trie-tastic Journey into Efficient String Operations

Table of contents