My Short Story <3

✨ This year, I've participated in the e-Yantra, IIT Bombay competition and have been allotted "Luminosity Drone" as the theme. One of the recent tasks was to create a PID controller for a drone in ROS, which was being simulated in Gazebo.

✨ We were expected to create the controller for a quadcopter and make it stable at the goal position as fast as possible. The allowed error was ± 0.2 in all the coordinates.

✨ Creating the controller was fun, but tuning it was not 😭. I spent days, trying to find the correct values of gains for every axis (roll, pitch, throttle). As this was my first time working with a PID controller, I decided to go for the trial-and-error method for tuning. I've seen many people struggle to stabilize the drone under the given limits in the discussion forum of this competition. So, I'll be sharing my experience and some tips to save some of your time <3

Creating and Tuning the Controller

1️⃣ First, we'll need to find the error, i.e., the difference between the current position of the drone and the goal position.

⭐ Error = Current position - Goal Position

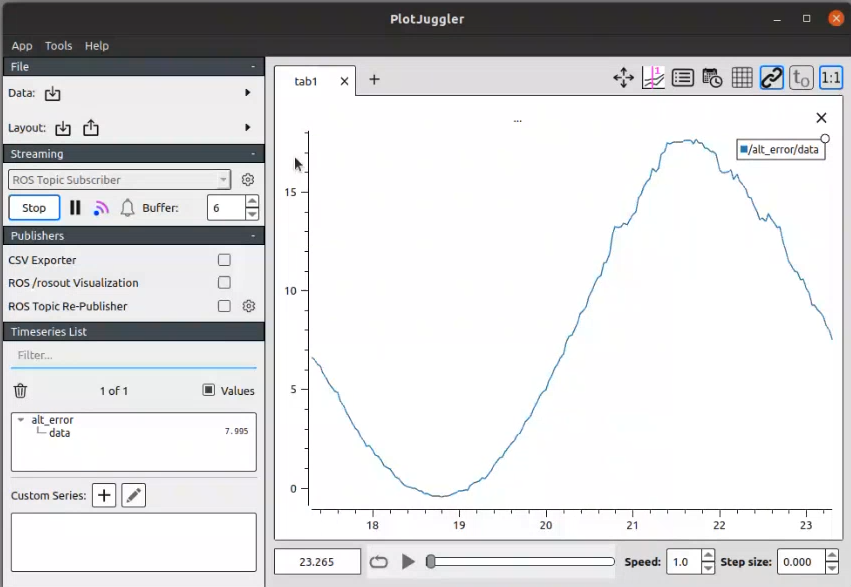
2️⃣ Now, we'll start increasing the value of Kp (proportional component). This will result in the drone, oscillating around the goal coordinates. Increasing the value of Kp will lead to the drone reaching the goal faster but making it too high will lead to instability.

📝 Increasing Kp for faster response but with the risk of instability.
⭐ Proportional Error = Kp *error

3️⃣ Next, our goal is to dampen those oscillations. So, we will start increasing the value of Kd (derivative component). This will result in dampened oscillations and reduced overshooting.

📝 Increasing Kd for dampened oscillations and reduced overshooting.
⭐ Derivative Error = Kd* (error - previous error)

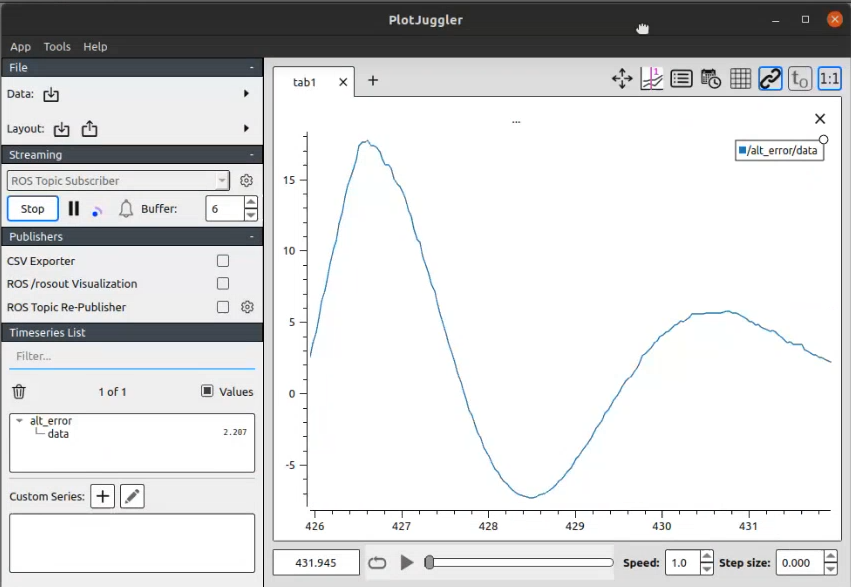
You'll notice that the drone is now hovering near the goal, but there's a difference in the current position of the drone and the goal. This difference is known as steady-state error.

4️⃣ To get rid of this error, we'll increase the values of Ki (integral component). This will result in our drone hovering even closer to the goal than before. A very high value of Ki can introduce instability and make the drone oscillate.

📝 Increasing Ki to eliminate the steady-state error but with the risk of potential instability.
⭐ Integral Error = Ki * (error + sum of errors)

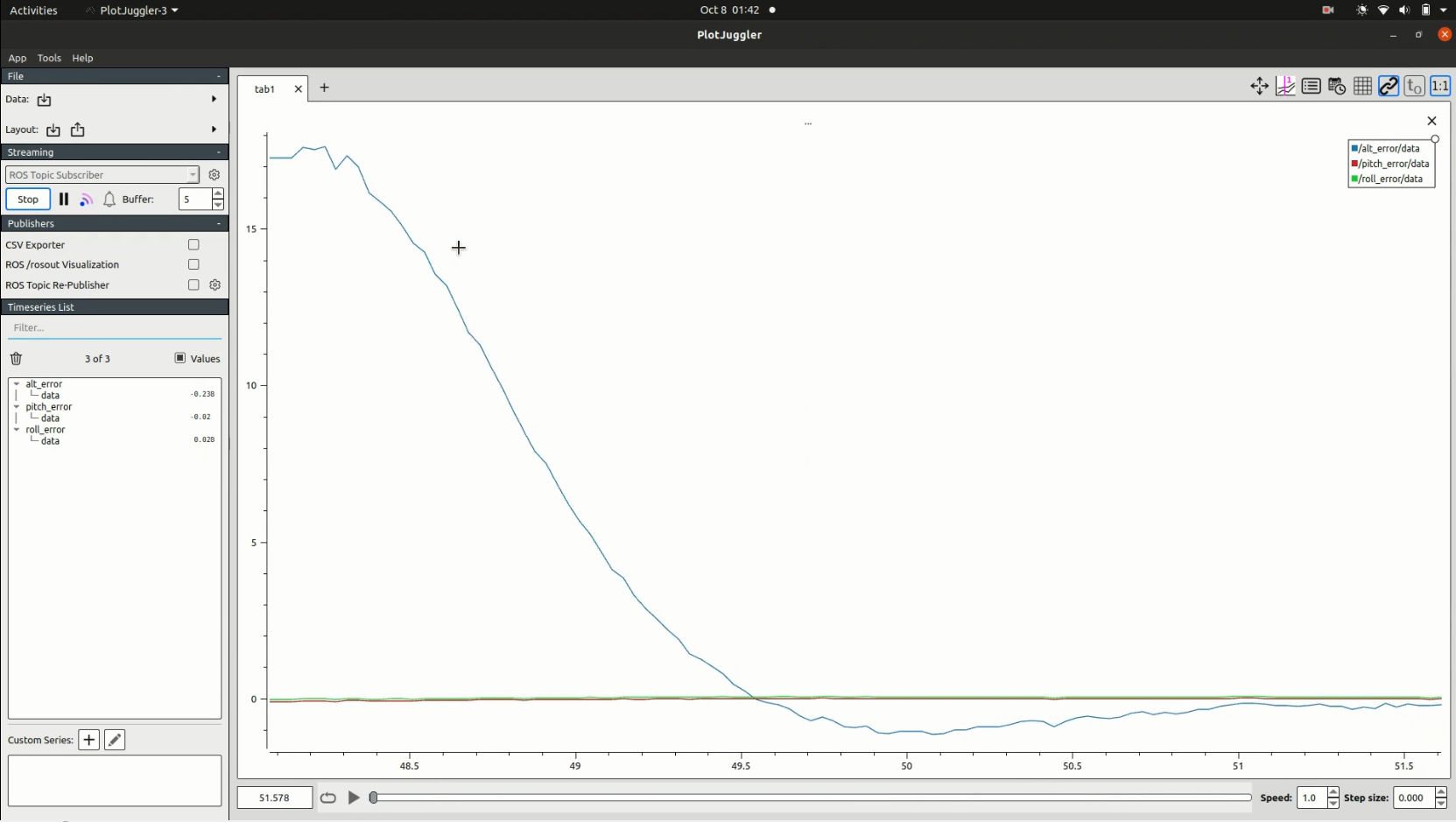
✨ Output = Proportional error ± Derivative error ± Integral error

Note: Do experiment with those ± signs in the output according to your requirements. Keep in mind that the choice of these signs can have a significant impact on the behavior of your system.

Happy Ending :)

I managed to score 50/50 on this task (felt very proud :')) and learned a lot about PID controllers in general. All these tips are very similar to the Ziegler–Nichols method and sound like a better way to find the values of the gains instead of blindly guessing them :)