Searching Algorithms
 Fatima
FatimaTable of contents

Search algorithms are in high demand to handle complex programs and ever-increasing volumes of data. Learning about these search techniques is essential, as it can help us improve the performance and organization of our programs.
In this article, we will explore the fundamentals of search algorithms to make our code more efficient and organized.
Types of Search Algorithms
Let's explore search algorithms in more detail. Just as you wouldn't use a dictionary to find a specific word in a book, you need to choose the right search algorithm for the problem at hand. In this section, we'll introduce two commonly used search algorithms, linear search and binary search. and we’ll explain when and where to use each.
Linear Search
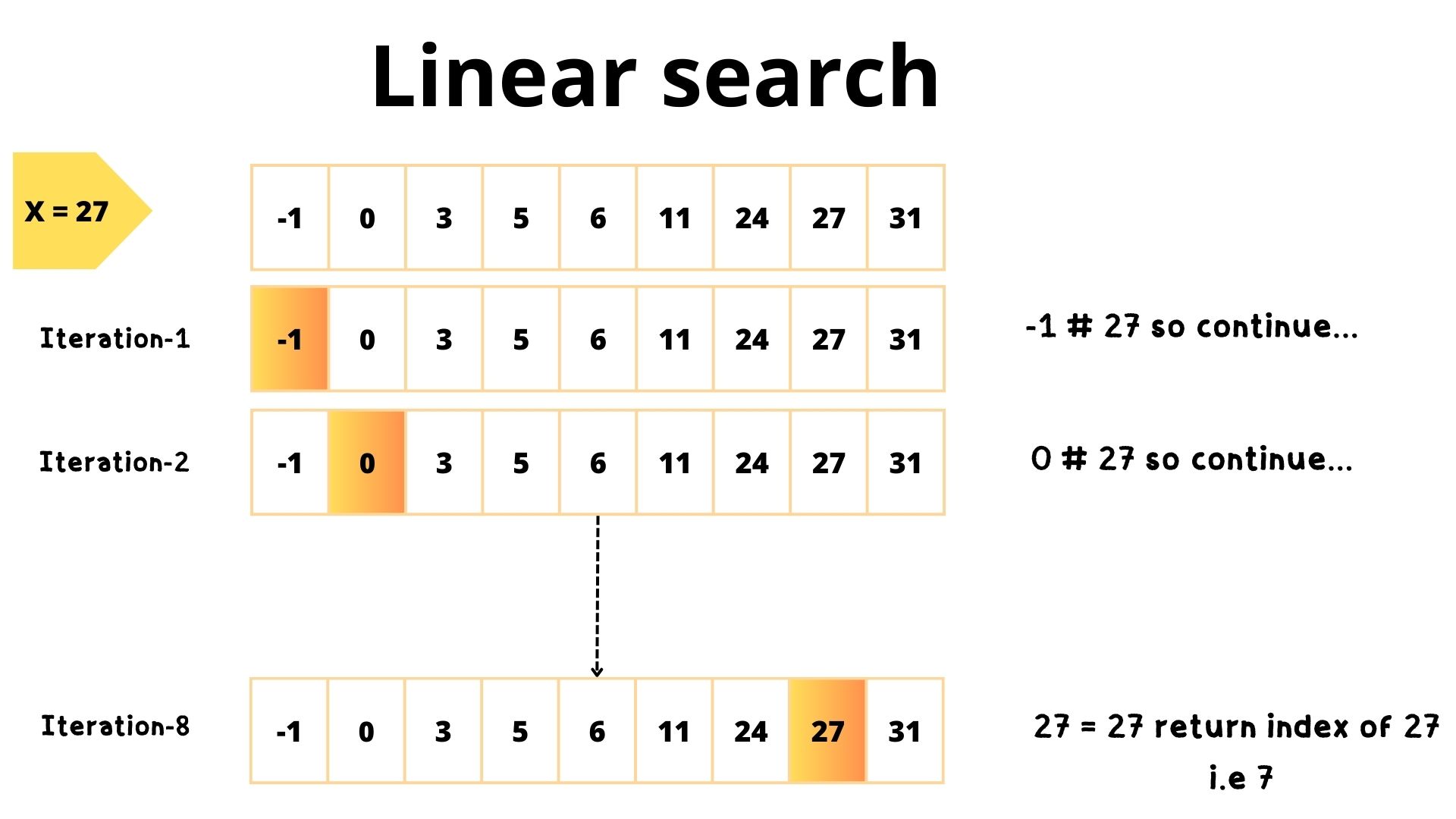
A linear search or sequential search, is one of the simplest search algorithms. It’s like searching for lost keys in your house by checking every room, one by one. In programming, a linear search goes through a list item by item.
Pseudocode:
def linear_search(collection, target):
for i in range(len(collection)):
if collection[i] == target:
return i
return -1
Time and space complexity:
| Best case | Average case | Worst case | |
| Time Complexity | O(1) | O(n/2) | O(n) |
| Space Complexity | O(1) | O(1) | O(1) |
code:
public class LinearSearch {
public static int linearSearch(int[] arr, int target) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == target) {
return i;
}
}
return -1;
}
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -1
Linear search is effective for smaller collections, but it can be inefficient for large collections. This is because it needs to compare every element to the target.
Binary Search
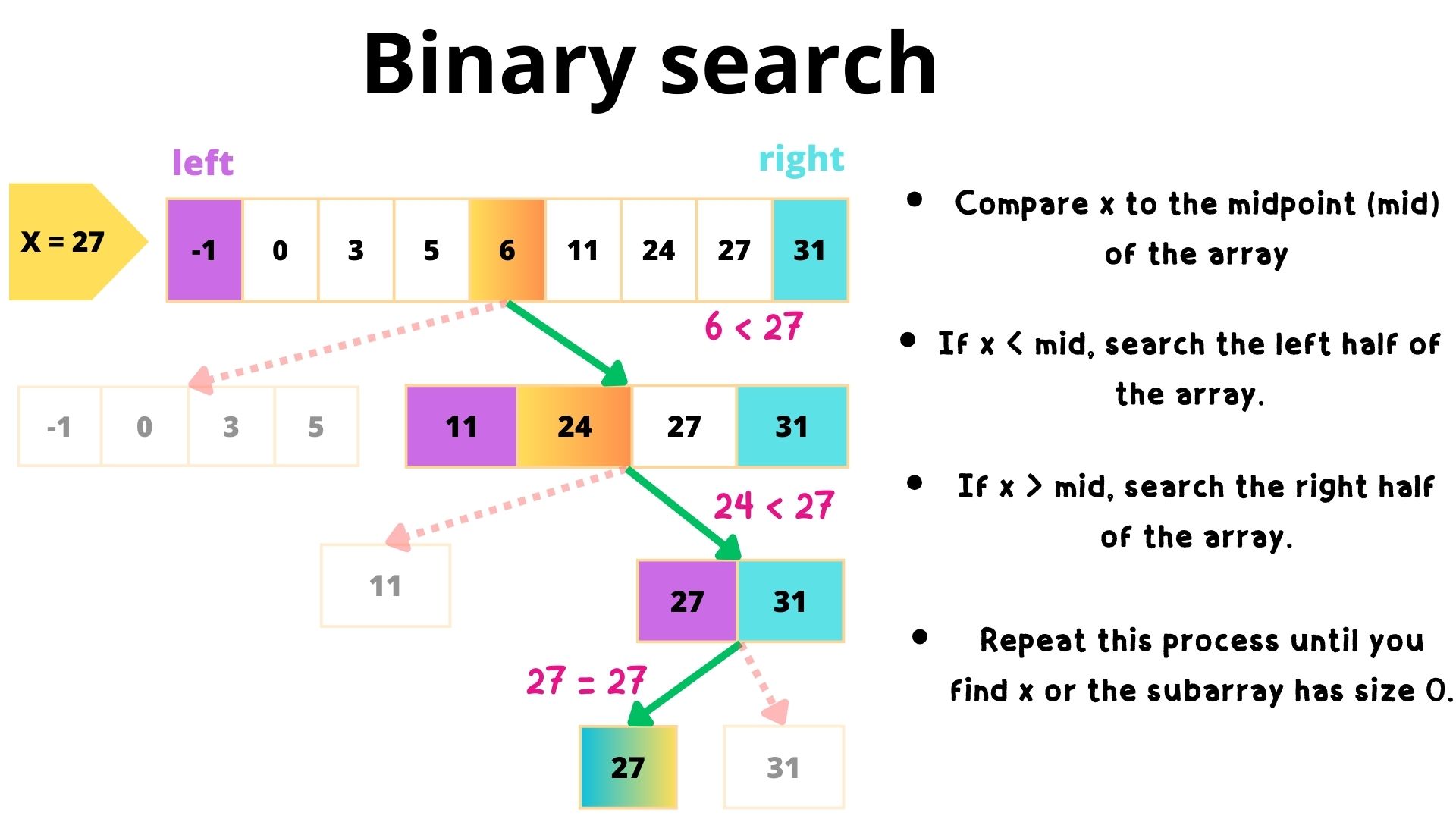
Binary search is a super-efficient way to find a target element in a sorted list. It works by dividing the search area in half, checking if the item is in the first or second half, and repeating this process until the target element is found.
Pseudocode:
def binary_search(collection, target):
low = 0
high = len(collection) - 1
while low <= high:
mid = (low + high) // 2
if collection[mid] == target:
return mid
elif collection[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1
Time and space complexity:
| Best case | Average case | Worst case | |
| Time Complexity | O(1) | O(log n) | O(log n) |
| Space Complexity | O(1) | O(1) | O(1) |
Code:
public class BinarySearch {
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2; // Calculate the middle index
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
}
def binary_search(arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
Conclusion
The choice of linear search or binary search depends on the specific context, where linear search is simpler to implement, while binary search is more efficient.
| Linear Search | Binary Search | |
| Definition | Check each element in order | Divides and checks the middle element iteratively |
| Requirements | None | Sorted Collection |
| Use Cases | Small datasets or unsorted data | Large and sorted datasets |
| Efficiency | O(n) | O(log n) |
Subscribe to my newsletter
Read articles from Fatima directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
