Recursion Problems

Hello everyone, I hope that you all are doing great and being wary of the weather changes. So, today it's my day 4 since my 100-day DSA challenge began. Till now we discussed a few things like time complexity, space complexity and recursion. But I don't think that what you study is complete until or unless you try to implement those things to solve a problem.

In our last discussion, we discussed what is recursion and what are the types of recursion and the conditions that need to be fulfilled while implementing recursion. So, for today we will be solving 2-3 recursion basic recursion problems. The problems that we're Factorial of a number, Fibonacci series and Ackermann function. Do these three problems feel like you have heard somewhere around in mathematics? If yes, then you're halfway there to solving the recursive function. The concept used to create programs of such topics in any language like C++, etc. is the same as the concept you understood from your mathematics teacher.

• Factorial of a number\= It's calculated by multiplying every number starting from 1 till the number itself. Example: 5! = 5x4x3x2x1 = 120.

int factorial(int number){
         if(number==0 || number==1){
              return 1;
         }
         else{
              return number*factorial(number-1);
         }
}

• Fibonacci Series = The sum of the last two numbers is called the Fibonacci answer of the number.

    int fibonacci(int number){
             if(number<=1){
                  return number;
             }
             else{
                  return (fibonacci(number-1) + fibonacci(number-2));
             }
    }
  

  • Ackermann function = It's a function with two arguments each of which can be assigned any non-negative value.

    Let m and n be two non-negative integers: -

    

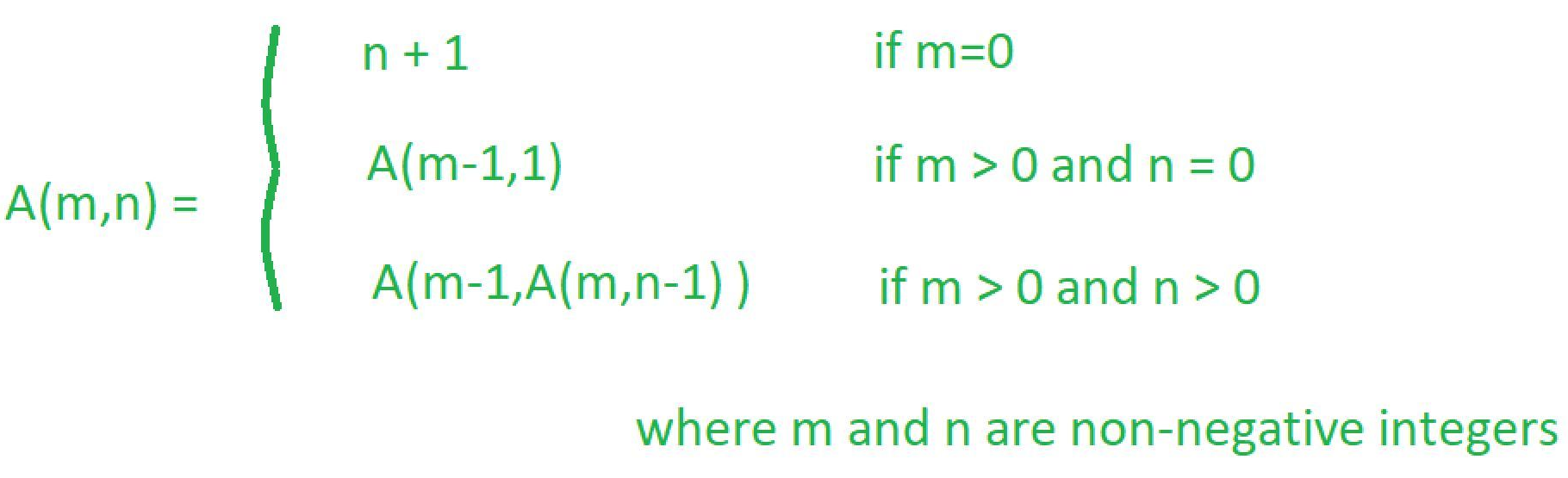
      int ackermann(int m, int n){
               if(m==0){
                   return (n+1);
               }
               else if( m!=0 && n==0){
                   return ackermann(m-1,1);
               }
               else{
                   return ackermann(m-1,ackermann(m,n-1));
               }
      }