Generating Synthetic Bank Transactional Data Using Markov Models 🏦

🏦 Simulating Bank Transactions with Hidden Markov Models 🔄

The generation of realistic synthetic bank transaction data is essential for various fields like machine learning, fraud detection, and software testing, without compromising customer privacy. Hidden Markov Models (HMM) present an innovative approach, leveraging sequential data patterns to mimic transaction behaviors. 🛠️✨

🔍 Problem Statement:

Banks and financial institutions are constantly in search of methods to create synthetic transactional datasets that mirror the characteristics and intricacies of real-world data. This is where our focus lies. We aim to generate a synthetic dataset with the following features:

1. customer_name: A unique identifier for every customer.

2. account_name: The account details associated with the customer.

3. profile: A categorization of the customer’s banking behavior. Examples include regular savings, high-frequency trading, consistent bill payments, etc.

4. transaction_type: Specifies whether the transaction was a deposit or withdrawal.

5. Amount (USD): The value of the transaction in U.S. dollars.

6. time_transaction: The timestamp of when the transaction took place.

7. transaction_city: The city where the transaction occurred.

8. transaction_category: The category of the transaction (e.g., groceries, utilities, entertainment).

9. transaction_ref_id: A unique reference ID for each transaction.

Before delving into the details, let’s understand the Hidden Markov Model.

📜 Understanding Hidden Markov Models (HMM) 🧐

Hidden Markov Models (HMM) depict systems with unseen states influencing observed results. Here’s a quick breakdown for our banking scenario:

• Hidden States:Customer’s banking behavior, like saving or spending habits.
  - Observable Emissions: Transactions, such as deposits or withdrawals.
  - Transition & Emission Probabilities:HMM uses probabilities for state transitions and resulting transactions.

Using HMM, we’ll craft a synthetic dataset mirroring real bank transactions.

Note: This article won’t delve deep into the intricacies of the Markov model. Our focus is squarely on leveraging HMM to craft synthetic bank data.

Let’s assume:

1. Profiles as Hidden States:

• Saver: Skewed towards deposits with fewer transactions.

• Spender: Often seen making withdrawals.

• Regular Biller: Steady cadence, likely monthly transactions.

• Erratic: Totally unpredictable.

1. Transaction Types as Observable States: Given a profile, our primary observable hint is the ‘transaction_type’. Let’s decode the link between profiles and transactions! 🗺️📈

Transition and Emission Probabilities Unpacked 📊

• Transition Probabilities: Dictate how customers shift between profiles. For instance, a ‘spender’ might transform into a ‘saver’ after big expenses.

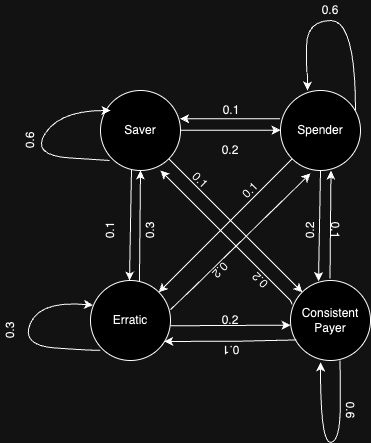
In the transition matrix:

- Row 1 (Saver): Indicates the probabilities for a customer currently classified as a ‘Saver’ to transition to other profiles. For instance, the values [0.6, 0.2, 0.1, 0.1] suggest that a ‘Saver’ has a 60% chance to remain in the same profile, a 20% chance to shift to a ‘Spender’, 10% to a ‘Consistent Payer’, and 10% to an ‘Erratic’ profile.

This matrix encapsulates the likelihood of a customer’s profile transition to different states in the subsequent time step.

- Emission Probabilities: Profile-based likelihoods. A ‘saver’ is more inclined to deposit than withdraw.

The emission probabilities matrix details the probabilities of observing specific transaction types given a customer’s profile. For instance:

- Row 1 (Saver): The values [0.8, 0.2] suggest that a ‘Saver’ profile has an 80% chance of emitting a ‘deposit’ and a 20% chance of emitting a ‘withdrawal’ in a transaction.
- Similarly, for ‘Spender’, there’s a 30% probability of emitting a ‘deposit’ and a 70% probability of emitting a ‘withdrawal’.

This matrix guides the likelihood of transaction types based on a customer’s profile, assisting in generating synthetic transactional data using HMM.

Understanding the Implementation of Synthetic Bank Data Generation

Initiating the Hidden Markov Model with Customer Profiles:

The core foundation of our synthetic data generation is the Hidden Markov Model (HMM), where we define customer profiles as hidden states.

• We initiate the HMM using the MultinomialHMM from the hmmlearn package.

• We specify the number of hidden states using n_components (which is the number of customer profiles).

• We initialize the starting probability to be equal for all profiles.

• We then set the transition and emission probabilities for our HMM.

2. Generating Transactions for Multiple Customers:

For each customer, a series of transactions are generated based on their profiles and the underlying HMM probabilities.

• We use the Faker library to generate synthetic yet realistic names and account numbers.

• model.sample(transactions_per_customer) is used to generate a sequence of profiles for each customer.

• Each profile corresponds to a specific behavior like ‘Saver’ or ‘Spender’, guiding the subsequent transaction’s nature.

Once the profile sequence is obtained, transaction details are determined based on the profile’s emission probabilities.

• Chooses a transaction type (either ‘withdrawal’ or ‘deposit’) based on the emission probabilities associated with the current profile.

• Further transaction details like amount, time, city, and category are then generated using a mix of random choices and the Faker library.

After generating transactions for all customers, the data is structured in a Pandas DataFrame and saved as a CSV file 🚀

Now, let’s visualise the distribution of customer profiles over different time frames. This helps validate the synthetic data’s accuracy and provides insights into how profiles are distributed among customers across various points in time 📈.

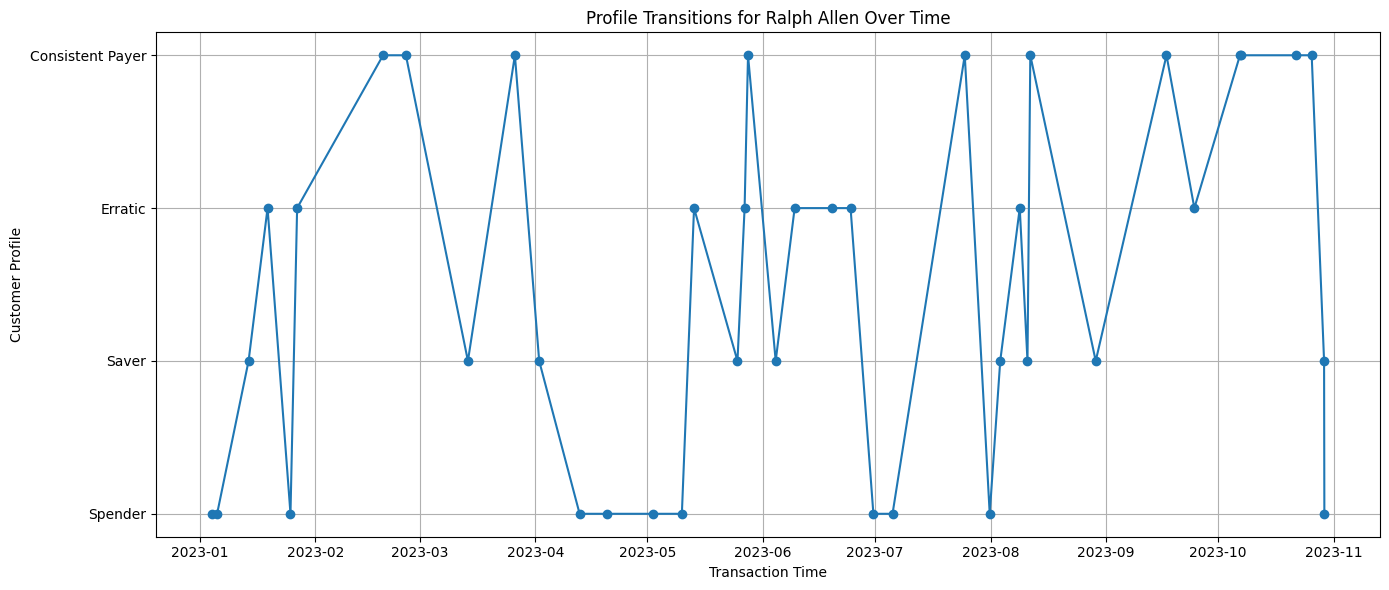
Conclusion

Through the use of Hidden Markov Models, we’ve illuminated a pathway to generate synthetic bank transactional data. Such methods hold value in realms like testing and AI training, ensuring data privacy. Tools like hmmlearn and Faker amplify this capability.

Thank you for accompanying us on this journey. Until the next exploration! 😃

GitHub

Warning: Portions of this article were assisted by ChatGPT 🤖 . All content has been reviewed and edited by human oversight.*

Reference Links: