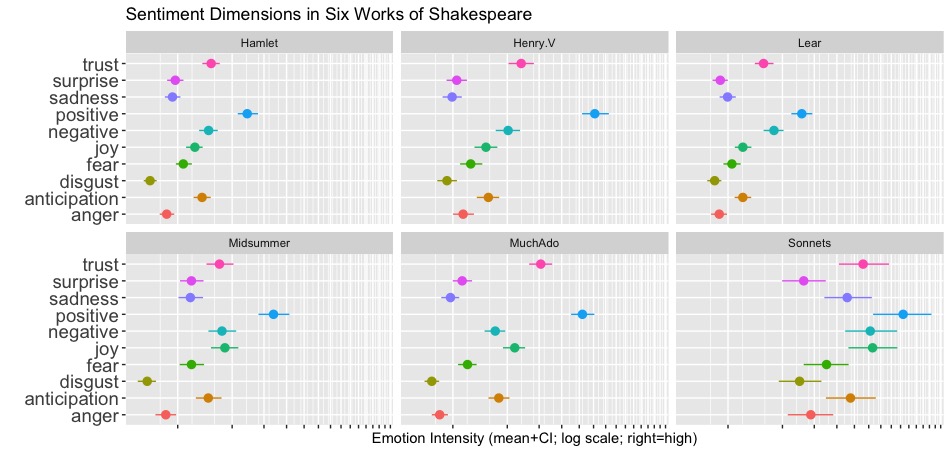
Previously, Part 1 of this post demonstrated how to score open-end text comments on 10 emotional dimensions in R. Such multidimensional sentiment analysis (MDSA) is a scalable, automated way to reveal much more than common unidimensional sentiment analysis.

In this post, we'll see how this may be extended to multiple products and used to cluster them. In product categories with multiple competitors, this can reveal which competitors are most similar to your product in emotional perception. You can also find out which ones are most differentiated, which ones are most similar to one another, and so forth. That can help you focus attention on the competitors who matter the most — either because they are near neighbors or are perceived quite differently.

To get there, we'll first look at very common multivariable analyses: a correlation matrix and exploratory factor analysis (EFA). Those will be familiar to many readers (or check the R book or Python book for details). Then we look at a more unique approach, using composite perceptual maps (CPM).

Setting It Up

As noted in Part 1 (read it before this post), I'm using text from six works by Shakespeare, pretending that each work is a "product" (in fact, they were products for Shakespeare; and still are for repertory theaters). The actors' lines in the works are a proxy for "comments" as if users reported them in reviews or other feedback. When we have code that works for multiple plays, scoring their lines, it will also work for multiple products and scoring their comments.

To get the data, I recommend you read through the blog Part 1, and use the code there to acquire and score the texts. But, to save you some time, I've uploaded the final scores to the Quant UX book's website. If you prefer, you can skip the code in Part 1 (but read it for background) and use R to download the final data directly:

## Load coded sentiment data, from blog part 1
## https://quantuxblog.com/multidimensional-sentiment-analysis-part-1
shake.sent <- readRDS(url("https://quantuxbook.com/misc/shakespeare-sentiment.Rds"))
head(shake.sent)

In R, the head() should match these first 6 lines of multidimensional emotion codings:

Side point. For readers of part 1, there is an addition I made along the way — not relevant to the blog posts — and that is calculating net sentiment scores (the SentScore column). For completeness, that was calculated by summing up the 5 positive direction columns, and subtracting the 5 negative columns, as follows:

shake.sent$SentScore <- rowSums(shake.sent[ , c("anticipation","joy","positive","surprise","trust")]) - 
                        rowSums(shake.sent[ , c("anger", "disgust", "fear", "negative", "sadness")])

Next, we'll see how traditional correlation analysis can be used on these data.

Correlations

The first thing we could examine is the correlation matrix. If a comment (or, in this case, a line from Shakespeare) shows one emotion, how likely is it to show some other emotion?

I use the cor() function to find the correlation matrix, and then corrplot.mixed() from the corrplot package to visualize the matrix. I remove the names of the works (as text, they don't correlate) and I also remove the overall sentiment score (as a calculation of the other columns, its correlation is not very interesting).

library(corrplot) # install if needed
corrplot.mixed(cor(shake.sent[ , c(-11, -12)]),  # -11 to remove name of the work, -12 to remove sum
               upper="ellipse", 
               upper.col=colorRampPalette(c("red","lightgoldenrod","darkblue"))(200),
               lower.col=colorRampPalette(c("red","lightgoldenrod","darkblue"))(200),
               tl.cex=1, tl.pos="lt", diag="u",
               number.cex=0.8, 
               order="hclust")

Lines 3 to 8 are not required but they improve the plot; I won't detail them (see Section 4.5 of the R book).

Here's the resulting correlation matrix plot:

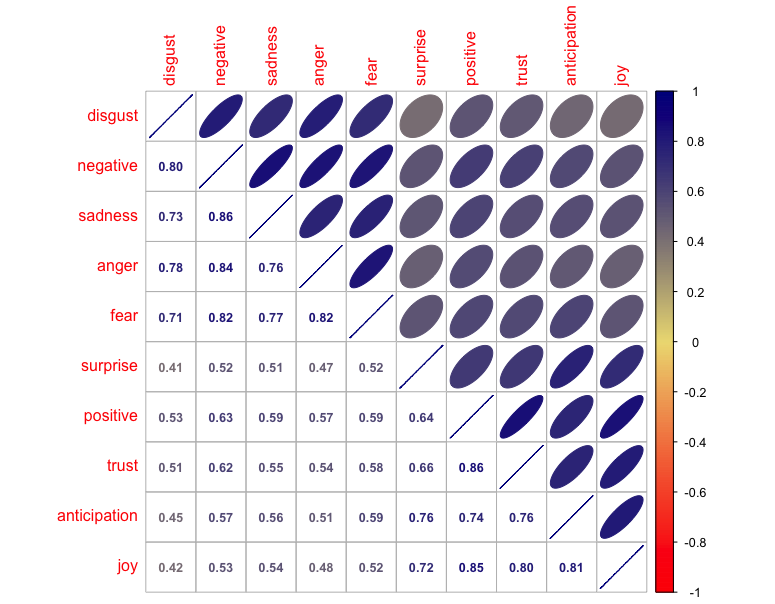
A couple of features stand out. First, everything is positively correlated! That surprises me every time. We might expect that positive and negative comments would occur separately, such that a comment with positive words would tend to have fewer negative words. But there is a confounding effect here: longer comments tend to have higher frequencies of all words and thus more positive and negative words. That can be important for analysis, but we can't go into every issue in depth here. I just wanted to note it.

Second, the positive words and negative words do co-occur with one another at a higher rate (around r=0.7) than the baseline rates (r=0.55 or so). So, although everything is positively correlated, there are recognizable and expected patterns.

Correlation matrices are important to review but are far from the end goal. Next, we'll look at factor analysis.

Factor Analysis

Factor analysis is a huge area (see Chapter 8 of the R book or Chapter 9 of the Python book), and I'll assume here that you're generally familiar with exploratory factor analysis (EFA). The goal of EFA is to reduce a set of variables — in this case, the emotion scores — to a smaller set of underlying latent factors that explain observed patterns in the larger set. (EFA attempts to find factors that will recreate the observed correlation matrix, as above, except using many fewer variables.)

Given our scored sentiment data, we can ready to dive into EFA. Here's an example 4-factor solution. (I'm not claiming that 4 factors is the best solution, only that it is an interesting solution.)

library(GPArotation)  # install if needed
factanal(shake.sent[ , c(-11, -12)], factors=4, rotation = "oblimin")

This code first loads the GPArotation package, which provides options to find correlated factors (in these data, we saw that everything is correlated). Then it uses base R factanal() to perform factor analysis (there are other options such as the psych package). As before, it omits the names of the products (column 11) and the computed net sentiment score (column 12). It looks for a solution with 4 factors and uses an oblimin rotation that allows correlated factors (again, see the discussion of EFA in the R book or Python book for a detailed explanation).

Here's the result:

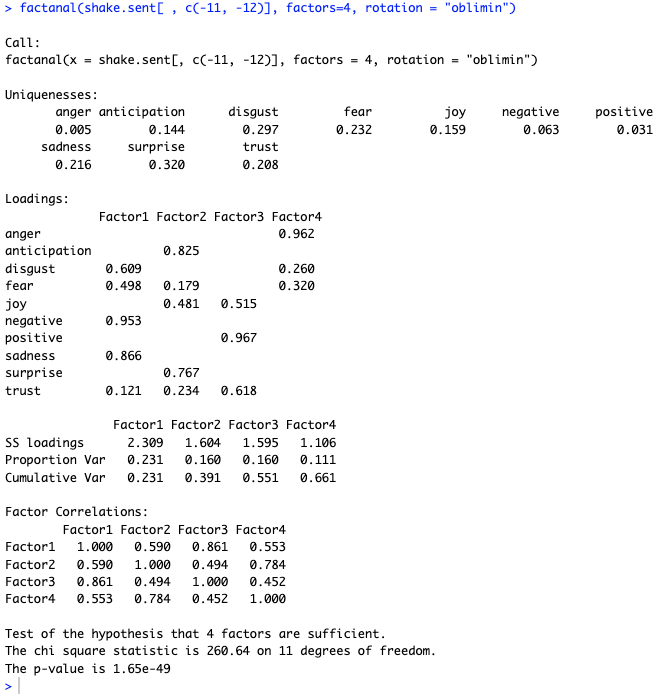
In this solution, the 4 factors are fairly distinct: there is a negative/sad factor (F1), an anticipation/surprise factor (F2), a generic positive factor (F3), and an anger factor (F4). The factors account for 66% of the observed, modeled variance in the data.

Finally, it gives a correlation matrix for the factors — and again we see that the factors are all positively correlated. Interestingly, Factor 1 (sadness) occurs more with Factor 3 (positive), r\=0.86, than it does with Factor 4 (anger), r\=0.55. Anger goes more with anticipation, r\=0.78. (Remember, those are not general statements; they reflect the emotions in these Shakespearean works, according to our coding.)

In practice, such analysis can be used to uncover patterns of how users are talking about products. And that's another step toward one of my favorite methods, which we'll see next.

Composite Perceptual Map

This is where the multidimensional scores become even more powerful.

The general concept of a composite perceptual map (CPM) is that it identifies the dimensions of relatively stronger and weaker perceptions of a product or whatever you're studying. (Multidimensional scaling is an alternative and similar approach.)

For example, we might know that Product A is overall a very strong brand, while Product B is relatively weaker across many dimensions. That doesn't help us identify what to do, because "overall strength" is not directly addressable by product design or branding strategy. Using CPM we can ask a much more specific question: relative to each product's average baseline, what are its strengths and weaknesses? It also answers this question: among the perceptions we measured, which dimensions are most important to distinguish the products?

In this case, let's look at the chart before the code. Following is a CPM chart for the 5 plays in our data set, using the 10 emotional dimensions.

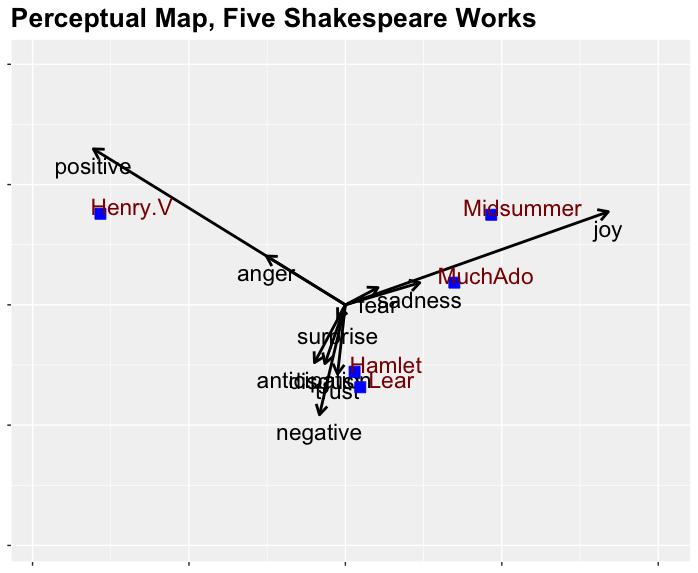
I'll decode a few aspects of this chart:

There are three key dimensions distinguishing the plays in their relative perception: positive + anger (upper left), joy + sadness (upper right), and a complex set of emotions including negative, trust, disgust, anticipation, and surprise.
We see the relative correlations of those three dimensions in the angles between the arrows. The closer they are, the higher the correlation. Perfectly negative correlation would show as a 180 degree angle, and perfectly positive correlation would be 0 degrees. Uncorrelated dimensions appear at 90 degrees. In this case, the three perceptual dimensions are modestly negatively correlated. This means that — relative to its baseline frequency of all emotions — to the extent that a play has, say, anger, it will be somewhat less likely to feature fear or disgust.
It identifies which products (plays) go together in perceptual space. For example, in terms of the underlying patterns of emotion, Lear and Hamlet are quite similar to one another and quite different from Henry V or Midsummer.

How would one use this for products? One way is to understand the competitive landscape and make strategic choices. Imagine that our product is Lear, while our key competitors are Hamlet and Henry V. We can see that Hamlet is perceived as being extremely similar to us in the emotional landscape, while Henry V is quite different. If we want to differentiate our product, this might lead us (for example) to move in a direction away from both of them. On the chart, that would involve emphasizing elements of joy, the strongest determining dimension in a different direction.

Another use is to understand how users think about the product space overall. For example, we see in the chart that relative perceptions of anger and generic positivity go together. We could then ask "why?", perhaps using qualitative research.

For more discussion and statistical explanation, I'll defer again to the R and Python books. One important note: the fact that CPM charts involve relative positions (using MANOVA analysis under the hood) often poses complications, such as the fact that a product could be strong overall on a dimension that is nevertheless a relative deficit. We say more about that in the books.

Here's the code for the chart above. Note that it requires a lengthy function cpm.plot() that I share in R Code Block 1 at the end of this post. I omit that here.

In this code, I make a copy of the data and retain only those rows (lines of the plays) that have some emotion (i.e., the sums of the 10 emotion dimensions are non-zero). Because the Sonnets have extremely high relative emotionality, I remove them to avoid distorting the plot. (As we mentioned above, in practice one might also consider some sort of normalization, depending on the exact problem at hand.)

Here's the code:

# set up the data
sent.ratings <- shake.sent[ , 1:11]   # just ratings + platform
# keep only the rows where there is some sentiment
sent.ratings <- sent.ratings[rowSums(sent.ratings[ , 1:10]) > 0, ]
# plot dimensions only, and excluding the Sonnets
p <- cpm.plot(subset(sent.ratings, Work  != "Sonnets"), 
              "Work", names(sent.ratings[1:10]),
              plot.scatter=FALSE, plot.CI=FALSE,
              offset=0.05, 
              plot.brands = TRUE, aspect.lock = TRUE,
              zoom.out = 0.3, rotate = 20, 
              title.main = "Perceptual Map, Five Shakespeare Works")
p

As a few other minor notes, the cpm.plot() function takes the following important inputs:

data.in: in this case, the sent.ratings with all of the works and dimensions
brand.ids: the column name of the identifiers for products (in this case, plays)
measure.vars: the names of the predictor dimensions (the emotions)

We tell it to plot the products themselves, and not just the dimensional landscape, using plot.brands=TRUE. It can also plot rectangular confidence intervals; those are turned off here with plot.CI=FALSE. The other arguments control a few other elements of the chart such as the title and whether to rotate it in the 2-dimensional plotting space to be more readable.

Conclusion

That's it! I hope you're inspired by this post and part 1. With this R code, you have the tools you need to examine emotional dimensions in product comments, reviews, and any other kind of generic open-ended text.

There is one final thing to know, and that involves the kind of data you need to do such an analysis. You need text sources with two features: moderately large size, on the order of at least hundreds and preferably thousands of comments per product, and with emotional words (so they can be scored).

For more reading, discussing more use cases, building on the same example, and including concerns such as dictionary quality and ethics, see an article I wrote for the Journal of Marketing, available here: https://journals.sagepub.com/doi/full/10.1177/0022242919886882

All the R Code

As usual, I'm sharing all the code for these analyses. You most likely will need to install a few packages as noted. See Part 1 for code to do the initial data processing.

Today's post is more complex than usual, so I'm breaking this into two parts. Code block 1 compiles functions needed for the composite perceptual map. Simply copy/paste these and source() them to be available. Then skip down to code block 2 for all of the analysis code as shown in the post.

Code Block 1: CPM Functions
Source these first, so they are available for code block 2.

########
######## CPM Routines follow
######## Source from here to end of file before using cpm.plot() above
########

# also available as an R package at https://github.com/cnchapman/choicetools
#
# CITATION:
# Chris Chapman, Eric Bahna, James Alford and Steven Ellis (2019). 
# choicetools: Tools for Choice Modeling, Conjoint Analysis, and MaxDiff 
# analysis of Best-Worst Surveys. R package version 0.0.0.9073.

###############################################
# cpm.plot()
#
# All CPM functions follow this point
###############################################
#
# Authors: James L. Alford, and Chris N. Chapman
# Author contact: Chris Chapman, cnchapman@gmail.com
#
# CITATION FOR cpm.plot().  Use the main citation, or this one as you prefer:
#   Alford, JL, and Chapman, CN. (2012). cpm.plot: composite product mapping 
#     for R. [Computer software, version 0.2]
#
# OVERVIEW
#   Takes input variables + vector of "brands" and produces a "composite product
#     map", showing how the brands are "positioned" relative to one another by 
#     the variables.
#   This is done by performing a MANOVA for [variables ~ brands] and extracting 
#     the canonical discriminant functions. 
# 
# EXAMPLE CODE: 
#   Suppose iris species are our "brands" and we examine their "positioning" 
#     with regards to the other predictor variables:
if (FALSE) {
  data(iris)
  cpm.plot(iris, "Species", names(iris)[1:4], zoom.out=10, 
           title.legend="Species")
  # the same thing rotated, in case you want a different orientation
  cpm.plot(iris, "Species", names(iris)[1:4], zoom.out=10, 
           title.legend="Species", rotate = 90) 
}


###############################################
# cpm.rotate()     :: utility function
#   rotates (X,Y) Cartesian point matrix around origin in 2d
#
# INPUT PARAMETERS
#   points         = 2-column (X,Y) matrix of Cartesian coordinates
#   rotate         = amount to rotate clockwise around origin, in degrees
# OUTPUT
#   matrix of rotated points rotated around the origin
# EXAMPLE
#   cpm.rotate(cbind(c(1,2,3), c(5,3,4)), 90)

cpm.rotate <- function(points, rotate) {
  if (ncol(points) != 2) {
    warning("Points could not be rotated; not Cartesian in cbind(X,Y) format.")
    return(points)
  } else {
    theta <- -1.0 * pi * rotate/180
    x.rot <- points[,1]*cos(theta) - points[,2]*sin(theta) 
    y.rot <- points[,1]*sin(theta) + points[,2]*cos(theta)
    points.rot <- cbind(x.rot, y.rot)
    return(points.rot)
  }
}

###############################################
# cpm.se()     :: utility function
#   standard error of the mean for a vector
#
cpm.se <- function(vec.in) {
  sqrt(var(vec.in) / length(vec.in))
}

###############################################
# cpm.plot()     :: Main Function
#
# INPUT PARAMETERS
#   data.in      = data
#   brand.ids    = name of column with factor to discriminate; must have >2 
#                    levels
#   measure.vars = names of columns with predictors of brand.id
#                  e.g. measure.vars = names(data.in)[2:4]
#   zoom.out     = scale factor for vectors from discriminant functions
#                  try values 0.5 - 10.0 to get the best looking chart
#   rotate       = amount of clockwise rotation for the chart (in degrees)
#   trim         = proportion of the range of measure.vars to exclude from plot
#   xdim         = which DA function to show on X-axis (of the #levels-1 
#                    discriminant functions)
#                  WARNING: only tested with X == DA function 1
#   ydim         = which DA function to show on Y-axis
#                  WARNING: only tested with Y == DA function 2
#   aspect.lock  = make chart rectangular? (X-axis same length as Y-axis)
#   coeffs       = use "std" (standardized) or "raw" DA coefficients?
#                  generally should use "std" for better interpretation
#                  WARNING: only tested with coeffs=="std". removed "raw" 
#                    function in version 0.2.
#   plot.brands  = include brands on the plot? (if not, just plot dimensions)
#   plot.CI      = plot confidence intervals around the brand means?
#   plot.scatter = plot individual responses?
#   offset       = offset to position of brand labels (multiplication factor; 
#                    may help with label overplot)
#   ci.width     = number of Z scores for confidence intervals (95% CI == 1.96)
#                    around the brand means
#   font.mult    = how much to scale the label font
#   title.main   = chart title
#   title.legend = label for the legend [placeholder, not currently used]
#   label.jitter = how much to jitter the brand labels
#
# RETURN VALUE
#   ggplot2 chart object (and it draws the chart upon return)
#
# EXAMPLE CALL
#   cpm.plot(iris, "Species", names(iris)[1:4], zoom.out=10,  
#            title.legend="Species")

cpm.plot <- function(data.in, brand.ids, measure.vars, 
                     zoom.out = 1, trim = 0.0, xdim = 1, ydim = 2, 
                     aspect.lock = TRUE, rotate = 0, coeffs = "std",
                     plot.brands = TRUE, plot.CI = FALSE, plot.scatter = TRUE,
                     offset = 1.0, ci.width = 1.96, font.mult=1,
                     title.main = "Perceptual Map", title.legend = "Brands",
                     label.jitter = 0) {

  require(grid)      # for arrow functionality
  require(ggplot2)   # for plots
  require(candisc)   # for discriminant extraction

  # extract needed data from larger DF and remove NAs
  data.use <- na.omit(data.in[ ,c(brand.ids, measure.vars) ])

  # core discrimination model
  manova.out <- manova( as.matrix(data.use[ ,measure.vars]) ~ 
                          factor(data.use[ ,brand.ids]), data=data.use)

  # extract the discriminant functions. don't change! it seems very finicky
  candisc.obj <- candisc(manova.out, term="factor(data.use[, brand.ids])")  

  # Calculate means, and trim data frame for ggplot
  means.points <- candisc.obj$means[ ,c(xdim, ydim)]
  if (!isTRUE(all.equal(rotate, 0))) {
    points.rot <- cpm.rotate(means.points[ ,1:2], rotate)
    means.points[ ,1] <- points.rot[ ,1]
    means.points[ ,2] <- points.rot[ ,2]
  }

  names(means.points) <- c("xDim","yDim")

  # Calculate discriminant function SEs if needed
  if (plot.CI) {
    # need a temporary extraction, b/c for some reason ...
    CI.scores.tmp <- candisc.obj$scores                                        
    # ... it won't directly index from above :(
    CI.scores     <- CI.scores.tmp[ ,c(1, xdim+1, ydim+1)]
    # rotate the points if needed
    if (!isTRUE(all.equal(rotate, 0))) {
      CI.scores.rot <- cpm.rotate(CI.scores[ ,2:3], rotate)
      CI.scores[ ,2] <- CI.scores.rot[ ,1]
      CI.scores[ ,3] <- CI.scores.rot[ ,2]
    }
    # find confidence intervals
    CI.points1 <- ci.width * tapply( CI.scores[ ,2], CI.scores[ ,1], cpm.se) 
    CI.points2 <- ci.width * tapply( CI.scores[ ,3], CI.scores[ ,1], cpm.se) 
    CI.points <- cbind(CI.points1, CI.points2)

    CI.ends.upper <- means.points + CI.points
    CI.ends.lower <- means.points - CI.points
    CI.ends <- cbind(means.points, CI.ends.upper, CI.ends.lower)
    names(CI.ends) <- c("xDim", "yDim", "xDim.up", "yDim.up", "xDim.low", 
                        "yDim.low")
  }

  # Calculate attribute points, and trim data frame for ggplot
  if (coeffs == "std") {
    attribute.points.1 <- as.data.frame(candisc.obj$coeffs.std)
    if (!isTRUE(all.equal(rotate, 0))) {
      points.rot <- cpm.rotate(attribute.points.1[,1:2], rotate)
      attribute.points.1[,1] <- points.rot[,1]
      attribute.points.1[,2] <- points.rot[,2]
    }
    attribute.points.1 <- zoom.out*attribute.points.1

  } else {
    ## Raw score functionality is deprecated in v0.2
    ## 'raw' coeffs only make sense if raw means are also calculated,
    ##   - candisc function only reports standardized means
    # } else if(coeffs == "raw") {
    #  attribute.points.1 <- as.data.frame(zoom.out*candisc.obj$coeffs.raw)

    ### ==> placeholder for raw or other coefficient handling in the future
    warning(paste("Error: undefined coeffs parameter specified.",
                  "Only 'std' is supported at this time."))

    # for now just do the same thing as "std" coeffs
    attribute.points.1 <- as.data.frame(candisc.obj$coeffs.std)
    if (!isTRUE(all.equal(rotate, 0))) {
      points.rot <- cpm.rotate(attribute.points.1[,1:2], rotate)
      attribute.points.1[,1] <- points.rot[,1]
      attribute.points.1[,2] <- points.rot[,2]
    }
    attribute.points.1 <- zoom.out * attribute.points.1
  }
  attribute.points.init <- attribute.points.1[ , c(xdim, ydim) ]
  names(attribute.points.init) <- c("xDim", "yDim")
  x.start <- rep(0, nrow(attribute.points.init))
  y.start <- rep(0, nrow(attribute.points.init))
  attribute.points <- cbind(attribute.points.init, x.start, y.start)

  # Find max and min points for graph limits
  x.min.init <- min(0, min(means.points$xDim), min(attribute.points$xDim))
  x.max.init <- max(0, max(means.points$xDim), max(attribute.points$xDim))
  y.min.init <- min(0, min(means.points$yDim), min(attribute.points$yDim))
  y.max.init <- max(0, max(means.points$yDim), max(attribute.points$yDim))
  # Add 10% pad to X and Y dimentions for nicer plotting
  x.padding <- 0.1 * (x.max.init - x.min.init)
  y.padding <- 0.1 * (y.max.init - y.min.init)
  x.min <- x.min.init - x.padding
  x.max <- x.max.init + x.padding
  y.min <- y.min.init - y.padding
  y.max <- y.max.init + y.padding

  # Add text vector to data frame for ggplot
  point.text    <- row.names(means.points)
  means.points  <- cbind(means.points, point.text)
  means.points.b <- means.points

  means.points.b[ ,1] <- means.points[ ,1] + offset + label.jitter * rnorm(nrow(means.points), mean=offset, sd=abs(offset))
  means.points.b[ ,2] <- means.points[ ,2] + offset + label.jitter * rnorm(nrow(means.points), mean=offset, sd=abs(offset))

  # Trim attributes if needed, and add text vector to data frame for ggplot
  att.distance          <- sqrt(attribute.points$xDim^2 + 
                                  attribute.points$yDim^2)
  attribute.plot.points <- as.data.frame(
    attribute.points[att.distance >= quantile(att.distance, (trim)), ] )
  att.distance.alpha    <- 0.25 + att.distance * (0.75 / (max(att.distance)))
  arrow.text            <- row.names(attribute.plot.points)
  att.distance.alpha    <- att.distance.alpha[att.distance >= 
                                                quantile(att.distance, (trim))]
  attribute.plot.points <- cbind(attribute.plot.points, arrow.text, 
                                 att.distance.alpha)

  # rescale axes if needed
  if (aspect.lock) {
    x.min <- min(x.min, y.min)
    y.min <- x.min
    x.max <- max(x.max, y.max)
    y.max <- x.max
  }

  # build the ggplot2 plot, layer at a time
  #   1. basic structure plus dimensions
  #   2. individual scatter plot of responses, if desired ("plot.scatter")
  #   3. brand centroids, if desired ("plot.brands")
  #   4. brand confidence intervals, if desired ("plot.CI")
  #
  # basic plot with dimensions and nothing else
  cpm.p <- ggplot() +
    # label titles and axes
    labs(colour = title.legend) +
    labs(title = title.main) +
    theme(legend.text = element_text(size=12)) +
    theme(plot.title = element_text(size=20, lineheight=1, face="bold")) +
    theme(axis.text.x = element_blank(), axis.title.x=element_blank())  +
    theme(axis.text.y = element_blank(), axis.title.y=element_blank())  +
    # draw the dimensional arrows from origin
    geom_segment(data = attribute.plot.points, 
                 aes(x=x.start, y=y.start, xend=xDim, yend=yDim),  # cut: alpha
                 lwd=1, arrow=arrow(length=unit(0.3,"cm"), angle=30)) + 
    # label the dimensional arrows
    geom_text(data = attribute.plot.points, 
              aes(x=xDim, y=yDim, label=arrow.text),  # cut: alpha
              hjust=0.5, vjust=1.5, size = I(6)) +
    # set the chart boundaries
    coord_cartesian(xlim = c(x.min, x.max), ylim = c(y.min, y.max)) + 
    # nice background
    theme(panel.background = element_rect(colour="white", fill="grey95"))

  if (plot.scatter) {
    # find individual scores
    ind.points <- candisc.obj$scores[ ,c(1, xdim+1, ydim+1)]
    if (!isTRUE(all.equal(rotate, 0))) {
      points.rot <- cpm.rotate(ind.points[ ,2:3], rotate)
      ind.points[ ,2] <- points.rot[ ,1]
      ind.points[ ,3] <- points.rot[ ,2]
    }

    names(ind.points) <- c("this.group", "xDim", "yDim");
    # scatter plot of individual responses
    cpm.p <- cpm.p + 
      geom_point(data = ind.points, 
                 aes(x=xDim, y=yDim, colour=factor(this.group)), 
                 size=4, alpha=0.5)
  }
  if (plot.brands) {
    # label the centroids (brands)
    cpm.p <- cpm.p +
      geom_point(data=means.points, aes(x=xDim, y=yDim), pch=22,    # points
                 colour=I("blue"), fill=I("blue"), size=4) +
      geom_text(data=means.points.b,                                                                   # labels
                aes(x=xDim, y=yDim, label=point.text),
                hjust=0.5, vjust=1.5, size = I(6*font.mult), colour="darkred")
  }
  if (plot.CI) {
    cpm.p <- cpm.p +
      geom_segment(data=CI.ends, 
                   aes(x=xDim, y=yDim.low, xend=xDim, yend=yDim.up), # vertical arrows
                   lty=3, lwd=2, colour=I("blue")) +
      geom_segment(data=CI.ends, 
                   aes(x=xDim.low, y=yDim, xend=xDim.up, yend=yDim), # horiz arrows
                   lty=3, lwd=2, colour=I("blue")) +
      geom_rect(data=CI.ends, 
                mapping=aes(xmin=xDim.low, xmax=xDim.up, 
                            ymin=yDim.low, ymax=yDim.up),   # shaded boxes 
                fill=I("lightblue"), color="black", alpha=0.2)
  }

  return(cpm.p)
} # end cpm.plot()

Code Block 2: Analysis code

These are all of the analysis commands used in this post.

You'll need the following packages: plyr, dplyr, tidytext, ggplot2, corrplot, textdata, GPArotation, candisc . You could install those packages, if needed, with this command: install.packages(c("plyr", "dplyr", "tidytext", "ggplot2", "corrplot", "textdata", "GPArotation", "candisc"))

Note if you have a Mac: depending on your system details, you also might need the XQuartz system (for package dependency reasons that are somewhat unclear). If you get a bunch of "rgl" errors, you'll know that you need it.

## https://quantuxblog.com/multidimensional-sentiment-analysis-part-2
## all the code for Sentiment Analysis part 2
## ... except for the separate CPM functions in code block 1

## Load coded sentiment data, from blog part 1:
## https://quantuxblog.com/multidimensional-sentiment-analysis-part-1
shake.sent <- readRDS(url("https://quantuxbook.com/misc/shakespeare-sentiment.Rds"))
head(shake.sent)

## correlations among sentiments
library(corrplot)
corrplot.mixed(cor(shake.sent[ , c(-11, -12)]),  # -11 to remove name of the work, -12 to remove sum
               upper="ellipse", 
               upper.col=colorRampPalette(c("red","lightgoldenrod","darkblue"))(200),
               lower.col=colorRampPalette(c("red","lightgoldenrod","darkblue"))(200),
               tl.cex=1, tl.pos="lt", diag="u",
               number.cex=0.8, 
               order="hclust")

## exploratory factor analysis (example)
library(GPArotation)  # install if needed
# try a 4 factor solution
factanal(shake.sent[ , c(-11, -12)], factors=4, rotation = "oblimin")


## PERCEPTUAL MAP of the works vs sentiment dimensions
## Be sure to source the CPM functions in Code Block 1 above, or will get errors

# on some systems, e.g., Macbook with M2 and OS Sonoma, 
# this requires installation of XQuartz for somewhat opaque reasons
# ==> https://www.xquartz.org

# set up the data
sent.ratings <- shake.sent[ , 1:11]   # just ratings + platform
# keep only the rows where there is some sentiment
sent.ratings <- sent.ratings[rowSums(sent.ratings[ , 1:10]) > 0, ]
head(sent.ratings)

# overall totals
aggregate(. ~ Work, data=sent.ratings, mean)

# plot dimensions only, and excluding the Sonnets
p <- cpm.plot(subset(sent.ratings, Work  != "Sonnets"), 
              "Work", names(sent.ratings[1:10]),
              plot.scatter=FALSE, plot.CI=FALSE,
              offset=0.05, 
              plot.brands = TRUE, aspect.lock = TRUE,
              zoom.out = 0.3, rotate = 20, 
              title.main = "Perceptual Map, Five Shakespeare Works")
p

Multidimensional Sentiment Analysis (Part 2)