Normal Distribution: A Statistical Symphony in Data Science
 Saurabh Naik
Saurabh NaikTable of contents
- Introduction:
- Normal Distribution:
- Parameters of Normal Distribution:
- Importance of Normal Distribution:
- PDF Equation for Normal Distribution:
- Standard Normal Distribution:
- PDF Equation for Standard Normal Distribution:
- Advantages of Transforming to Standard Normal Distribution:
- Ways to Transform to Standard Normal Distribution (Z-score):
- Properties of Normal Distribution:
- Use of Normal Distribution in Data Science:
- Conclusion:
Introduction:
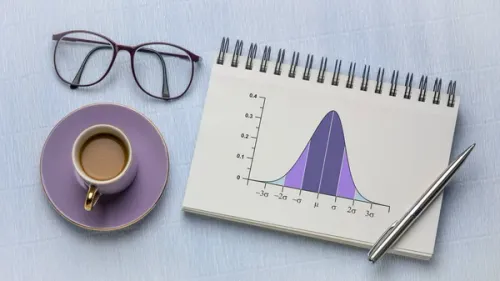
Normal distribution, also known as Gaussian distribution, plays a pivotal role in the realm of statistics and data science. Its symmetrical bell curve has far-reaching implications, shaping our understanding of randomness, variability, and real-world phenomena.
Normal Distribution:
Normal distribution is a continuous probability distribution that forms a bell-shaped curve when plotted. It is characterized by a symmetric, mound-shaped density function.
Parameters of Normal Distribution:
The two key parameters are the mean (μ), representing the center of the distribution, and the standard deviation (σ), indicating the spread or dispersion of the data.
Importance of Normal Distribution:
A normal distribution is omnipresent. A classic example is human height, where the majority of people cluster around the average height, forming a bell curve.
PDF Equation for Normal Distribution:
The Probability Density Function (PDF) for normal distribution is given by: \(f(x|\mu, \sigma) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \)
\(\mu \) : Mean(It controls the position of curve on X axis)
\(\sigma\): Standard Deviation (It controls the spread on the X-axis)
Standard Normal Distribution:
A special case where the mean \(\mu\) is 0 and the standard deviation \(\sigma\) is 1, simplifying computations and comparisons across different normal distributions.
PDF Equation for Standard Normal Distribution:
\(\phi(z) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}z^2} \)
- ( z ): Z-score (number of standard deviations from the mean)
Advantages of Transforming to Standard Normal Distribution:
Facilitates comparison between different normal distributions, aids in statistical hypothesis testing, and simplifies data interpretation.
Ways to Transform to Standard Normal Distribution (Z-score):
\(z = \frac{x - \mu}{\sigma}\) This transformation involves subtracting the mean and dividing by the standard deviation, providing a normalized scale.
Properties of Normal Distribution:
a. Symmetry: The curve is symmetric around the mean.
b. Central Tendencies: Mean, median, and mode coincide.
c. No Skewness: The distribution is free from skewness.
d. Area Under Curve is 1: The total probability under the curve is always 1.
e. Empirical rule: 68% of data is present in 1st standard deviation. 97% data is present in 2nd standard deviation and 99% data is present in the third standard deviation.
Use of Normal Distribution in Data Science:
Model Assumptions: Many statistical techniques assume normality.
Statistical Inference: Hypothesis testing and confidence intervals rely on a normal distribution.
Predictive Modeling: Gaussian assumption aids various machine learning algorithms.
Conclusion:
In the vast landscape of data science, understanding and harnessing the power of normal distribution illuminates our journey through statistical analysis and model building. As we traverse the symmetrical contours of this statistical symphony, we unlock the doors to insightful interpretations and robust predictions.
Subscribe to my newsletter
Read articles from Saurabh Naik directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Saurabh Naik
Saurabh Naik
🚀 Passionate Data Enthusiast and Problem Solver 🤖 🎓 Education: Bachelor's in Engineering (Information Technology), Vidyalankar Institute of Technology, Mumbai (2021) 👨💻 Professional Experience: Over 2 years in startups and MNCs, honing skills in Data Science, Data Engineering, and problem-solving. Worked with cutting-edge technologies and libraries: Keras, PyTorch, sci-kit learn, DVC, MLflow, OpenAI, Hugging Face, Tensorflow. Proficient in SQL and NoSQL databases: MySQL, Postgres, Cassandra. 📈 Skills Highlights: Data Science: Statistics, Machine Learning, Deep Learning, NLP, Generative AI, Data Analysis, MLOps. Tools & Technologies: Python (modular coding), Git & GitHub, Data Pipelining & Analysis, AWS (Lambda, SQS, Sagemaker, CodePipeline, EC2, ECR, API Gateway), Apache Airflow. Flask, Django and streamlit web frameworks for python. Soft Skills: Critical Thinking, Analytical Problem-solving, Communication, English Proficiency. 💡 Initiatives: Passionate about community engagement; sharing knowledge through accessible technical blogs and linkedin posts. Completed Data Scientist internships at WebEmps and iNeuron Intelligence Pvt Ltd and Ungray Pvt Ltd. successfully. 🌏 Next Chapter: Pursuing a career in Data Science, with a keen interest in broadening horizons through international opportunities. Currently relocating to Australia, eligible for relevant work visas & residence, working with a licensed immigration adviser and actively exploring new opportunities & interviews. 🔗 Let's Connect! Open to collaborations, discussions, and the exciting challenges that data-driven opportunities bring. Reach out for a conversation on Data Science, technology, or potential collaborations! Email: naiksaurabhd@gmail.com