Tuples

Tuples are in-built data structures in Python that are similar to lists, except that tuples are immutable (i.e., contents cannot be changed).

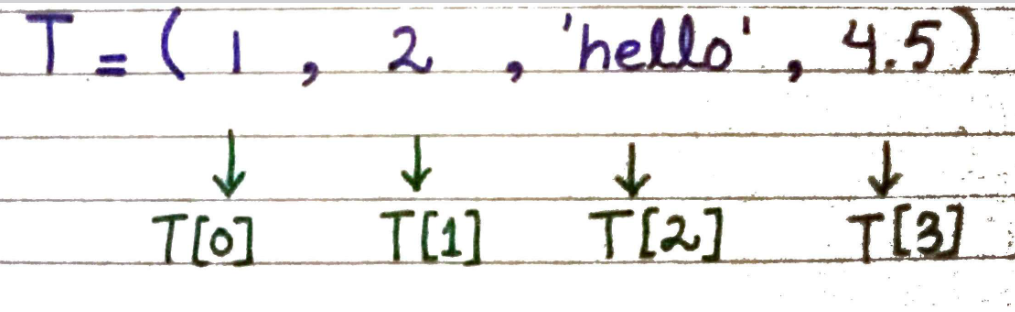
Creating a Tuple

# empty tuple
t = ()

# tuple with single item
t = ('hello',)

# Homogeneous tuple
t = (1, 2, 3, 4)

# Heterogenous tuple
t = (1, 2, 3.5, [4, 5], 'hello') 

# 2D tuple
t = (1, 2, 3, 4, (5, 6))

# Using type conversion
t = tuple('hello')   # ('h','e','l','l','o')

Accessing Items in tuples

t = (1, 2 , 3, 4) 

# indexing
print (t[2]) # 3 is extracted
print (t[-2]) # 3 is extracted

# slicing
print(t[0:4]) # (1, 2, 3)
print([0:4:2]) # (1 , 4) 
print ([-3:-1]) # (2, 3)

# reversing a tuple
print(t[:,:,-1])

# Accessing items in 2D list
t = (1, 2, 3, 4, (5, 6))
print(t[4][0]) # 5 is extracted

Deleting a tuple

Deleting the parts of the tuple is not possible, as tuples are immutable.

t = (1, 2, 3)
del t

Operation on Tuple

# Arithmetic (+ and *)
t = (1, 2, 3)
t1 = (4, 5 , 6)

print(t+t1) # Output: (1, 2, 3, 4, 5 ,6)

print(t*2) # Output: (1, 2, 3, 1, 2, 3)

# Membership Operators
t = (1, 2, 3)
1 not in t  # Output: False
2 in t      # Output: True

# Iteration (loops)
t = ('bag', 'shoes', 'clothes')
for i in t:
    print(i)


# while loop
while i  < len(t):
    print(t[i])
    i+=1

# Output:
# bag
# shoes
# clothes

Tuple functions & methods

t = (1, 2, 3, 4)

# Functions
len(t) # Output: 4
sum(t) # Output: 10
min(t) # Output: 1
max(t) # Output: 4
sorted(r, reverse= True) # Output: [4, 3, 2, 1]

# Tuple Methods

# count the number of times element appears
t.count(1) # Output: 1

# returns the index position of an element
t.index(3) # Output: 2

Tuple unpacking

Extracting values from the tuple to variables.

a, b, c = (2, 4 ,6)

print(a) # Output:  2
print(b) # Output:  4
print(c) # Output:  6

a, b, *others = (1, 2, 4, 5, 6)
print(a, b) # Output: 1 2 
print(others) # [4, 5 ,6 ]

Zipping Tuples

a = (1, 2, 4)
b = (5, 6 , 7)
zip(a,b) # returns the zip object

# To view the zip object , we need to convert to list or tuple
tuple(zip(a,b))

# Output: 
# ((1, 5), (2, 6), (4, 7))

---

Sets

A set is an unordered collection of data . Each element in a set is unique (no duplicates) and must be immutable.

Note: Set itself is mutable, we can add or remove items from it. However, set does not contain mutable data types. That's why multi-dimensional sets are not possible.

Creating a Set

# Empty set
s = set()

# Homogenous set
s = { 4, 5, 6}

# Heterogenous set
s = {True, 1.8, (1,2,4),'hello'}

# As sets are un-ordered so s1 == s2,
s1 = {1,2,3}
s2 = {2,1,3}
print(s1 == s2) # Output: True

Accessing & Editing Items in Sets

Sets are unindexed. They do not follow the concept of accessing items through indexing and slicing. Editing items is also not possible in sets.

Adding items in Sets

s = {1, 7, 3, 4}

# add (add single item in set)
s.add(5)
print(s) # Output: {1, 3, 4, 5, 7}


# update (add multiple items in set)
s.update([9, 0, 19])
print(s) # Output: {0, 1, 3, 4, 5, 7, 9, 19}

Deleting Items from Sets

We cannot delete particular items from sets. So, either we need to delete using the element or delete the entire set.

s = {1, 2, 3, 4}
del s

s = {1, 3, 4, 5}
s.discard(5)
print(s)

# Output: {1, 3, 4}

#  Unlike discard, remove function will throw an error when that element does not exsist
s = {1, 3, 4, 5}
s.remove(5)
print(s)

# Output: {1, 3, 4}

# Randomly remove any element from the set
s = {1, 3, 5, 6 }
s.pop()
print(s)

# Output: {3, 5, 6}

# Empties the set
s = {1, 3, 7, 2}
s.clear()
print(s)

# Output: set()

Set Operations

s1 = {1,2,4,5}
s2 = {4,5,6,7,2}

# Union
s1 | s2        # {1, 2, 4, 5, 6, 7}

# Intersection
s1 & s2        # {2, 4, 5}

# Difference
s1 - s2        # {1}
s2 - s1        # {6, 7}

# Symmetric Difference(^) --> All items except common ones

s1 ^ s2        # {1,6,7}

# Membership operators
1 in s1        # True
4 not in s2    # False

# iteration (loops)
for i in s1:
    print(i, end = " ")   # 1 2 4 5

Set Functions & Methods

# Functions
s = {3, 4, 5, 1}

len(s)        # 4
sum(s)        # 13
max(s)        # 5
min(s)        # 1
sorted(s)     # [1, 3, 4, 5]


# Methods
s1 = {1, 3, 2}
s2 = {4, 7 ,8}

# Union 
s1.union(s2)           # {1, 2, 3, 4, 7, 8}

# intersection
s1.intersection(s2)    # set()

# Difference 
s1.difference(s2)      # {1, 2, 3}

# Symmetric difference
s1.symmetric_difference(s2)   # {1, 2, 3, 4, 7, 8}

# isdisjoint() --> are s1 and s2 are disjoints(no element is common)
s1.disjoint(s2)        # True

# issubset() --> Is s1 is subset  of s2?
s1.issubset(s2)        # False

#issuperset()--> Is s1 is superset of s2?
s1.issuperset(s2)    # False

# copy --> creates a shallow copy 
s3 = s1.copy()
print(s3)            # {1, 2, 3}

Frozenset

Frozenset is similar to sets except it is immutable (no item can be added or removed)

Syntax: frozenset(iterable) --> iterable can be a tuple, list or dictionary.

# Creating Frozenset
f1 = frozenset([1,2,3])

Frozenset Operations

A = frozenset([1,2,3])
B = frozenset([4,5,6])

# Union
print(A.union(B))               # Output: frozenset({1, 2, 3, 4, 5, 6})

# Intersection
print(A.intersection(B))        # Output: frozenset()

# Difference
print(A.difference(B))           # Output: frozenset({1, 2, 3})

# Symmetric_difference
print(A.symmetric_difference(B)) # Output: frozenset({1, 2, 3, 4, 5, 6})

Set Comprehension

Syntax : new_Set = {expression for element in iterable}

new_Set = {expression for element in iterable if condition}

# Create a set of elements containing squares from 1 to 5
{i*i for i in range(1,6)}

# Output: {1, 4, 9, 16, 25}

# Create a set of elements containg even numbers from 1 to 10
{i for i in range(1,11) if i % 2 == 0}

# Output: {2, 4, 6, 8, 10}