This article is a summary of Chapter 2 of:

Yazawa, H. (2015). 程序是怎么跑起来的[How Program Works] (L. Fengjun, Trans.). People's Posts and Telecommunications Press

Reason for using Binary in Computers

Computers are constructed by integrated circuits (IC). The pins on each IC has ony two states: 0V or 5V. Since there are only two states, the pin can only represent a binary number, where 0V indicates a 0 and 5V indicates a 1. Each binary digit is called a bit.

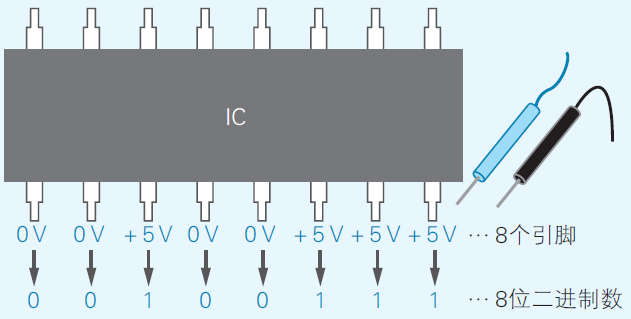
(Yazama, 2015 Fig. 2-1)

Every 8 bits is called a byte. A bit is the minimum unit, and a byte is the basic unit of information. In other words, computers always read and store data in bytes instead of single bits. If a number has fewer digits than a byte, its upper digits are filled with zeros. For example, 100111 will be stored as 00100111 in computers.

Conversion between Binary and Decimal

For any number, a digit at a given place represents the value of the digit times the power of position of the base. In decimal system where the base is 10, 39 would mean 3 X 10^1 + 9 X 10^0. The only difference for binary system is that the base is 2 instead of 10. For example, 00100111 would be 1 X 2^5 + 1 X 2^2 + 1 X 2^1 + 1 X 2^0

(Yazama, 2015, Fig 2-3)

Shifting Operation in Binary

Shifting operation means "moving" each digit to a different place. It includes shifting left (moving each digit to higher places), and shifting right (moving each digit to lower places). The empty lower places after left shifting will be filled with 0 (we will talk about empty places for right shifting later), and the overflow digits are discarded. For example:

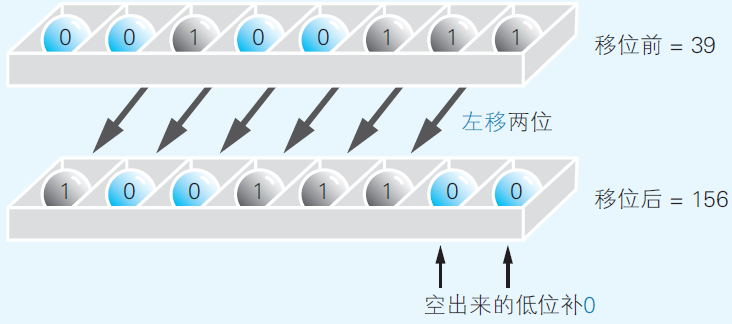
(Yazama, 2015, Fig 2-4)

Fig 2-4 represents shifting number 00100111 (binary for 39) to the left by 2 places. The two zeros at the top two places are discarded, and the two empty places at the two lowest places after the shifting are filled with zeros. The resulting binary number is 10011100 (156), which turns out to be 4 times 39. Shifting operation can replace multiplication operation to some extent. For binary numbers, shifting left by N places would multiply the number by 2^N (shifting right would multiple by 2^-N). Similarly, for decimals shifting left by N places would multiply the number by 10^N

Complement Number

Before we talk about right shifting in detail, we need to first understand the concept of complement number. Normally, when representing both positive and negative integers in binary numbers, the highest place is used to indicate sign, in which 0 represents a positive number and 1 represents negative a number. However, converting a number to its opposite number involves more than switching the highest place. The reason for that is by definition of opposite numbers, their sum must be zero. For example, 1 + (-1) = 0, but 00000001 + 10000001 = 10000010, not zero.

The correct way is to calculate the complement number. Using the Two's Complement method, the complement number is calculated by fliping the digit at each place (changing 1 to 0 and 0 to 1), and adding the result by 1. For example, for 1 + (-1):

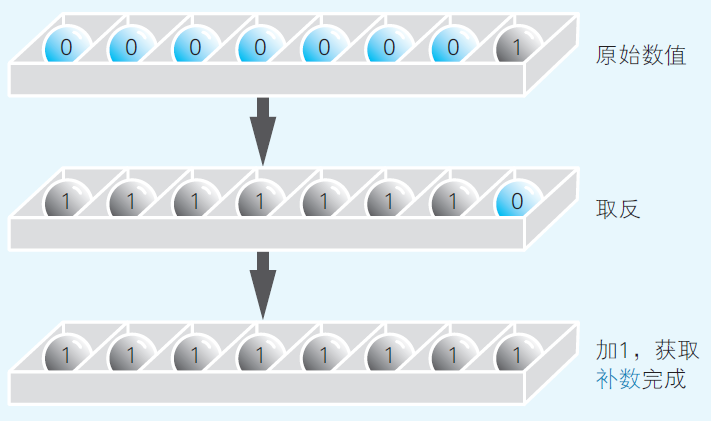
(Yazama, 2015, Fig 2-5)

The complement number for 00000001 is 11111111. The sum will be 100000000, and since the byte only has 8 places, the leading 1 will be omitted, and the results turns to be 00000000, which is zero. Remember that computers always do subtraction through addition.

Whether the highest place is used to indicate sign or is another number place depends on the integer data type. For example, in C, unsigned int makes the highest place a number place, meaning that it cannot represent negative integers (so it is "unsigned"), while int makes the highest place a sign indicator. Furthermore, since the value zero is 00000000, starting with a leading 0, zero is usually considered as a positive number in this definition.

Logical Right Shifting and Arithmetic Right Shifting

There are two types of right shifting, logical right shifting and arithmetic right shifting. (In fact, there are also logical left shifting and arithmetic left shifting, but they have the same way of calculation, appending zeros on the left)

Logical right shifting is used if we consider the number only as a sequence of 0 and 1, instead of a complete binary number. For example, on an LED screen 0 represents an unlit pixel and 1 represents a light one. In logical right shifting, the empty places are filled with 0.

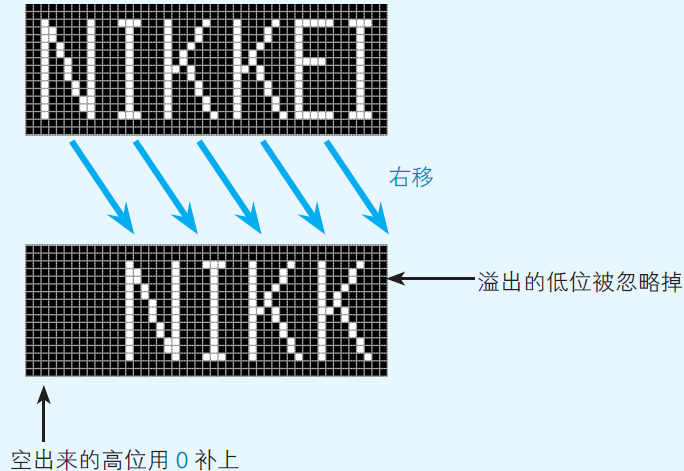
(Yazama, 2015, Fig 2-9)

In arithmetic right shifting, the empty places are filled with the sign place of the number, that is, 0s are added for positive numbers and 1s are added for negative numbers.

For example, 11111100 (-4) after logical right shifting will be 00111111 (63), and after arithmetic right shifting will be 11111111 (-1), as shown in Fig 2.10

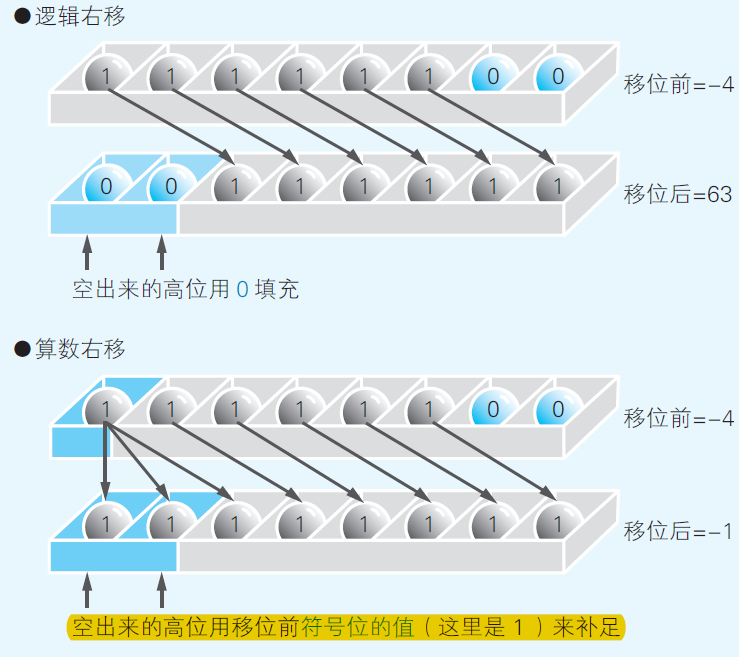
(Yazama, 2015, Fig 2-10)

Sign extension is the operation that converts a number to a larger data type, such as converting a byte (8 places) to a short (16 places) or int (32 places), while keeping the value the same. Similar to arithmetic right shifting, sign extension is also achieved through filling the additional places with the sign place, that is, 0 for positive numbers and 1 for negative numbers, as shown in Fig 2-11

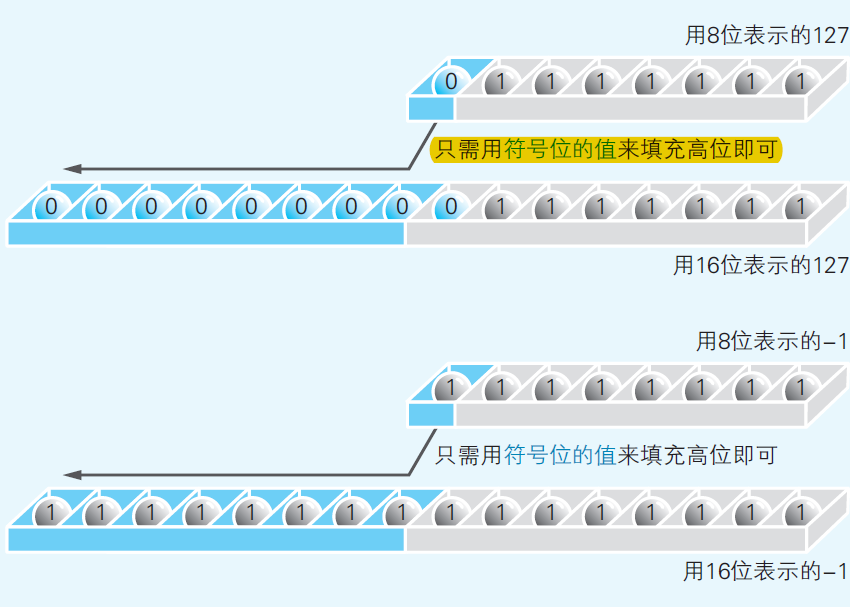
(Yamaza, 2015, Fig 2-11)

Logical Calculation

As we previously mentioned, logical calculation treats every digit as a single 0 or 1. In other words, there are only two numbers 0 and 1.

Logical calculations include:

1 NOT: convert 0 to 1 and 1 to 0

2 AND: returns 1 when both inputs are 1, 0 otherwise

3 OR: returns 0 when both inputs are 0, 1 otherwise

4 XOR (sometimes also called EOR, meaning exclusive or): returns 1 when exactly one input is 1 and the other is 0, 0 otherwise.

For example, in an LED screen if we consider a bright pixel as 1 and a dark pixel as 0, the logical calculations performed on the screen will be like Fig 2-12

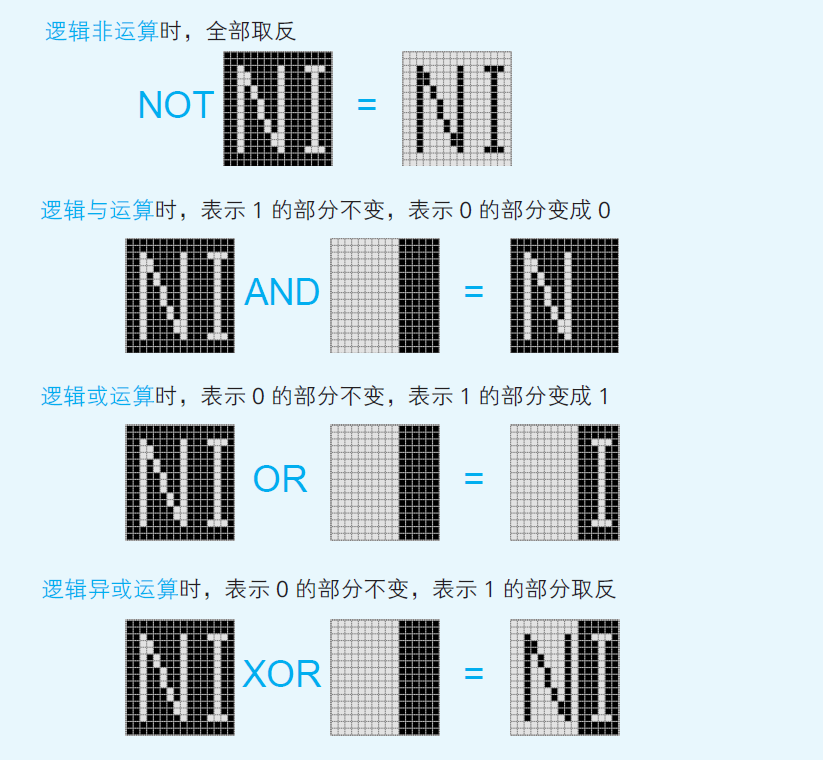
(Yazama, 2015, Fig 2-12)

Learning Notes: Data is Represented in Binary