Demystifying Searching Algorithms: Unveiling the Intricacies of Linear and Binary Search

This technical documentation covers the following topics:

Introduction:

• Overview of searching algorithms, with a focus on linear and binary search.

What is Searching?

• Definition: Finding the index of an element in an array.

Linear Search:

• Definition and example.

• Time complexities in the best, average, and worst cases.

• When to use linear search (unsorted lists).

Binary Search:

• Analogy with a sorted contact list.

• Technical definition.

• Three key points in the algorithm.

Binary Search Process:

• Initialization and the role of low, middle, and high pointers.

• Step-by-step comparison process.

• Conclusion of a successful or unsuccessful search.

Time Complexities:

• Time complexities of linear search in the best, average, and worst cases.

• Time complexities of binary search in the best, average, and worst cases.

Conclusion:

• Summary of key points.

• Appreciation for reading, and an invitation for feedback.

Introduction: In this technical documentation, we will delve into the world of 'Searching Algorithms'.

• What is searching?

• What are the different types of searching (Linear and Binary Search) and their time complexities?

1) What is searching:

Searching, as the name implies, is the process of "finding the index number of a specific element within an array."

Let's illustrate this with an example: Consider an array [1, 5, 9, 11, 13, 17]. In this array, we aim to determine the index of the target element, which, in this case, is 11. There exist two fundamental algorithms for achieving this:

a) Linear Search Algorithm.

b) Binary Search Algorithm.

We will explore why and when we use these algorithms.

a) Linear Search*:* Imagine you have a list of contacts in your phone. Linear search is like checking each contact in order until you find the one you're looking for.

Let's say you're looking for a specific contact, like a friend's name. You start from the beginning of your contacts and look at each name one by one. If you find the friend's name, you stop and say where you found it. If you go through the whole list and don't find the name, you say it's not there.

In simpler terms, it's like looking for a friend's contact in your phone. You check each name until you find it. If you find it, great! If not, you say you couldn't find it. Linear search works the same way but with names in your contact list. If it finds the name, it tells you where it is. If not, it says it couldn't find it and gives you -1 as a sign that it didn't find the contact you were looking for.

• Technical Definition of Linear Search: Linear search is one of the most straightforward and simple searching algorithms. It is employed to search for an element or its index in an array or ArrayList. This algorithm operates in a sequential manner, scanning through the entire array. It meticulously compares each element in the array with the target element.

  If it finds the target element, it promptly returns the index of the element or your desired output. If the target element remains elusive, it methodically proceeds to the next element. In the event that the target element is not discovered, the program gracefully returns -1 as the output. A visual representation of this process is shown below.

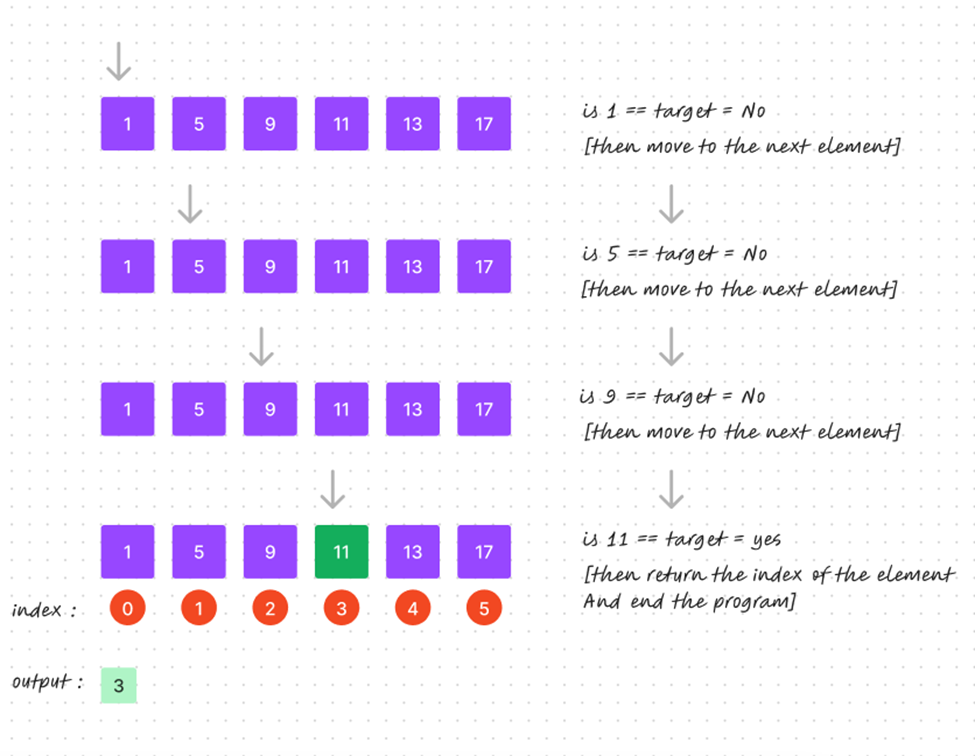
Time complexity of Linear Search:

The time complexity of the linear search algorithm depends on the position of the element in the array or list, leading to three distinct cases:

I) Best Case

II) Average Case

III) Worst Case

• Best Case: In the best-case scenario, the target element is located at the 0th index, indicating that we've found the element right at the beginning of the list. In this situation, there's no need for further comparisons, resulting in a time complexity of O(1). Here, "1" represents the number of comparisons made.

• Average Case: In the average case, the expected time complexity is also O(n). This assumes that there is no specific pattern or order in the data, and the target element is equally likely to be found anywhere in the list. On average, you would need to check about half of the list before finding the target element.

• Worst Case: In the worst-case scenario, the element we are trying to find is either at the last index of the list or not present in the list at all. In this case, the time complexity of the algorithm will be O(n), where "n" represents the number of comparisons made in the program.

When should we use Linear Search? As we can see from the above explanation, linear search is very beginner-friendly and simple to use, making it easy for beginners. It is most useful when the list is unsorted. (An array or list is considered unsorted when all the elements are not arranged in a specific order).

So this is all about linear search but the linear search algorithm is beginner friendly but not the good performance wise. So instead of this we use ‘Binary Search algorithm’ for searching the element in the array.

B) Binary Search*:* Now imagine you have a sorted list of contacts in your phone (A list or array is considered sorted when its elements are arranged in a specific order, usually in ascending or descending order based on the values of the elements), alphabetically arranged. Binary search is like a more efficient way of finding a contact compared to linear search.

In binary search, you start by looking at the middle contact in your list. If the name matches the one you're searching for, great! You've found it. If the name comes before the middle contact alphabetically, you now focus on the first half of the list and repeat the process. If the name comes after the middle contact, you focus on the second half of the list and again repeat the process.

You keep narrowing down your search by half until you find the contact or determine that it's not in your list. The key here is that binary search exploits the sorted nature of the list, making the process more efficient than checking each contact one by one.

If binary search finds the contact, it tells you where it is in the list. If the contact isn't there, it signals this by, for example, returning -1 to indicate that the search was unsuccessful.

• Technical Definition of Binary Search: Binary search is the most commonly used, efficient, and versatile searching algorithm. Binary search is employed on arrays that are sorted. It follows the 'divide and conquer' rule, which means it divides the array or list into two halves by selecting a middle point and then compares the middle point with the target element.

In the binary search algorithm, there are three key points as follows:

1. Find the middle element.

2. If the target element is greater than the middle element, search in the right half; otherwise, search in the left half.

3. If the middle element is our target element, then its index is our answer.

Here's how Binary Search works using example array [1, 3, 7, 9, 13, 17, 21, 43, 51] target element - 17:

First, we initialize three pointers: 'low,' 'middle,' and 'high.'

• The 'low pointer' is used to track the lower bound or index of our search range in the array. Initially, it is usually set to the 0th index, but it will update to reflect the new and reduced search range of the array, changing accordingly with the middle element. If the target element is greater than the middle element, the array's search range is reduced by setting 'low = middle + 1' index.

• The 'high pointer' is used to track the upper bound or index of the array within our current search range. Initially, we set the high pointer to the last index of the array using the rule or formula: 'high = array’s length - 1'. We subtract -1 from the length because array indexing starts at 0. For example, if the array's length is 5, and we position the low pointer at the array's length, the index would be out of bounds. The high pointer is updated when the target element is greater than the middle element and when it needs to reflect the upper bound of our new and reduced array range using this formula: 'high = middle - 1'.

• The 'middle pointer' plays a crucial role in this searching algorithm because the comparisons are made using the middle pointer. We initialize the middle pointer or index with this formula: 'middle = (low + high) / 2'. The middle pointer doesn't need to be updated using an external formula; it updates automatically as the low and high pointers change.

First Comparison:

Compare the middle element (index 4, value 13) with the target element (17).

Since the target element is greater than the middle element, update 'low' to 'middle + 1,' narrowing the search range to the right half of the array.

Second Comparison:

Recalculate the middle index within the new search range (5 + 8) / 2 = 6.

Compare the middle element (index 6, value 21) with the target element (17).

Since the target element is less than the middle element, update 'high' to 'middle - 1,' narrowing the search range to the left sub-array.

Third Comparison:

Recalculate the middle index within the updated search range (5 + 5) / 2 = 5.

Compare the middle element (index 5, value 17) with the target element (17).

They are equal, indicating that the target element is found at index 5.

Conclusion:

The binary search algorithm successfully located the target element (17) at index 5 in the given array. In cases where the target element is not found, the algorithm returns the value -1. This ensures a clear indication when the search concludes without locating the desired element in the array. A visual representation of this process is shown below.

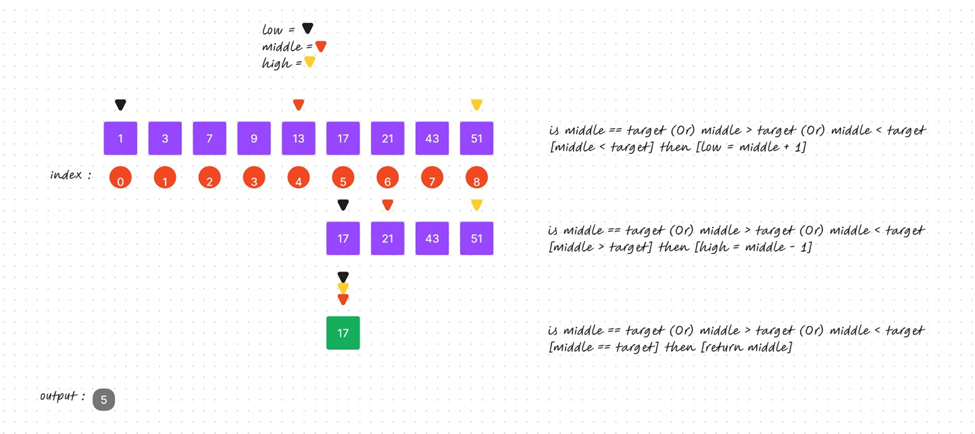
Time complexity of binary search: The time complexity of the any search algorithm depends on the position of the element in the array or list, leading to three distinct cases:

I) Best Case

II) Worst Case

III) Average Case

• Best case: In binary search, the best-case scenario occurs when we find our target element in the first comparison, meaning our middle element is our target element. In this case, the time complexity will be O(1), where 1 is the number of comparisons made.

• Worst Case: In binary search, the worst case is when our target element is located at the last possible position, or it is not even present in the array or list. In this case, the time complexity of the algorithm will be O(log n).

• Average Case: In binary search average case time complexity is O(log n).

This concludes our discussion on binary search and searching algorithms.

Note: Hey, everyone who reads this technical documentation, thank you for taking the time to read it. I am delighted to inform you that this is my first attempt at writing technical documentation. I would appreciate receiving your feedback, whether it is positive or suggestions for improvement.

Here is my X profile; you can connect with me there: https://x.com/Vvekstwt