Why Binary Search is better than Linear Search?

Welcome to my new blog, we discuss how Binary search is more efficient and speedy than Linear Search.

Linear Search in an array or a list goes through each item to find the target item.

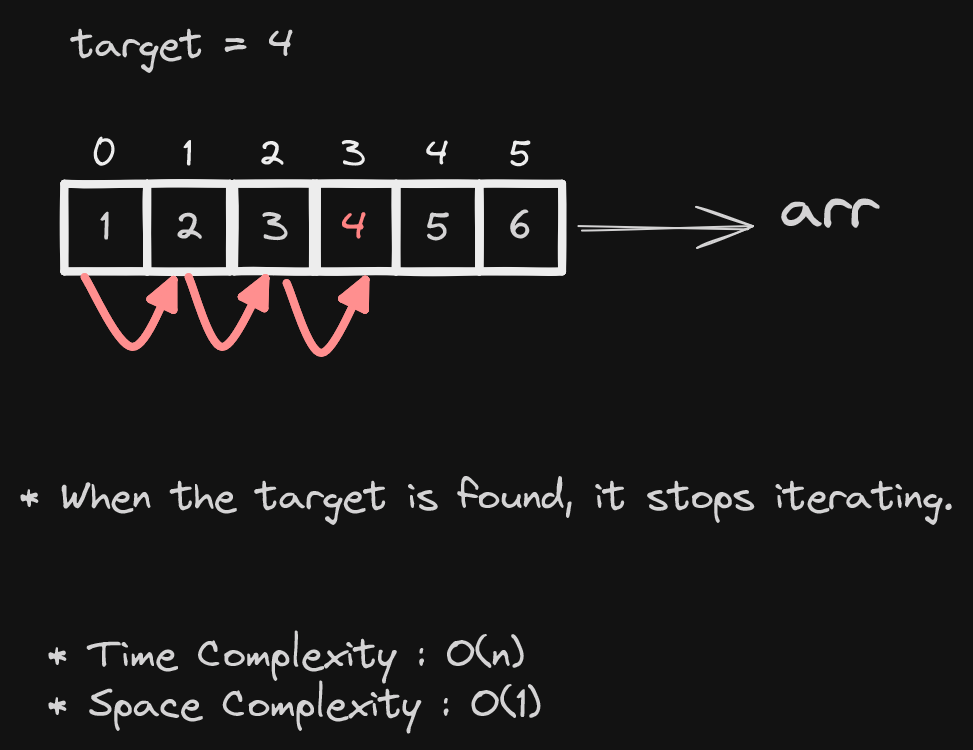
For example, let [1, 2, 3, 4, 5, 6] be an array and its length is six. Let the target item be 4. So in Linear Search, it will go through each item and when the desired item is found it'll return the value.

Here is how it happens.

Here is the code sample:

def linearSearch(arr, target):
    for i in target: 
        if target == i:
            return i
    return None

As it runs 'n' times for searching, the time complexity is O(N). Because

$$\displaylines{ T(N) = O(N) + O(1) \\ => T(N) = O(N)}$$

Here T represents the time taken to complete the task and as the task is done only in one array, the space complexity is O(1).

Hope all of you get this. Let's move to Binary Search. In Binary Search, we generally adopt the Divide and Conquer method.

1. Firstly, we search for the middle item of an array (n/2).

2. Then compare the middle item with the adjacent item of the array.

3. If the left adjacent is higher than the mid, then we have to look at the left half only. (if arr[n/2] < arr[n/2 - 1], consider arr[0] to arr[n/2-1])

4. If the above doesn't satisfy and if the right adjacent is higher than the mid, then we have to look at the right half only. (if arr[n/2] < arr[n/2 + 1], consider arr[n/2+1] to arr[n-1])

5. If both of the conditions are not true, then the middle item is the target item.

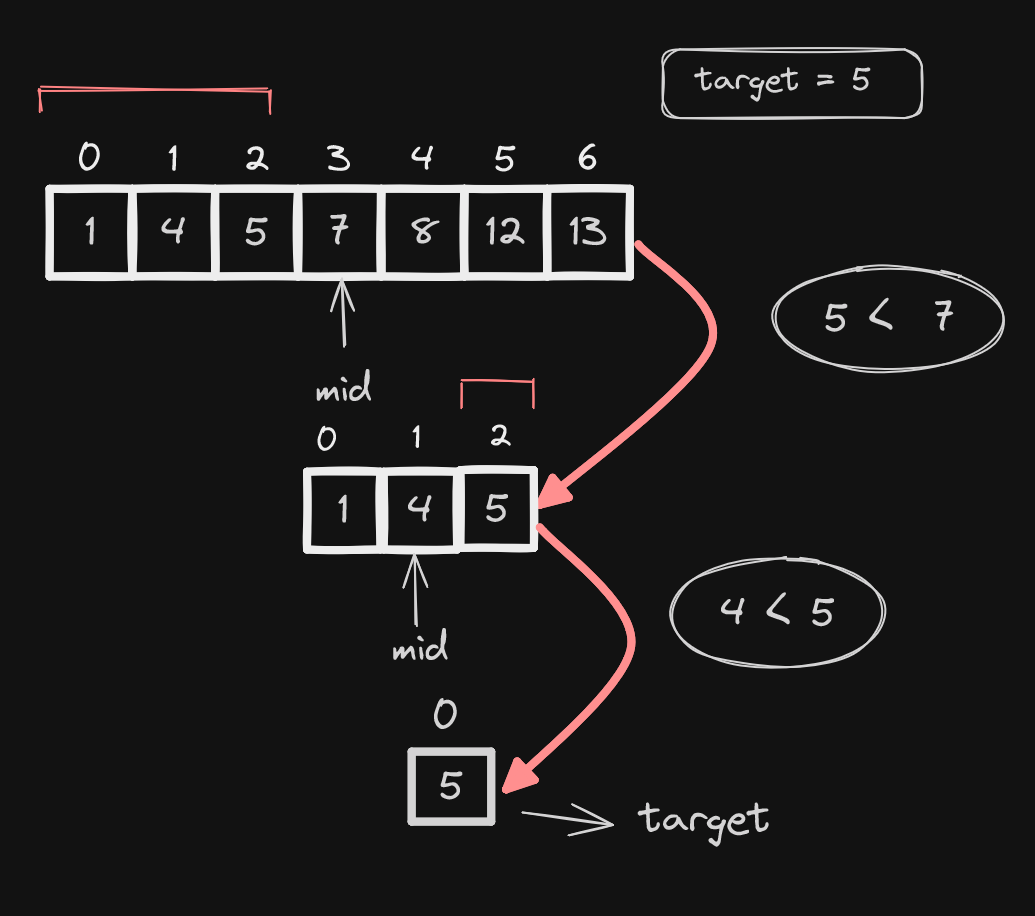
For better understanding let's have another example. Let an array be [1, 4, 5, 7, 8, 12, 13] and the target is 5.

Let's see how it works.

Following the above here is the code.

def binarySearch(arr, target):
    start = 0
    end = len(arr)-1
    while start <= end:
        mid = start + (end - start) // 2
        midValue = arr[mid]
        if midValue == target:
            return mid
        elif target < midValue:
             end = mid - 1
        else:
             start = mid + 1
    return None

As it runs 'n/2' times, the time complexity is as follows:

$$\displaylines{T(N) = O(N/2) + O(1) \\ => T(N) = (log_2 N)}$$

The space complexity is O(1) as it runs without any extra spaces.

Here is the comparison between Linear Search and Binary Search.

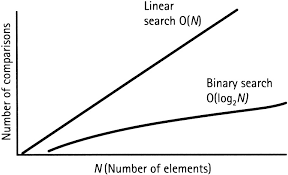
Hope you find it helpful. Subscribe to the newsletter for more content like this.