ML - Day 19 | UNSUPERVISED LEARNING | Principal Component Analysis (PCA) 🌸😊

Clustering Plant Iris Using PCA🌷🌼

Step 1: Find Problem 🔎

• Categorizing Iris Data into 'setosa' 'versicolor' 'virginica'

• 

Step 2: Collect Dataset 🛒

• Leaf Iris data analysis and segregate data into different categories.

• Import the iris dataset from sklearn library

• Input : Plant Iris Data

Step 3: Segregate Dataset into X and Y 🎭

• Segregation Data

  • X = dataset.data

  • Y = dataset.target

• Summarize data.

  • Shape

  • Describe

Step 3: Algorithm | Principal Component Analysis ⚓

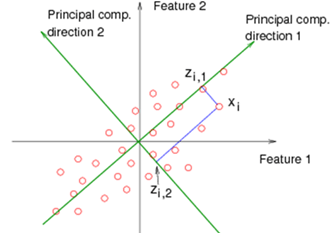
Definition :

• Dimensionality-reduction method.

• That is often used to reduce the dimensionality of large data sets,

  • by transforming a large set of variables into a smaller one

  • that still contains most of the information in the large set.

Step :

• Standardization :

  • All the variables need to be transformed to the same scale.

  • Otherwise, some high input features will contribute a lot to output.

  • 

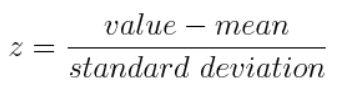
• Covariance :

  • How the input data variables vary from the mean with respect to each other.

    • Relationship between each other features.

      

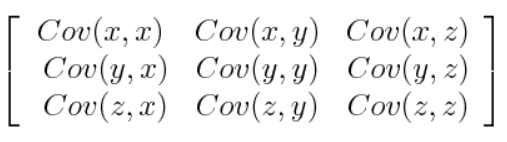
  • Conditions :

    • (+)ve - Two variables increase or decrease together. **Correlated**

    • (-)ve - One increases when the other decreases. **Inversely correlated**

• Eigen Values & Eigen vectors

  • To find the Principal Components,

    • Eigen Values & Eigen vectors need to be computed

      • on the covariance matrix

  • Principle Components

    • New variables are constructed as linear combinations or mixtures of the initial variables.

    • Computing the eigenvectors and ordering them by their eigenvalues in descending order.

    • Eg:

      • 10-dimensional data gives you 10 principal components,

      • but PCA tries to put the maximum possible information in the first component,

      • then maximum remaining information in the second and so on.

      • Output:

        

  • Eigen Vector

    • Directions of the axes where there is the most variance(most information)

  • Eigen Values

    • Amount of variance carried in each Principal Component

• Feature Vector

  • Where dimension reduction starts.

  • To choose whether to keep all these components or discard those of lesser eigenvalues to form a matrix with the remaining ones.

    • Feature Vector - Both eigenvectors

      

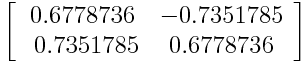
    • Feature Vector - Only one Eigenvectors

      

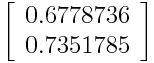
• Recasting Data along the axes of Principal components

  

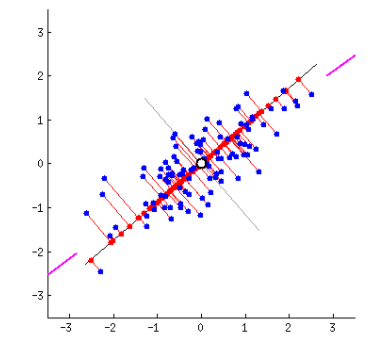
  • Reorient the data from the original axes to the ones represented by the principal components.

  • Formula - PCA

    • Final Dataset = [Feature Vector]^T * [Standardized Orginal Dataset]^T

Step 4: Fitting the PCA clustering 🛠

• To the dataset by specifying the Number of components to keep.

• Git Repo: link

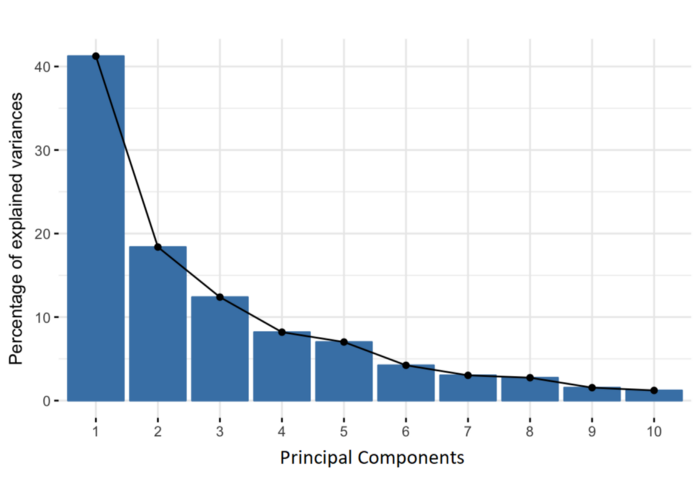
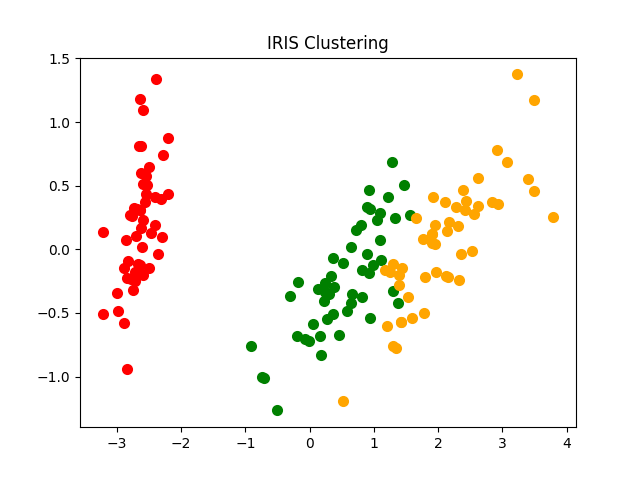
Step 5: Clustering via the Variance Percentage 💐

Screenshot for Output of Iris Clustering :

Thank you for joining me on this adventure 🛫. Don't forget to stay tuned for more exciting updates and discoveries 🧡. Let's continue to dive into the world of ML and embrace its magic to shape a brighter future for software development!

Until next time,

Sarangi❤