A Simplified view of Disjoint Set

Introduction

The disjoint set data structure is a form of data representation majorly used to solve problems that have to do with connectivity. It maintains a collection of disjoint subsets. It has many applications in real life such as social networking, games, least common ancestor, etc.

Consider a huge riverine area 'X'. The area is so water-logged that sometimes, to visit the immediate next village there might not be a path on land leading to it, and one might have to use a boat to get there. The problem now is that, in this area, it was reported that in the past 4 days, all the villagers who tried using boats to get across to a neighbouring village got eaten by crocodiles. Due to this issue, the leaders of the villages in the area gathered together and banned the use of boats. They agreed to raise funds to build a road network utilising bridges to go over rivers. In the meantime, they provided a basic app for the road network to the villagers and all people living in that area which they could use to check if they could get to another village from a source village (that is, they use it to check the status and progress of the road network). So this app basically receives 2 inputs from users: source village and destination village. It then returns an output which could be 'Yes' (there is a path leading from the source village to the destination village through the network) or 'No'. Also, it has an interface for admins, where they can provide 2 villages to be marked as 'connected', that is, the admin uses this feature to indicate that a bridge has just been built between two villages. The question now is: how does this system/app work?

This is where the Disjoint Set data structure comes in handy. It provides 2 primary operations: union; for connecting 2 items and find; for finding the subset to which an item belongs, where each subset is uniquely identified by its 'root' (don't worry, you will get the concept of the 'root' as you read along). The developer of the app makes available, an instance of the disjoint set structure and anytime a new bridge is built, the admin passes the 2 villages that the bridge connects to the provided interface and the union method of the disjoint set is called under the hood. It keeps doing this for any bridge built. As a user, anytime I query the app, passing in a source and destination village, under the hood, the system invokes the find method twice, first, on the source village and second, on the destination village. If they return the same result (they are in the same subset), then there is a path between them and it returns 'YES', otherwise it returns 'NO'.

As for the term “connectivity”, note that it is an equivalence relation, that is, it is symmetric, reflexive and transitive, i.e., symmetric: if village 'A' is connected to 'B', then village 'B' is connected to village 'A'; reflexive: every village is connected to itself; transitive: if village 'A' is connected to village 'B', and B is connected to village 'C', then village 'A' is connected to 'C'.

Modelling a sample problem

Under the hood, the Disjoint Set data structure makes use of an array, however, it is best we apply a tree-like model to the linear structure(array) because connectivity isn’t usually linear in the real world.

To get a sound understanding, let’s try to model a road network system (as discussed earlier) of 8 villages (A, B, C, D, E, F, G, H) where each village is connected to at least one village, i.e., if a village is not connected to any other village, it must at least, be connected to itself (based on the reflexive property of connectivity). Here, we map the 8 villages to integers ranging from 0 to 7 {A -> 0, B -> 1, C -> 2, D -> 3, E -> 4, F -> 5, G -> 6, H -> 7}.

We initialise an array for this and set the values of the array to correspond with their index as shown below. Here, the village at index i represents the parent of village i, and as such, is connected. The interpretation is that initially, no bridge has been built, therefore, each village is only connected to itself and are all roots (from a tree point of view).

What we gave above is a linear model of the system. Let’s apply a tree-like model to the linear structure

As can be seen above, each village is connected only to itself, and the non-linear structure is made up of 8 trees where each tree is only made up of its root. For instance, village 0 is only connected to itself, and it is the root of the first tree.

Note: Starting from this point, we will not show the reflexive connection (relationship between an item and itself) in our tree-like models to simplify the view.

Now, let’s see what we can build with this. Let’s connect village 0 and village 2. Two villages are said to be connected if and only if they have the same root (in the same subset), i.e., if they are a component of the same subset/tree.

The question is how do we connect 2 villages? Well, we follow the steps below

1. Trace the root (not parent) of the first village's tree

2. Trace the root of the second village's tree

3. If the roots are the same, then return, because they are already connected. Otherwise

4. Merge the shorter tree into the taller tree if they are of unequal heights, otherwise, just merge the second tree into the first (or first into the second). For the sake of this article, we will always merge the second tree into the first tree when the trees are of equal height.

The above steps were given in terms of the tree-like model of the underlying linear structure. So, how would we implement it using the actual array? First note the following,

• the parent of village i (where i is an integer) is arr[i]; the grandparent of village i is arr[arr[i]]; the great grandparent is arr[arr[arr[i]]] and so on.

• to trace the root of a village represented by a given index, we keep tracking the parents, grandparents, great-grandparents, etc., until one of them eventually turns out to be a root.

• we only encounter a root in the array when a given value in the array is equal to its index. Therefore, the number of trees in a given array is the number of items whose value equals its index.

• We merge the tree containing village a with root i (where arr[i] == i) into the tree containing village b with root j(where arr[j] == j) by setting arr[i] = j ( arr[i] no longer equals i, hence the condition for i to be a root no longer holds. Instead, i with all its associated children becomes a child of item j which leaves j as the root of village a and village b)

• we have made mentions of merging the shorter tree into the taller tree, but how do we know a tree is taller than another? Well, we will keep an extra array with which we would keep track of the height of each tree. Check the code implementation to understand better.

So, based on the points we provided above, we can now apply the steps stated for our tree-like model to the underlying linear structure (array).

Simulation of the problem

Now let’s go back to our problem of the real-world system consisting of 8 villages.

Underlying linear structure (array)

height array to hold the height of individual trees

Tree-like model

---

Connecting the item 0 and item 2, we

1. Trace the root of item 0, which is itself (village 0)

2. Trace the root of item 2, which is itself (village 2)

3. is 0 == 2? No, hence we merge the trees into 1 tree

4. They are of equal height, so I would set arr[2] = 0

Let’s now have a visual representation of our structures.

Underlying linear structure (array)

height array to hold the height of individual trees

Tree-like model

---

Let’s do a few more connections. Let’s connect villages 4 and 5. Also, let’s connect villages 3 and 7.

Following the steps given earlier to connect two villages, we would arrive at the following

Underlying linear structure (array)

height array to hold the height of individual trees

Tree-like model

---

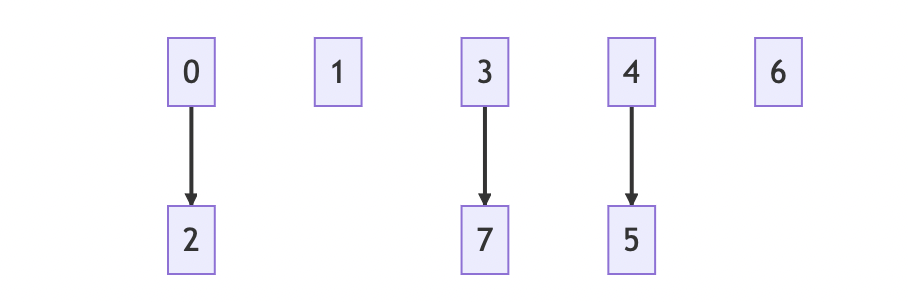
All the above connections have been between two villages whose tree length are equal. Let’s now attempt to connect two villages with their trees having different lengths. Here, we aim to connect villages 1 and 7.

Let’s go over the steps

1. Trace the root of village 1. Here the root is itself, i.e., item 1.

2. Trace the root of village 7.

   — It is not its own root because arr[7] !== 7 . So, we must trace its root by following its parent, grandparent, etc., until one turns out to be its own root. That would then be the root of village 7. Let’s go.

   • village 7’s parent is arr[7] which is equal to 3.

   • village 3’s parent (village 7’s grandparent) is arr[3] which is equal to 3.

   • Hurray, we have traced village 7 to its root because we have found a forbear of 7, such that arr[i] == iis true (arr[3] = 3)

   • Therefore, the root of village 7 is 3 (item 3)

3. Are the roots equal? NO. 1 ≠ 3. Move to step 4

4. check the height array to get the height of the trees of which villages 1 and 3 are roots. The height of village 1's tree is 0, while the height of village 3's tree is 1. Therefore, the tree that has village 3 as its root is the taller tree, hence we merge the first tree (tree that has village 1 as its root) into the second tree by setting arr[1] = 3 . 3 then becomes the root of village 1

Let’s have a visual representation.

Underlying linear structure (array)

height array to hold the height of individual trees

Tree-like model

---

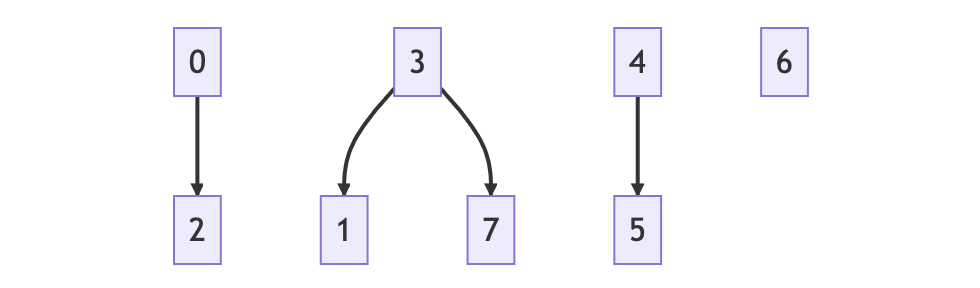
Currently, we can see that we have 4 different subsets which are all disjoint: { {0, 2}, {1, 3, 7}, {4, 5}, {6} }. Therefore, it is not currently possible to move from from village A (0) to village E (4) because they are not in the same subset, that is, there is no path between A and E.

More connections can be made, and we can always query the data structure to find out the connection status of two given items.

Implementation in Java

public class DisjointSet {

    private int[] items;
    private int[] size;

    public DisjointSet(int n) {
        items = new int[n];
        for (int i = 0; i < n; i++) items[i] = i;
        size = new int[n];
    }

    private int root(int item) {
        while (items[item] !== item) {
            // path compression
            //items[item] = items[items[item]];
            item = items[item];
        }
        return item;
    }

    public int find(int item) {
        return root(item);
    }

    public void union(int item1, int item2) {
        int rootItem1 = root(item1);
        int rootItem2 = root(item2);
        // weighting
        if (size[rootItem1] > size[rootItem2]) items[rootItem2] = rootItem1;
        else if (size[rootItem2] > size[rootItem1]) items[rootItem1] = rootItem2;
        else { 
            items[rootItem2] = rootItem1;
            size[rootItem1]++;
        }
    }

}

Conclusion

Further optimisations could be made to make this data structure more efficient. For instance, we could compress the paths each time we try to query the root of a village/item by setting items[item] = items[items[item]]. This will greatly reduce the height we need to travel to find the root. However, it should be noted that the height array should keep track of this 'compression' so that the optimisation works as expected.

In this article, we gave a trivial example of a road network connecting villages. The disjoint set data structure can do way more with little modifications and additions. The reader can check out more about its application on the internet and see if it has a use in their current or even future projects.