No-Cloning Theorem in Quantum Computing

In the intricate realm of quantum mechanics, where particles are analyzed using probability and uncertainty, there exists a fundamental principle that challenges our classical intuition - the No Cloning Theorem. As we delve into the mysterious world of subatomic particles and the laws that govern their behavior, we are confronted with the profound notion that copying quantum information is not as straightforward as photocopying a document in the classical world.

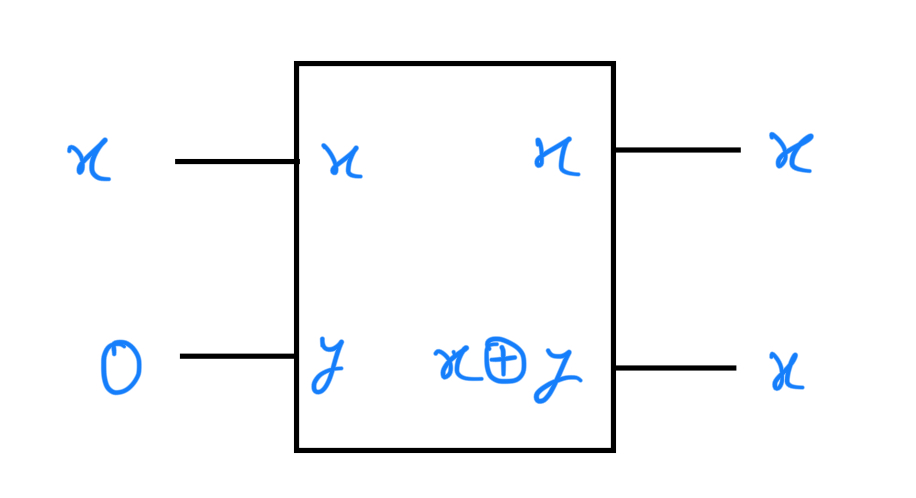
At the heart of comprehending the No-Cloning Theorem lies a crucial gateway: the CNOT gate. In the classical realm, the act of copying a classical bit is facilitated by a classical CNOT gate. This gate, depicted in the figure below, operates by taking an input bit in an unknown state 'x' and a 'scratchpad' bit initialized to zero. The outcome of this process yields two bits, both residing in the identical state 'x'.

Suppose a qubit is in an unknown state given by:

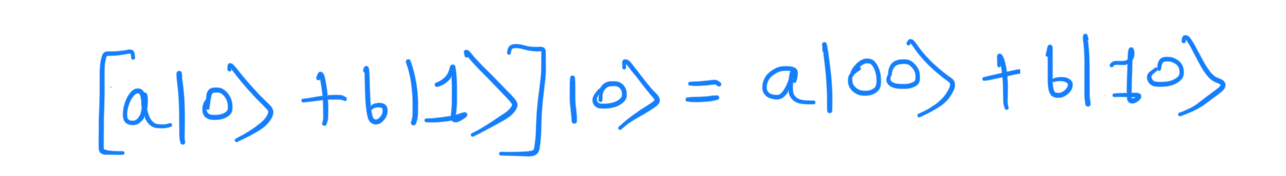
We try to copy the qubit in the same manner by using a CNOT gate. The input state of the two qubits may be written as:

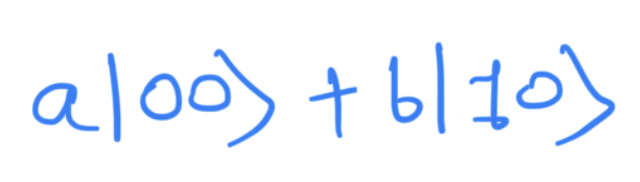
Applying the CNOT gate to the input state:

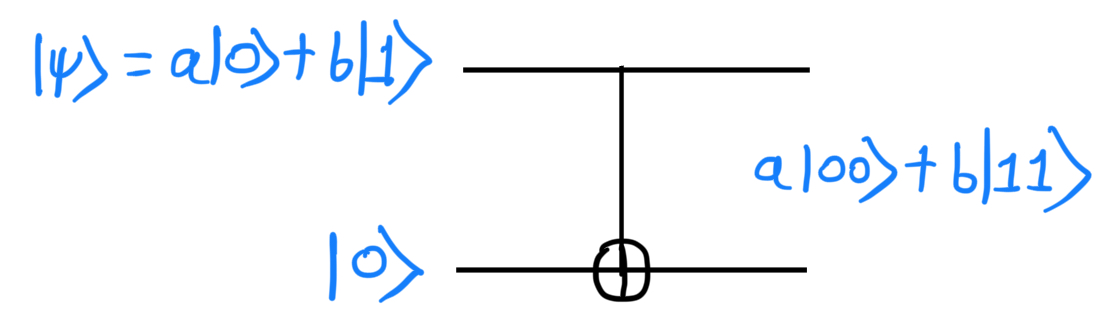
The function of CNOT is to negate the second qubit when the first qubit is 1, and thus the output is simply:

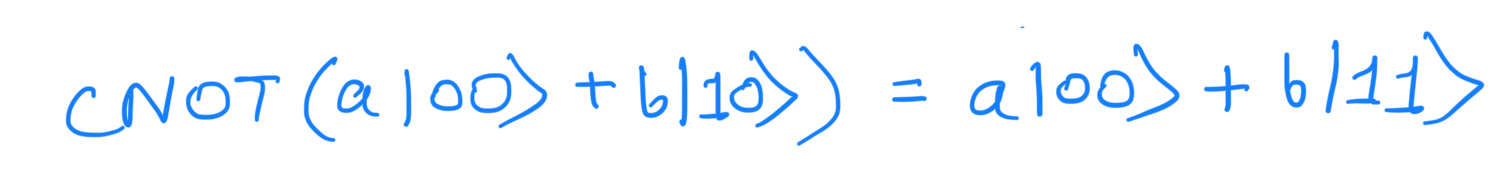
Have we successfully copied the state |Ψ⟩? i.e. have we created the state |Ψ⟩|Ψ⟩? It is possible to use quantum circuits to copy classical information i.e. |Ψ⟩=|0⟩ or |Ψ⟩=|1⟩. However, for a general state(classical and quantum), we see that:

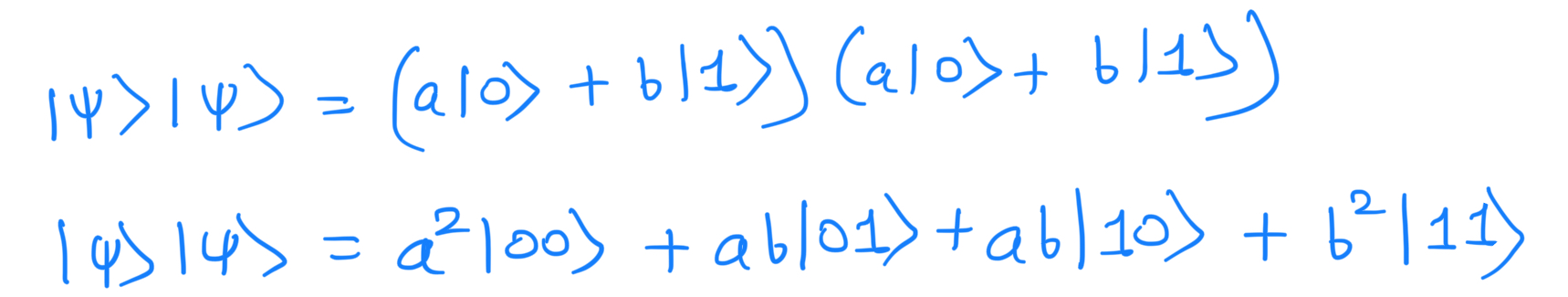
Equating the output:

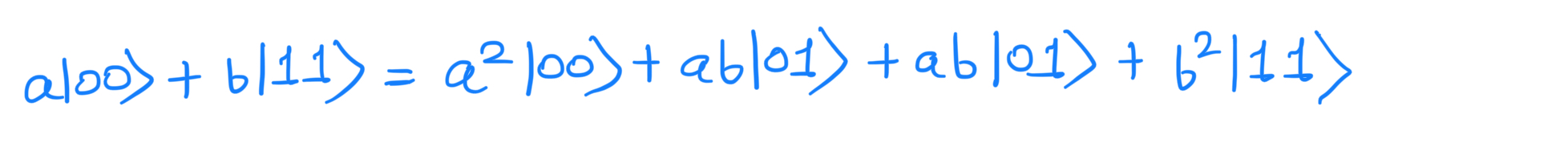
Unless ab=0 the 'copying circuit' above does not copy the quantum state. It turns out to be 'impossible' to make a copy of an unknown quantum state. This property, that qubits cannot be copied, is known as the No-Cloning theorem and it is one of the chief differences between quantum and classical information.

Understanding the intuition of the No-Cloning theorem in terms of measurement:

There is another way of looking at the failure of the circuit based on the intuition that the qubit somehow contains 'hidden' information not directly accessible to measurement. If we measure one of the qubits of the state a|00⟩+b|11⟩ we obtain either 0 or 1 with probabilities

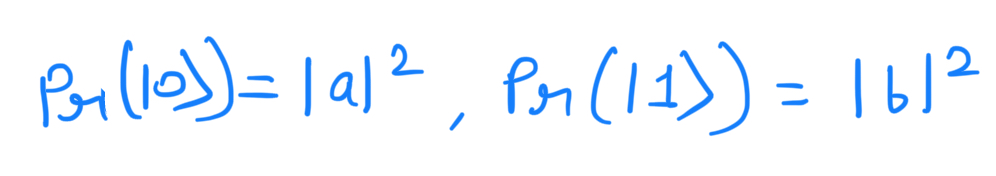
However, once one qubit is measured, the state of the other one is completely determined, and no additional information can be gained about a and b. In this case, the extra hidden information carried in the original qubit |Ψ⟩ was lost in the first measurement and cannot be regained. If, however, the qubit had been copied, then the state of the other qubit should still contain some of that hidden information. Therefore a copy cannot be created.

Proof of No-Cloning Theorem:

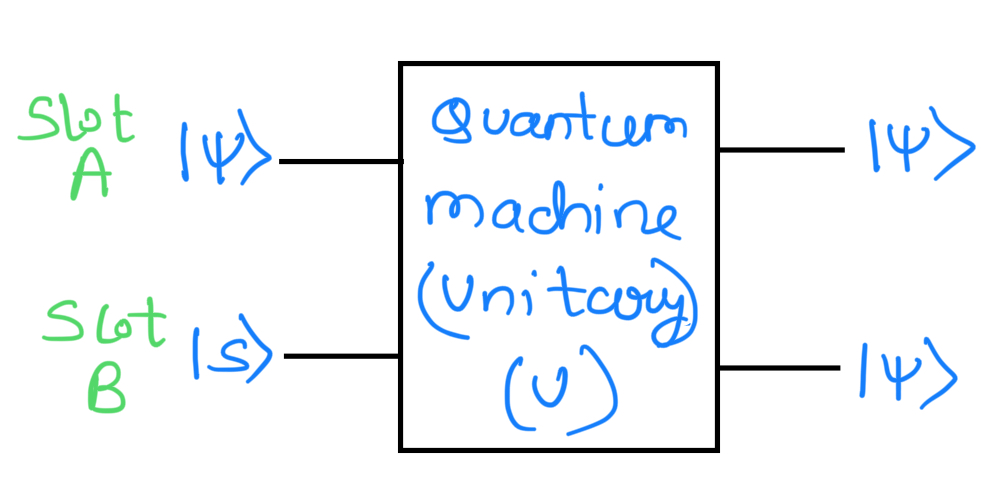
Suppose, we have a quantum machine with two slots A and B. Slot A is the data slot and it starts in an unknown but pure quantum state |Ψ⟩. This is the state which is to be copied into slot B which is the target slot. Thus the initial state of the copying machine is given as:

Some unitary evolution U now affects the copying procedure, ideally,

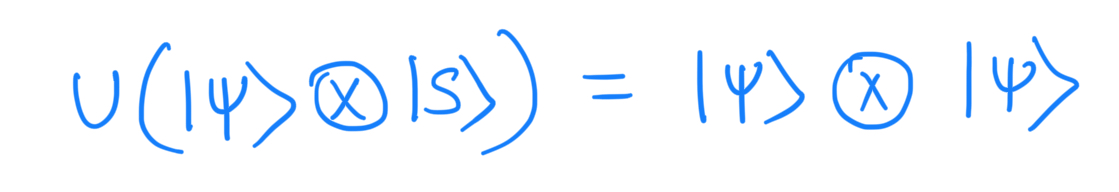
Suppose this copying procedure works for two particular pure states |Ψ⟩ and |φ⟩. Then we have:

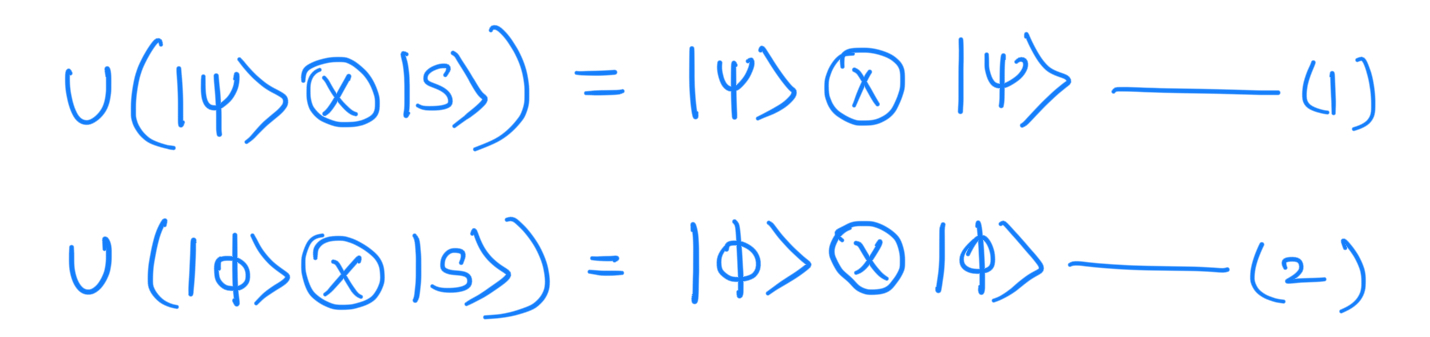
Taking the transpose-conjugate of the first equation we get:

---

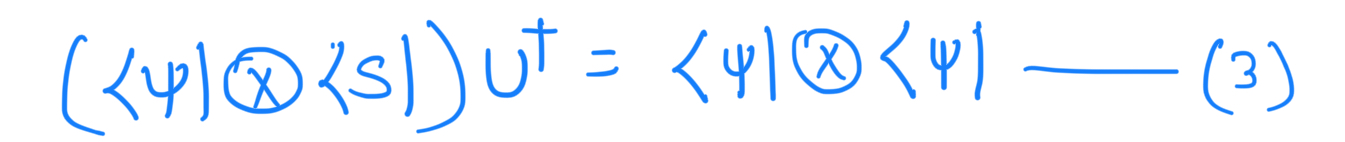
Note:

1)The inner product of two tensor products is given as follows:

2)If |i⟩ and |j⟩ are two orthogonal vectors then the following are the inner product values:

---

Now taking the inner product of equations (2) and (3):

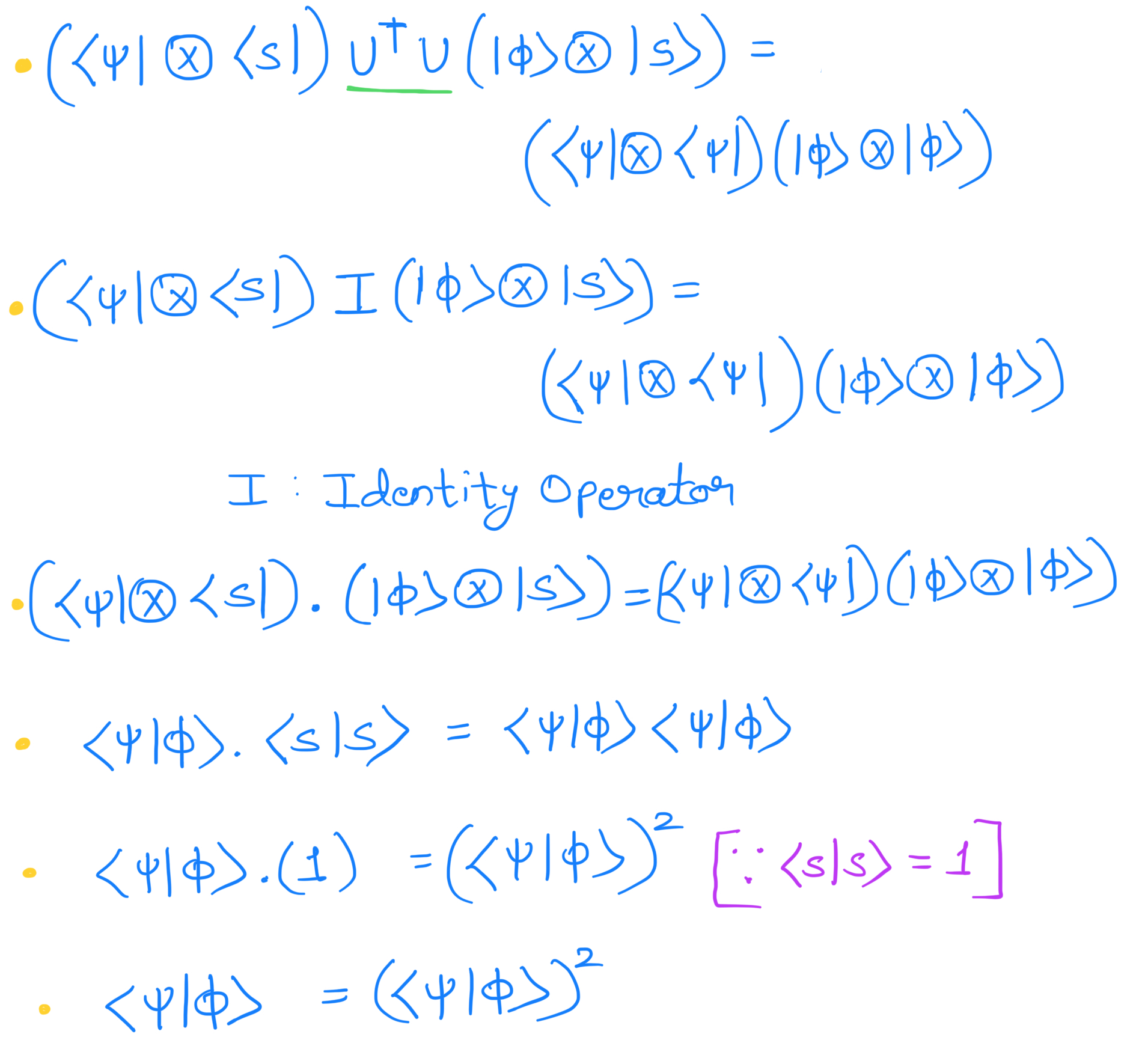
Now the above equation is as follows:

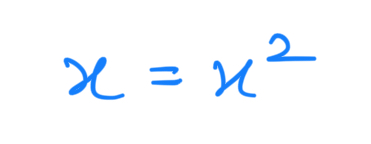
It has the following two solutions:

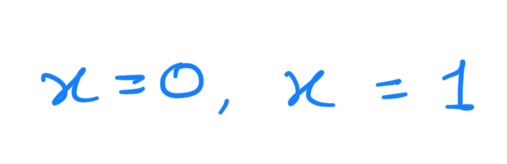
Hence:

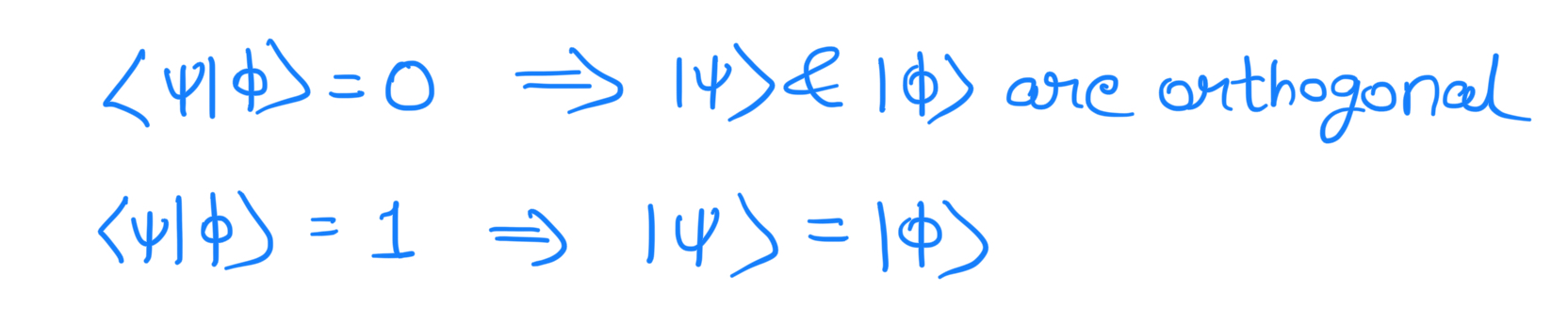
Thus a cloning device can only clone states, which are orthogonal to one another, and therefore a general quantum cloning device is impossible. Hence it is impossible to clone the following quantum states with the same cloning device:

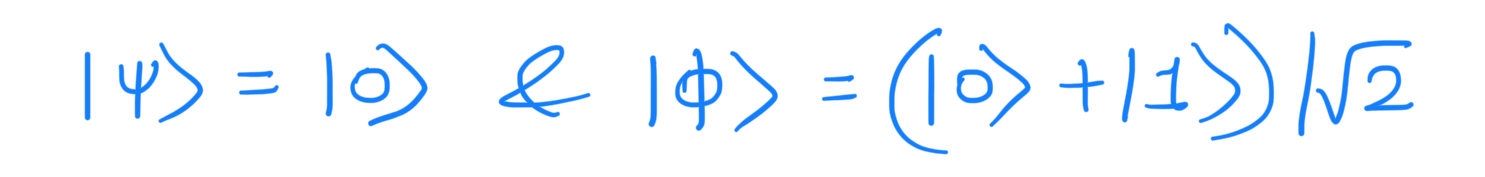
Hence we have shown that it is impossible to perfectly clone an unknown quantum state using unitary evolution. The cloning of non-orthogonal pure states remains impossible unless one is willing to tolerate a finite loss of fidelity in the copied states.

Credit for the above blog:

I have gained the information for the above blog from the book "Quantum Computing and Quantum Information" by Michael A. Nielsen and Isaac L. Chuang.