Algorithm Analysis
 Xander Billa
Xander Billa
For every algorithm we write and implement data structure using different methodologies but to consider which methodology is best we need to compare and that comparison is nothing but analysis of algorithm.
Analysis of algorithm can be done in two ways -
1. Space complexity:
Additional space (Number of elements is stored) required to run a programme is called Space Complexity.
It wouldn't include Space occupied by inputs.
It is the space that is required while executing the programme. The output of the algorithm can be included in space complexity, if it takes more than desired space.
2. Runtime complexity:
Time required to run the algorithm is called Runtime Complexity. Item measuring two ways -
On clock time: In this it measure the time in nanosecond or second for each execution.
But it changes frequently for every time we run the programme because the wall clock time depends on various factors of operating system such as interrupt generated background processes, hardware connected peripheral devices interrupt etc.
Number of operations: In this runtime complexity is measured in terms of number of operations required to complete the execution of the program.
Here the runtime complexity will depend on the number of inputs so it will be written in some standard form in terms of
n.
For every algorithm there are two types of cases in terms of time complexity-
Best Case: The type of input for which algorithm takes minimum time.
Worst Case: The type of input for which algorithm maximum time.
Rate of Growth
With what rate runtime complexity increases with increment in input size.
| Number of Inputs | Number of steps |
| 4 | 6 |
| 15 | 17 |
| 200 | 202 |
n | n+2 |
The runtime complexity for above will be - T(n) = n + 2
So, we can say that the runtime complexity is increasing linearly. Following up some complexity, depend on the rate of growth.
| Rate of Growth | Complexity |
| Constant | 1 |
| Logarithmic | log n |
| Linear | n |
| Logarithmic linear | n log n |
| Quadratic | n2 |
| Cubic | n3 |
| Exponential | 2n |
Asymptotic Notation
A mathematical representation to represent the time space complexity is called asymptotic notation.
Basically it is of three types -
Big O Notation (O)
Define an upper bound of an algorithm.
It gives non-negative
f(n)andg(n)defines on a positive integer so we can say thatf(n) = O(g(n))Is there exists a positive integer n0 and positive constantCsuch that -f(n) ≤ C . O(g(n)) ∀ n >= n0i.e., growth rate ofg(n)should be greater thanf(n).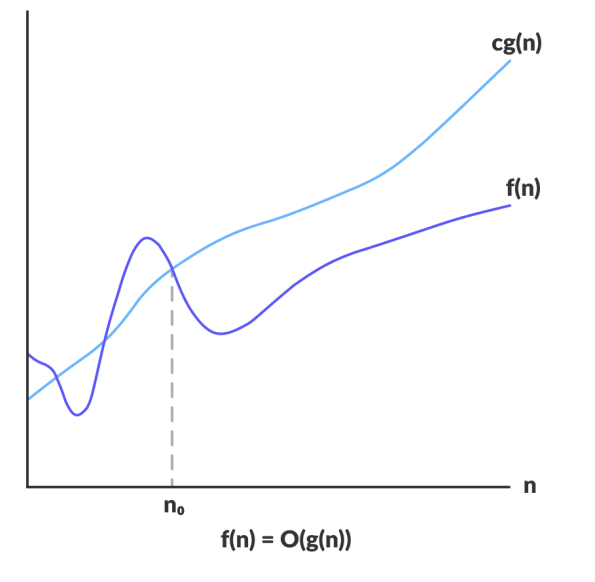
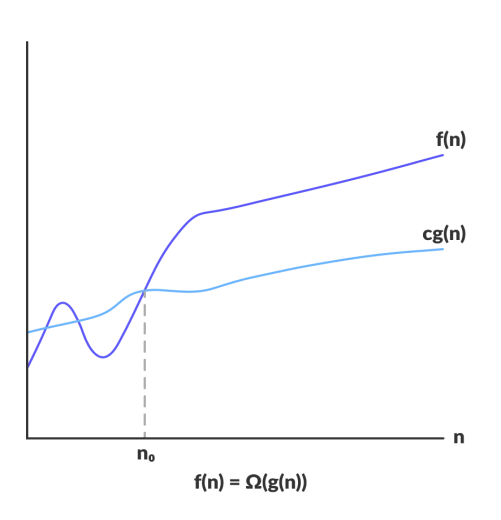
Omega Notation (Ω)
Define an lower bound of an algorithm.
It gives non-negative
f(n)andg(n)defines on a positive integer so we can say thatf(n) = Ω(g(n))Is there exists a positive integer n0 and positive constantCsuch that -f(n) ≥ C . Ω(g(n)) ∀ n >= n0i.e., growth rate ofg(n)should be less thanf(n).
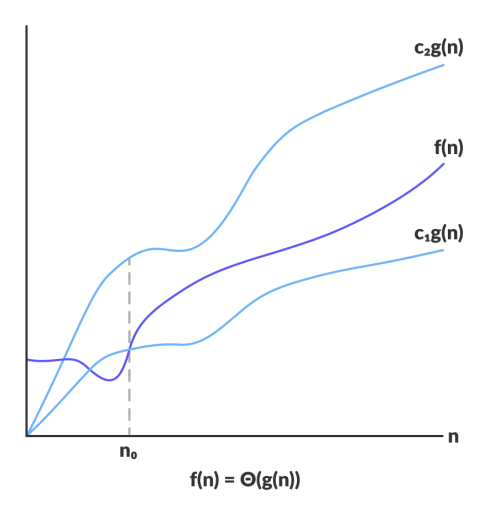
Theta Notation (θ)
Provide asymptotic equal bound.
It gives non-negative
f(n)andg(n)defines on a positive integer so we can say thatf(n) = θ(g(n))Is there exists a positive integer n0 and positive constantC1andC2such that -C1 . θ(g(n)) ≤ f(n) ≤ C2 . θ(g(n)) ∀ n >= n0i.e., growth rate off(n)should be equal tog(n).
Examples
Example 1 -
for (i = 0; i <= n; i++){
x = m + 2;
}
So the runtime complexity for the above example will be -
| Statement | Rate of growth |
for (i = 0; i <= n; i++) | n + 1 |
x = m + 2 | n |
| Total Complexity | 2n + 1 (Linear) → θ(n) |
Example 2 -
for (i = 0; i <= n; i++){
for (j = 0; j <= n; j++){
x = m + 2;
}
}
So the runtime complexity for above programme will be
| Statements | Rate of growth |
for (i = 0; i <= n; i++) | n + 1 |
for (j = 0; j <= n; j++) | n (n + 1) |
x = m + 2 | n * n |
| Total Complexity | 2n2 + 2n + 1 (Quadratic) → θ(n<sup>2</sup>) |
Example 3 -
for (i = 0; i <= n; i++){
for (j = 0; j <= n; j++){
for (k = 0; k <= n; k++){
x = m + 2;
}
}
}
So the runtime complexity for above programme will be -
| Statements | Rate of growth |
for (i = 0; i <= n; i++) | n + 1 |
for (j = 0; j <= n; j++) | n (n + 1) |
for (k = 0; k <= n; k++) | n ( n ( n + 1)) |
x = m + 2 | n x n x n |
| Total Complexity | 2n3 + 2n2 + 2n + 1 (Cubic) → θ(n<sup>3</sup>) |
Example 4 -
for (i = 0; i <= n; i=i*2){
x = m + 2;
}
So the runtime complexity for above programme will be -
| Statements | Complexity |
for (i = 0; i <= n; i=i*2) | log 2 N |
x = m + 2 | n |
| Total Complexity | n log 2 N (Linear) → θ(n log 2 N) |
Example 5 -
for (i = 0; i <= n; i=i*2){
for (j = 0; j <= n; j=j*2){
x = m + 2;
}
}
So the runtime complexity for above programme will be
| Statements | Rate of growth |
for (i = 0; i <= n; i=i*2) | log n |
for (j = 0; j <= n; j=j*2) | log n * log n |
| Total Complexity | log n ( log n * log n ) → θ(log 2 n)<sup>2</sup> |
Example 6 -
for (i = 0; i <= m; i++){
a = a + sqrt(i);
}
for (j = 0; j <= n; j++){
b = b + sqrt(j);
}
So the runtime complexity for above programme will be
| Statements | Rate of growth |
for (i = 0; i <= m; i++) | m |
for (j = 0; j <= n; j++) | n |
| Total Complexity | n + m → θ(m + n) |
Example 7 -
for (i = 1; i <= n; i++){
for (j = 1; j <= i; j++){
x = m + 2;
}
}
So the runtime complexity for above programme will be
| Statements | Rate of growth |
for (i = 0; i <= m; i++) | n |
for (j = 0; j <= i; j++) | for i = 1 loop will run 1 times, |
for i = 2 loop will run 2 times,
for i = 3 loop will run 3 times,
.
.
.
for i = n loop will run n times,
So, it will be -1 + 2 + 3 + . . . + n = (n (n + 1)) / 2 = (n<sup>2</sup> + n) / 2 |
| Total Complexity | ((n2 + n) / 2 ) + n → θ(n<sup>2</sup>) |
Conclusion
In algorithm analysis, understanding space and runtime complexities through Big O notation helps assess efficiency. Examples illustrate complexities like linear, quadratic, and logarithmic, aiding algorithm optimization.
Subscribe to my newsletter
Read articles from Xander Billa directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Xander Billa
Xander Billa
Myself Vikas Singh from Varanasi, Uttar Pradesh. Learning and exploring technical domains at Acharya Institute, Bangalore (IN) from the last two years. The main goal is to learn as much domains, tool